類似ベクトル検索のSoTA！！GCP: Vertex Matching Engineにも使用されている手法ScaNNを紹介！

vector search 2021年06月04日

3つの要点
✔️ GCPの新プロダクト「Vertex Matching Engine」の元論文
✔️ MIPSスコアを考慮した新しい量子化損失関数を提案
✔️ ANNBenchmarksでSoTA性能を記録

Accelerating Large-Scale Inference with Anisotropic Vector Quantization
written by Ruiqi Guo, Philip Sun, Erik Lindgren, Quan Geng, David Simcha, Felix Chern, Sanjiv Kumar
(Submitted on 27 Aug 2019 (v1), last revised 4 Dec 2020 (this version, v5))
Comments: Published as a conference paper at ICML 2020.
Subjects: Machine Learning (cs.LG); Machine Learning (stat.ML)

code：

はじめに

ScaNNはGoogleが発表した、類似ベクトル検索の高速化を目的とし、有名なベンチマークサイト"ann-benchmarks.com"でも最先端の性能を記録している手法です。先日、GCPにVertex Matching Engineという類似ベクトル検索をすごいパフォーマンスで実現するプロダクトがリリース（プレビュー版）されていましたが、ここにも使われている技術となります。注目度も高いプロダクトであるため、この機に元論文の紹介をしてみようと思います。

類似ベクトル検索はすごく多様なサービスに応用でき、機械学習ともよく組み合わせて使用されている一方で、個人的には、有名なサービスやライブラリを利用したとしてもパフォーマンス面ではまだ課題が残っているのが現状だと思っていました。しかし、Vertex Matching Engineのドキュメントを眺めてみるとものすごいデータ規模とQPSに耐えられるという記述があるため、その意味も込めてVertex Matching Engineは個人的に期待しているプロダクトです。

類似ベクトル検索

類似ベクトル検索（最近傍探索とも呼ばれる）は、大規模な分類・検索タスクを解決するための一般的な手法として用いられています。特に、機械学習モデルによりデータを埋め込み空間に写像することで、従来では困難だった抽象的なクエリに答えられるようになったため、非常に汎用的な技術となっています（下のgifのようなフロー）。例えば、類似商品、類似画像、類似文書のレコメンドなどへの応用が考えられます。

最近傍探索を実現する一般的な手法としては、内積距離を使ったMaximum inner product search（MIPS）があります。MIPSの問題を正式に定義すると次のようになります。

$n$個のデータポイントを持つデータベース$X={x_i}, i=1,2,...,n$を考えます。各データポイント$x_i \in R^d$は$d$次元のベクトル空間にあります。ここで、クエリ$q \in R^d$が与えられた時、$q$との内積が最も大きいデータポイント$x \in X$、すなわち以下を特定することです。

$$x_i^* := arg max \left< q, x_i \right>$$

ここで、データベースは通常大規模なものになるため、クエリ$q$と全てのデータポイントとの内積を網羅的に計算することは現実的でない場合が多いです（データ数$N$、ベクトルの次元数$d$とすると$\mathcal{O}(Nd)$）。そのため、厳密に最近傍のデータ点ではなくとも、検索を高速化した近似最近傍探索が一般には使われており、ハッシュ化、グラフ探索、量子化等に基づく技術が様々な研究で提案されています。

MIPSの効率化

効率的なMIPSシステムを開発するためには、主に以下の2つの課題があります。

クエリとの比較を行うデータポイントの数を減らすこと
- 木構造、グラフ、（類似性を保持する）ハッシュ関数による空間分割などの方法がある
- 与えられたクエリに関連する部分空間内のデータのみと比較する
データポイントの圧縮
- ベクトル量子化による手法が最先端
- 圧縮により、内積にかかる計算量削減、メモリ使用量削減によるリソース効率の向上、ストレージ削減など、様々な利点

これらの課題に対処するために、上述のような様々な手法が提案されています。著者らの貢献は量子化の部分であり、速度面だけでなくMIPSの精度も考慮した量子化損失関数を提案したところが新しい点になります。

以下ではまず量子化について説明を記載していますが、すでにご存知の方は著者らの提案手法の部分まで読み飛ばしていただいても構いません。

ベクトル量子化

ベクトル量子化の一般的な手法である直積量子化を例として取り上げ、量子化における基本的な考え方・手順を簡単に説明すると、以下のような流れになります。

（事前準備）コードブックを構築
- ベクトルを$M$分割し、$M$個の$d/M$次元ベクトルとして考える
- データベースのデータポイントにk-meansを施し求める
（事前準備）コードブックを利用してデータベースの全データ点を量子化
- float型の$d$次元ベクトルから、uint型の$M$次元ベクトルに圧縮される
- $32 \times d$ bit $\rightarrow$ $8 \times M$ bit
（クエリ時）クエリデータを量子化し、データベースのPQコードから探索

クエリベクトルが与えられた時の量子化のイメージは下図のようになります。なお、このステップではクエリと各コードワードとの距離表も記録しておきます。

東京大学の松井先生のチュートリアル資料を参考(ぜひ、こちらもご確認ください。)

また、量子化後は全ステップで計算された距離表を使いながら、データベースのPQコード群から距離が最も近いものを線形探索します。

これにより、元々$\mathcal{O}(Nd)$かかり、規模が大きいと現実的でなかった探索問題が、$\mathcal{O}(dK + MN)$というはるかに少ない計算量で実現可能にしています。

コードブックの構築

ここでは事前準備であるコードブックの構築について説明します。コードワードの選択における最適化問題をは、定式化すると以下のようになります。

$$min_{c_1, c_2, \cdots, c_k \in \mathbb{R}^d} \sum_{x_i} min_{\tilde{x_i} \in \{c_1, c_2, \cdots, c_k\}} ||x_i - \tilde{x_i}||^2$$

これは実はk-meansにおいて解く最適化問題と全く同じ形式でもあり、k-meansと同様のアルゴリズムで求めることができます。下記にコードブックの作成手順を示しています。

（初期化ステップ）コードワード$c_1, c_2, \cdots, c_k$を$x_1, \cdots, x_n$からサンプリングしたランダムなデータポイントとして初期化する
（パーティション割り当てステップ）各データポイント$x_i$に対して、距離の近いコードワード$\tilde{x_i}$を見つける
- $$\tilde{x_i} = arg min_{\tilde{x_i} \in c_1, \cdots, c_k} l(x_i, \tilde{x_i})$$
（コードブックの更新ステップ）$\hat{x_i} = c_j$となるすべてのデータポイント$x_i$を$X_j$と置いたとき、各コードワード$c_j$を下式により更新する
- $$c_j \leftarrow arg min_{c \in \mathbb{R}^d} \sum_{x_i \in X_j} l(x_i, c)$$
収束するか、最大反復回数に達するまで、ステップ2とステップ3を繰り返す

各反復において、コードワードごとに更新ステップを行う必要があります。ここでは簡略化のため、ベクトルの分割を想定せずに説明してますが、直積量子化の場合にも同じような手順で求めることが可能です。

また、一般的な量子化技術に使用されている距離関数$l$は、データポイント$x$を$\tilde{x}$に量子化した時の再構成誤差を最小化することに焦点を当てています。

空間分割

ベクトル量子化においても、エンコードの仕方を工夫することで空間分割と同様の効果も得られます。例えば、k-meansと同じように以下のようなボロノイ空間分割を考えることができます。

クエリベクトルの対応するコードワード領域が確定すると、そのコードワードとの距離の残差$r_q=q-c_i$を量子化し、記録しておくという考え方になります。これにより、クエリはデータベース全体ではなく、同じ空間内のデータ点のみを比較すれば良いことにもなるため、効率性が向上します。

規模にもよりますが、ベクトル量子化というとこういったメカニズムで行われるのが主流になってきていると思われます。

提案手法：ScaNN

それでは提案手法の説明に入ります。著者らは最終的な目的であるMIPS精度（検索精度）の向上を考慮した異方性量子化損失関数という新しい目的関数を提案することで、ANN-Benchmarksの最先端の性能を記録しています。

既存のベクトル量子化は、量子化の際の再構成誤差の最小化を目的関数として学習していると述べました。これはMIPSの文脈からすると中間目標のように感じられますが、これ自身がMIPS精度を無視して設計されているかというと実はそうではありません。

$$\mathbb{E}_q \sum_{i=1}^n (\left< q, x_i \right> - \left< q, \tilde{x_i} \right> )^2 = \mathbb{E}_q \sum_{i=1}^n \left< q, x_i - \tilde{x_i} \right>^2$$

$$\sum_{i=1}^n \mathbb{E}_q \left< q, x_i - \tilde{x_i} \right>^2 = \sum_{i=1}^n \mathbb{E}_q (x_i - \tilde{x_i})^Tqq^T(x_i - \tilde{x_i}) = c\sum_{i=1}^n||x_i - \tilde{x_i}||^2$$

このように、量子化前後の内積値の誤差最小化は、量子化誤差の最小化問題に置き換えられます。こういった理由で、様々な研究で再構成誤差の最小化に焦点が当てられています。このように、すでに十分適切な目的関数が設計されているようにも思えますが、著者らは加えて距離関数に"MIPS"を使う場合を見据えた以下の観点にも着目しています。

内積の高いペアの損失に大きな重みを付与: 内積を引数に取る重み関数$w$の導入
- 検索精度向上に大きく影響する上位ペアを重視
- 上記目的関数はデータポイント$x$とクエリ$q$の全ての組み合わせを考えている
量子化誤差を平行方向・直交方向の異方性加重話に分解
- 内積の特性を考慮

上記の観点を反映させ、著者らが設計した損失関数は以下のようになります。導出手順や詳細は省かせていただきますが、誤差を平行方向、直交方向に分割し、加重和を取る形です。

$$l(x_i, \tilde{x_i}, w) = h_{||}(w, ||x_i||) ||r_{||} (x_i, \tilde{x_i})||^2 + h_{\perp}(w, ||x_i||) ||r_{\perp} (x_i, \tilde{x_i})||^2$$

また、著者らは上記の重み$w$は内積を考慮して設計されているため、平行方向の量子化誤差が直交方向の量子化誤差よりも大きな重みになることも示しています（省略）。

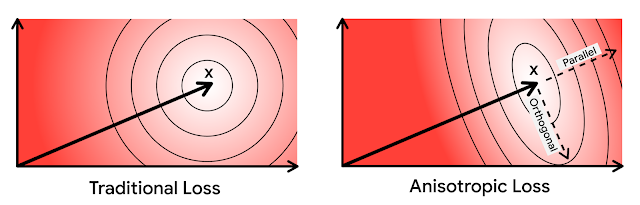
以上が著者らによって提案された異方性量子化損失関数となります。損失関数部分の提案であることから、ここまで説明してきた量子化のメカニズム自体に変更はないため、著者らの手法は広く適用することができます。

実験

次に、提案された量子化損失関数がMIPSの性能向上につながることを示すために、著者らの行ったいくつかの実験について説明します。

再構成誤差を目的関数とする手法との比較

量子化のメカニズムは揃え、従来手法と著者らの提案手法の比較を行っています。データセットはGlove1.2Mという、データ数120万、次元数100の単語埋め込みのコレクションを使用しています。

このデータセットを量子化した時のRecall 1@10（検索された上位10件のうちに真のTop1データポイントが含まれるクエリの割合）の比較を下図(a)に、量子化前後のTop1データとの内積の相対誤差を下図(b)に示しています。これらに示されているように、損失関数のパラメータ$T$が適切であれば、提案された損失関数が大幅な再現率向上を達成し、加えて上位ペアとの相対誤差も小さくなっていることがわかります。

MIPS精度と速度の比較

次に、他の量子化技術（LSQ、QUIPSの3つの派生）とのMIPS精度の比較を行います。下図(a)はデータポイントあたり100ビットと200ビットの固定ビットレートで性能を測定しています。Recall 1@Nの指標における全ての範囲のNにおいて、著者らの提案手法が優れていることがわかります。

また、ANN-Benchmarksのベンチマークプロトコルに従い、Glove1.2Mでのパフォーマンス測定を行った結果は下図(b)になります。競合する手法を大幅に上回っていることがわかります。

通常、精度と速度のトレードオフになると考えられている領域で、両面で圧倒しているのでやはり優れた手法であると言えます。

まとめ

MIPSは機械学習の応用において、CVや自然言語など分野を問わず非常に重要な技術だと思われるため、この分野の発展は注目に値すると思います。個人的には、大規模環境の想定など、実務寄りの課題も含まれた研究分野という点で面白いと感じています。また、今後はベクトル検索においても、検索対象のフィルタリング（データベースの構造化）のようなことができるようになったら嬉しいなと感じています。