AI Cures Intractable Diseases! Using Reinforcement Learning To Propose Medication Management For Parkinson's Disease!
3 main points
✔️ Many factors in Parkinson's disease change as the disease progresses, making decision-making for medication management difficult.
✔️ We propose a model to minimize motor symptoms of PD using reinforcement learning and taking individual characteristics into account.
✔️ The results of this evaluation show promise for the development of models that can enhance the management of Parkinson's disease with the introduction of RL
Computational medication regimen for Parkinson’s disease using reinforcement learning
written by Yejin Kim, Jessika Suescun, Mya C. Schiess, Xiaoqian Jiang
(Submitted on 129 Apr 2021)
Comments: nature
The images used in this article are from the paper, the introductory slides, or were created based on them.
background
Can AI develop more effective treatment plans than specialists?
In this study, we apply Reinforcement Learning (RL) to Parkinson's disease (PD), which is an intractable disease. -We propose a learning model that aims to minimize motor symptoms in
PD is a rapidly increasing type of neurodegenerative disease with an ever-increasing patient population and economic cost. While palliative treatment with dopamine replacement is the mainstay of treatment, many factors change as the disease progresses, making medication management difficult. While treatment guidelines have been proposed, interventions need to take into account individual characteristics, and a vast array of factors need to be considered in decision-making - in actual clinical practice, patients should be started on low-dose monotherapy, with dosage adjustments and adjunctive therapies added according to patient response and condition. The following is a brief overview of the results of this study. This process involves determining the appropriate combination of medications to improve quality of life, taking into account the motor symptoms of PD; these decisions require consideration of many factors and flexibility - including adaptive changes based on the patient's condition. Human decision-making is difficult. In this study, we aim to derive robust and optimal drug combinations that take into account individual characteristics - the pathophysiology of each PD - by utilizing RL.
What is Parkinson's Disease - Parkinson's Diseases: PD?
First, a brief description of Parkinson's Disease (PD), the subject of this study, is given.
Parkinson's disease (PD) is a neurodegenerative disease that has been rapidly increasing in recent years. The main symptoms are movement disorders such as tremors, slow movements, muscle stiffness, and postural retention disorder, which makes it easy to fall. Nonmotor symptoms may include constipation; frequent urination; sweating; easy fatigability; the decreased sense of smell; orthostatic hypotension; dizziness; lack of clarity -PD is projected to affect 17.5 million people worldwide by 2040, with a 74.3% increase in prevalence since 1990 and an estimated $52 billion annual economic burden in the United States. Pharmacotherapy is the predominant treatment strategy for PD - it replenishes dopamine neurons, which are depleted, to alleviate symptoms; pharmacological management, including medication, is dependent on a variety of factors, including individual factors, such as disease progression. The difficulty of decision-making is a challenge.
research purpose
In this study, we utilize reinforcement learning -Reinforcement learning: RL- to aim for an optimal treatment strategy to minimize motor symptoms of PD.
As mentioned above, in PD, it is necessary to determine a treatment policy that takes individual factors into account, which is complicated and involves a vast number of factors, making human decision-making difficult. Therefore, in this study, we aim to derive the optimal treatment policy that takes individual characteristics into account using RL. The importance of interpretability and robustness of the derivation policy across studies is also important. Therefore, in this study, we utilize decision tree regression for interpretability and ensemble learning for robustness and aim to improve clinical usefulness.
technique
In this chapter, we provide an overview of the proposed method. The proposed method uses the Parkinson's Progression Markers Initiative (PPMI) database, a longitudinal observational cohort of PD patients, to develop a Markov The MDP (Decision Process) environment was constructed and iteratively learned to derive clinically relevant disease states and optimal drug combinations. Eight drug combinations, including the dopamine agonist levodopa and other PD drugs, were used as agent options to assess motor symptoms using the Unified Parkinson Disease Rating Scale -UPDRS-III-based scores as rewards and penalties.
data-set
In this section, we give an overview of the dataset, which is utilized for the proposed method.
This study utilizes PPMI as a retrospective cohort study; PPMI is an observational study initiated in 2010, including the Hoehn and Yahr stage, UPDRS III, and other clinical assessments and medications - levodopa, dopamine agonists, other PD medications - are being collected. The analysis included 431 patients with early PD who were followed up for 55.5 months for a total of 5077 visits; patients with no UPDRS III scores or medication records were excluded. Most cases were also treated with a combination of levodopa, dopamine agonists, and other PD medications - MAO-B inhibitors, COMT inhibitors, amantadine, and anticholinergics. To measure the rate of PD progression, UPDRS The percentage change in the total score of III was calculated.
Utilization of Markov Decision Process (MDP)
In this chapter, we describe how to utilize MDP in the proposed method.
Medication management consists of three components - current medical condition, medication options, and total UPDRS III score - and the clinician determines the combination of medications based on the current medical condition - this combination affects motor symptoms and can be interpreted as a change in the current medical condition. The purpose of this model is to select the optimal pharmacotherapy based on these combinations and to minimize the total score in the UPDRS III.
In this study, we model the treatment using a Markov Decision Process (MDP), in which an agent chooses an action to maximize the estimated reward -The agent explores a huge number of actions and selects the optimal action to maximize the cumulative reward. The configuration of each element is as follows:
(1) State 𝑠: disease state action at the current visit
(2) Behavior 𝑎: 8 combinations of therapeutic levodopa and other PD medications
(3) Reward/penalty 𝑟(𝑠,𝑎,𝑠'): patient's response to the medication: specifically, the cumulative UPDRS III score and the behavior The number of drugs at 𝑎 multiplied by a weighted constant 𝑐
In the formulation, we utilized decision tree regression and defined disease states using multiple factors - PD subtype, Hoehn and Yahr stage, age at presentation, UPDRS III total score and rate of change, etc. Transition probabilities between these states were calculated by counting each transition observed in the PPMI trajectory and dividing by the total number of transitions. TD learning was used to construct the RL model.
Ensembles on treatment plans
In this chapter, we describe ensemble learning that improves the robustness - robustness - of the treatment strategy.
We utilize the ensemble approach proposed by RL to increase the robustness - consistency across studies - of the treatment strategy. The procedure is as follows: divide the dataset into 80% training and 20% testing; derive the treatment strategy from the training by RL and the clinician, and Evaluate these estimated rewards - or penalties - on the test set; resample the training and test randomly 500 times and calculate the distribution of estimated rewards (see below). We then bootstrap 500 times and select the optimal treatment strategy by majority vote.
result
In this section, we describe the evaluation results for the treatment strategies derived by the RL model.
First, we used a multivariate regression model to determine whether the clinical endpoints - disease state - and drug - action - were related to the UPDRS III score - penalty - in the statistical significance to the predictions (see table below).
Statistically significant variables and a decision tree regression model were then used to regress the UPDRS III total score on the UPDRS III total score to derive the associated condition. The disease states were motor stiffness, tremor-dominant, and mixed, with corresponding scores of 21, 4, and 3, respectively. In the present study, disease states were defined by the total UPDRS III score, change - the difference between the previous and the present score - and age. Other variables - such as cognitive score and Hoehn and Yahr stage - while statistically significant, were not used to define disease state because of their low significance in decision tree regression.
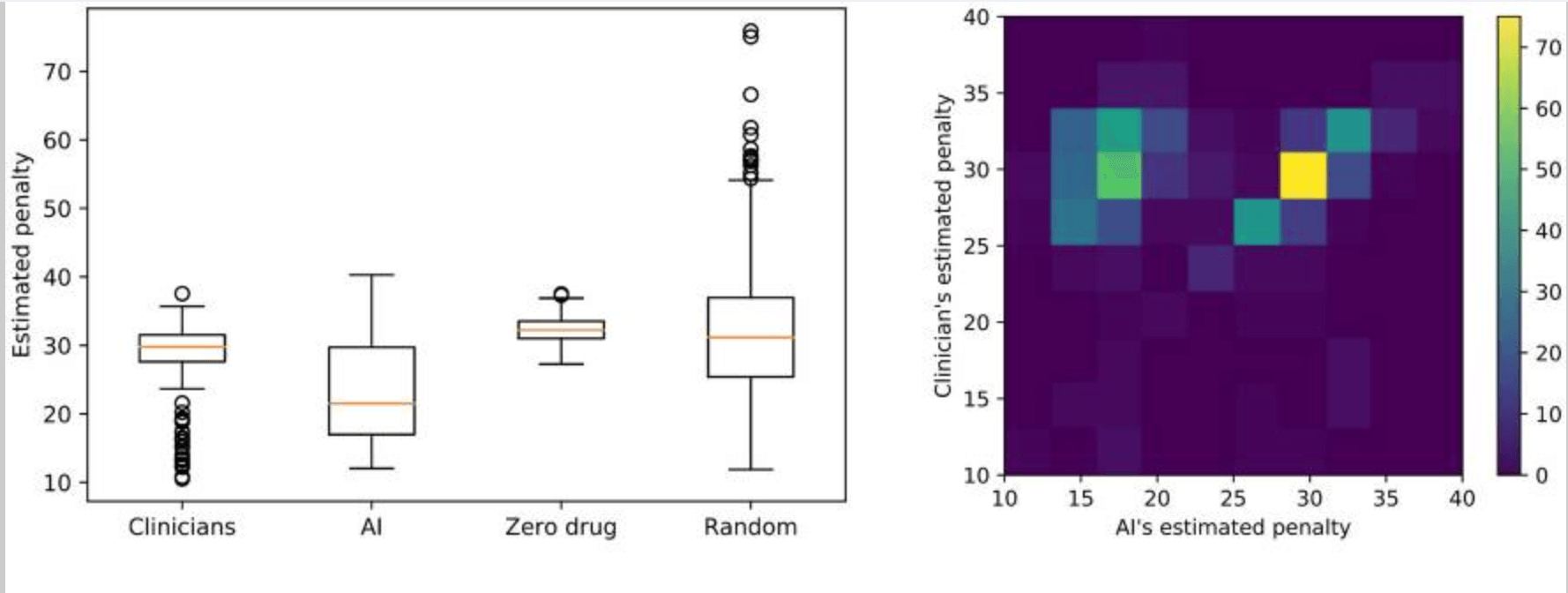
The RL model-derived the optimal behavior that minimized the median penalty - the cumulative UPDRS score - from the disease state (see figure below).
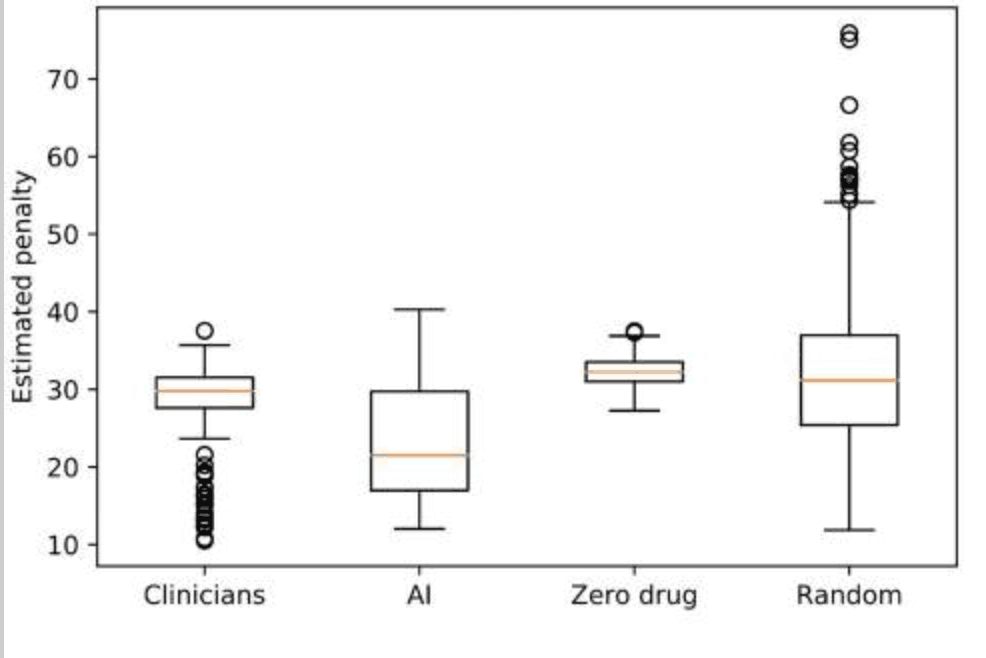
The median penalty values were 29.8 for clinicians and 21.5 for AI, with the range and variance as follows: clinicians: min = 10.5, max = 37.6, var. = 16.1; RL: min = 12.0, max = 40.3, var. = 47.4. These results suggest that the proposed model for medication policy resulted in instability but lower penalties - fewer motor symptoms; whereas the clinician's medication policy suggested greater stability but higher penalties - more motor symptoms The results of the study were as follows. When comparing RL and clinician penalty distributions using the same training/test set, RL penalty scores were smaller or similar to clinicians. In addition, the medication policies derived from the clinician and the proposed model achieved significantly lower penalties than the zero or random policies - t-value = -16.7, p-value = 1e-55: clinician vs zero drugs, t-value = -6.2, p-value = 1e-10: clinician vs random drug The results of the study were as follows.
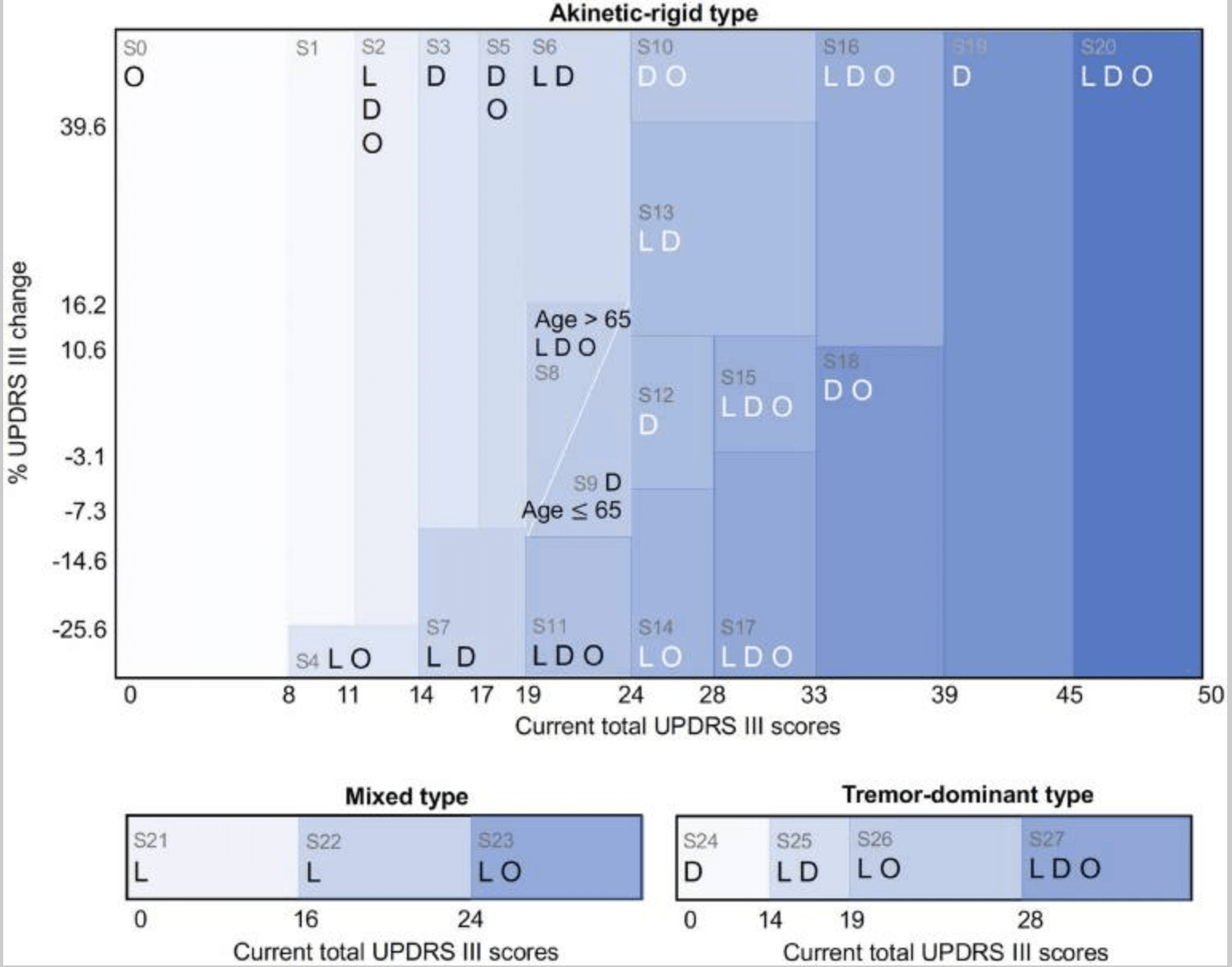
In addition, while the clinician's treatment strategy and the RL's recommended actions (see below) were largely the same, the RL model proposed specific pathological changes together - in 16 of the 28 conditions, the RL proposed the same actions as the clinician and in 12, different actions: for example, in the In condition 1, an early stage of motor stiff PD with a cumulative UPDRS III score of 9-11, the clinician prescribes a dopamine agonist, but the RL model suggests withholding the drug. In condition 9 - a mild form of rigor mortis PD - with a total UPDRS III score of 20 to 24 and age <65 years, clinicians prescribe levodopa and dopamine agonists, whereas the AI model suggests taking dopamine agonists only.
consideration
This study utilized RL to develop a robust model for deriving optimal drug combinations for motor symptoms of PD disease. We used an observational longitudinal cohort of PD patients - PPMI - to propose optimal drug combinations for each condition by iterating Markov decision processes. As a result of the derived combinations, the proposed model outputs medication regimens with performance comparable to that of clinicians and achieves lower levels of motor symptom severity scores than clinicians; whereas clinicians' treatment strategies are more consistent than the proposed model. The proposed model was based on the clinician's treatment plan but proposed several changes, which led to differences in reduced severity.
One of the strengths of the proposed model is that it can be used in an outpatient setting: it is easy to interpret by utilizing the notation for severity. In addition, by using the PD subtype as the initial node, we have defined the disease states based on the clinician's experience; therefore, the disease states defined in this study are likely to be easy to interpret clinically.
On the other hand, challenges are assumed to include: poor consistency of the proposed model; inconsistent UPDRS scores. While the proposed model shows higher performance - lower UPDRS scores - it results in greater variability for the estimated penalty - less consistent across different trials than clinicians' medication guidelines. These may be due to trial-and-error exploration in the behavioral space - drug combinations in each condition. Solutions include improving accuracy in ensemble learning - random forests, gradient boosting - and complementing each other by combining RL and physician treatment strategies. In some cases, the UPDRS rate of change showed negative values that were inconsistent with normal disease progression; possible reasons include the small cohort size in the dataset analyzed and inconsistency in the UPDRS III score. As a solution, we are considering introducing a method other than this score to assess motor function.
Categories related to this article
