![[Materials Informatics] Matlantis™, A General-purpose Atomic-level Simulator](https://aisholar.s3.ap-northeast-1.amazonaws.com/media/January2022/matlanti.png)
[Materials Informatics] Matlantis™, A General-purpose Atomic-level Simulator
3 main points
✔️ Joint development by Preferred Networks and ENEOS
✔️ Potentially learns complex theories of chemistry and solid-state physics that explain material phenomena
✔️ Achieves superior versatility without the need for learning for each target task
PFP: Universal Neural Network Potential for Material Discovery
written by So Takamoto, Chikashi Shinagawa, Daisuke Motoki, Kosuke Nakago, Wenwen Li, Iori Kurata, Taku Watanabe, Yoshihiro Yayama, Hiroki Iriguchi, Yusuke Asano, Tasuku Onodera, Takafumi Ishii, Takao Kudo, Hideki Ono, Ryohto Sawada, Ryuichiro Ishitani, Marc Ong, Taiki Yamaguchi, Toshiki Kataoka, Akihide Hayashi, Takeshi Ibuka
(Submitted on 28 Jun 2021)
Comments: Published on arxiv.
Subjects: Materials Science (cond-mat.mtrl-sci); Computational Physics (physics.comp-ph)
code:

The images used in this article are from the paper, the introductory slides, or were created based on them.
Matlantis™, a general-purpose atomic-level simulator
Matlantis™" was born by the joint development of Preferred Networks and ENEOS. Matlantis™.
This service can be used to predict the performance of materials, simulate and explore materials using machine learning. This service is attracting a lot of attention in the field of materials informatics because of its high versatility.
This time I would like to introduce "PFP" which is used in "Matlantis™". This paper is contributed by Preferred Networks and ENEOS.
Material Search and Neural Network Potentials (NNPs)
There are a variety of elements in this world, and the number of substances consisting of their combinations is astronomical. Computer simulations based on quantum chemical theory, such as DFT calculations, are effective for handling these substances.
However, it is difficult to utilize DFT calculations for comprehensive material searches. This is because simulations such as DFT calculations at present are computationally expensive. In addition, the more complex the structure is, the longer the calculation time becomes.
Therefore, substance search methods using machine learning have been attracting attention. In particular, Neural Network Potentials (NNPs), which combine neural networks with huge data sets, have attracted much attention.
However, there is an issue. That is the lack of versatility. In many cases, models created with data sets for specific substance groups cannot be used to predict other substance groups. It is also extremely difficult to accurately predict the performance of substances with unknown structures. Thus, NNP also has significant challenges. However, inspired by the results that NNP can predict accurately even with a small number of data sets and parameters, we aimed to build a general-purpose model using NNP in this study.
In particular, the dataset prepared in this study has the following characteristics.
- Even for unstable material structures, we actively collect data that we believe is important to improve the robustness and versatility of our models.
- Some of them have irregularly replaced atoms constituting known crystal structures and molecules, some have structures in which various elements exist in disorder, and some have changed their surrounding environments such as their temperature and density.
Finally, in this study, we developed a model called Pre-Ferred Potential (PFP), which is a general-purpose NNP. The PFP can handle various combinations of 45 elements in the periodic table. The PFP model is mainly used to predict the potential energy surface, which is the basis for the prediction of physical properties, from the atomic structure.
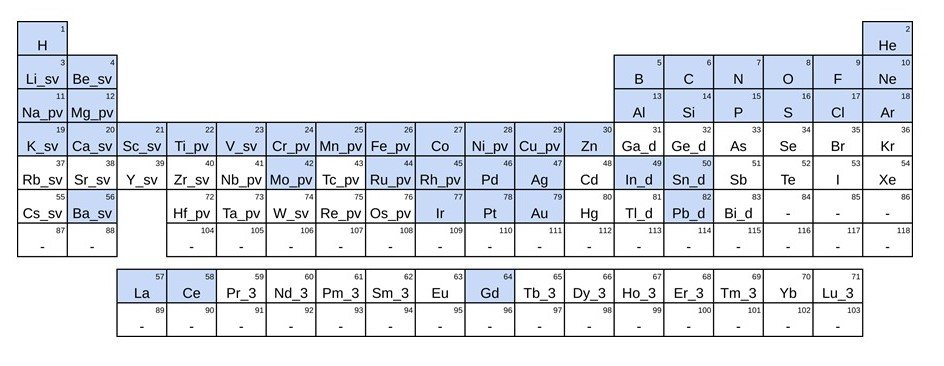
Figure 1 Elements that can be handled by PFP (blue: elements that can be handled)
model building
The NNs of the neural network potentials (NNPs) are multiplied by several properties for the description of the atomic structure.
That is rotational invariance (SO(N)), translational invariance (SE(N), including rotational invariance), and mirror-image inversion invariance (E(N), including rotational invariance and translational invariance) of material structures. To improve the performance of describing atomic structures, it is also necessary to design them in such a way that higher-order features related to the positional coordinates of atoms, etc., are not lost.
For example, Atomic Environment Vectors (AEVs) and node-based Machine-Learning Potentials (MLPs) represent the positions of atoms in terms of bond distances and angles.
They can adequately represent location relations while maintaining the invariance described above. However, they have the disadvantage that they do not have a message-passing mechanism like Graph Neural Networks (GNNs), which makes it difficult to convey location information over a distance. Therefore, as shown in Table 1, various existing methods are built to handle higher-order features in GNN structures.
Table 1 Existing models consisting of MLP and GNN
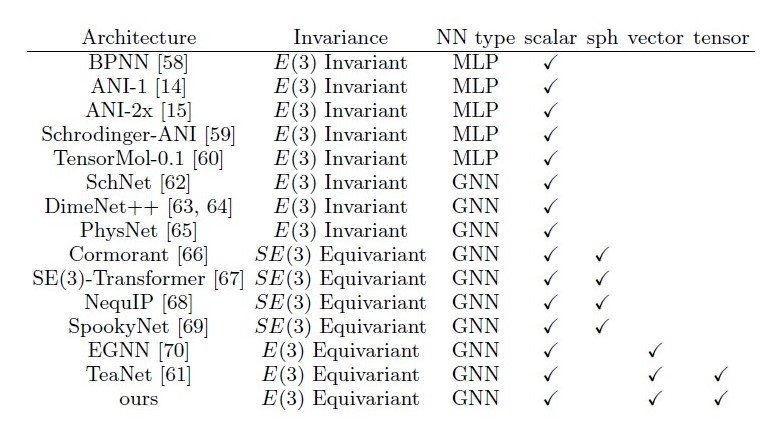
Among these, TeaNet has E(3) invariance and can handle higher-order features such as second-order tensor quantities.
Therefore, the authors have adopted a GNN structure with TeaNet-style tensor-based convolutional layers as the core of the model addressed in this study. Although the NNPs structure in this study is a GNN structure, it is a local interaction model and is set up so that infinitely distant atoms do not interact with each other. This setting leads to reduced computational cost and improved versatility.
And in DFT and molecular dynamics calculations, the stability of the calculation contributes to the smoothness of the resulting energy surface. Occasionally, higher-order derivative calculations may be required.
Therefore, the structure of our model is designed so that the energy is differentiable to higher orders concerning the atomic position.
data set
Public datasets such as Materials Project (MP) contain data of "optimized structures" of materials obtained by DFT calculations and so on. However, the optimized structure alone is not sufficient to realize the generic potential for material discovery.
This is because chemical reactions, diffusion phenomena, and crystal phase changes often proceed in states that are far from the optimized structure. Therefore, in this study, in addition to the optimized structure, oscillatory and disordered structures were collected as data to realize a generic potential. As the data set continues to expand, this mechanism for learning data under various conditions is expected to become more effective.
Table 2 shows the list of public datasets and the types of data in the dataset constructed in this study (bottom).
Table 2 Various public data sets and their contents
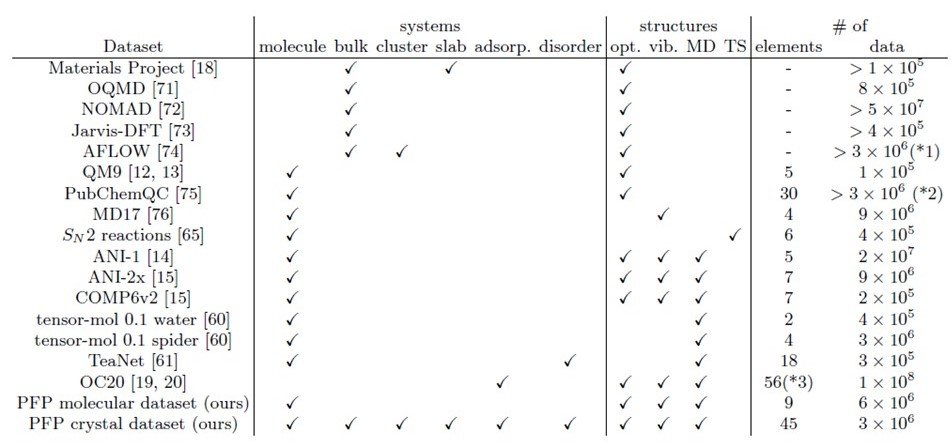
As a system, the
- molecule: molecular structure (mainly small organic molecules)
- bulk: Crystal structure (without considering the surface)
- cluster: a small aggregate of atoms
- slab: surface structure
- adsorp. : adsorption structure of molecules on a surface
- disorder: disordered structure, amorphous structure (not crystalline)
and the public dataset holds only a part of each of them, while the dataset in this study is exhaustive.
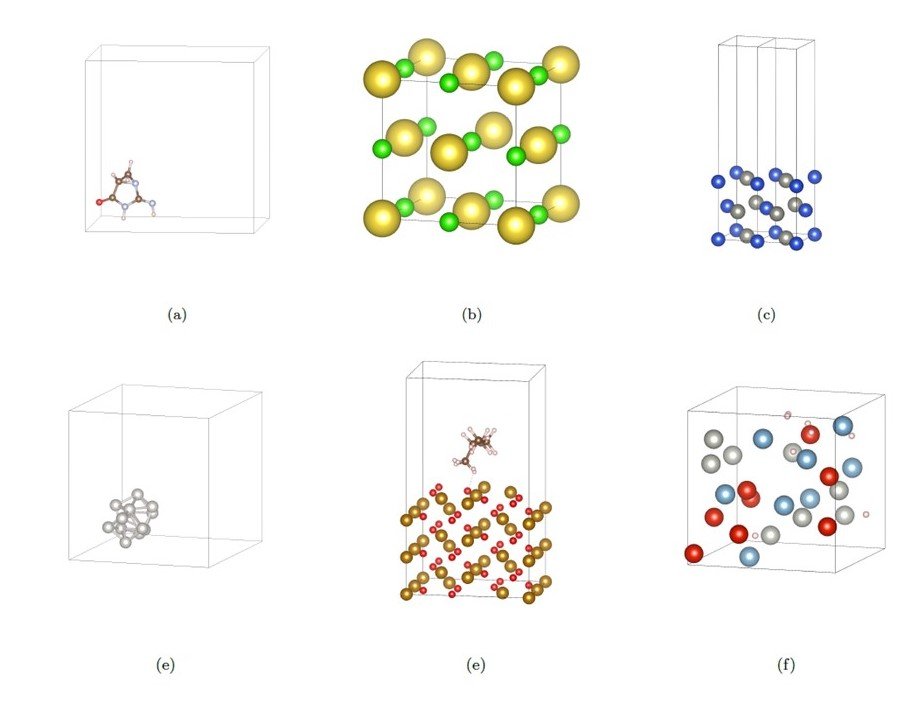
Figure 2 Images of each structure represented in a cell used for DFT calculations. (a) molecular structure, (b) crystal structure, (c) surface structure, (d) cluster structure, (e) adsorption of molecules on the surface, (f) disordered structure.
And as for the structure
- opt. : Optimized structure (the most stable structure with the lowest energy)
- vib. : vibrating structure
- MD: Structure with change obtained by molecular dynamics (MD) simulation
etc., and our dataset has data for these various structures. The data set also covers 45 kinds of elements.
The calculation speed of PFP
We evaluated the calculation speed of DFT calculation and PFP, which are typical simulation methods. Surprisingly, PFP takes only 0.3 seconds to calculate 3000 platinum (Pt) atoms.
On the other hand, it takes "about two months" to obtain the same information by DFT calculation. By simple comparison, it can be said that the calculation speed of PFP is 20 million times faster than that of the DFT calculation. In other words, if values are calculated using a trained machine learning model (PFP) instead of a DFT calculation, the calculation cost can be significantly reduced.
However, to train the model, we have to use data sets obtained mainly by DFT calculations. This is where public databases should be used as effectively as possible.
Application examples of PFP and its performance
-diffusion behavior of lithium ions
We will now introduce two prediction tasks for the system using PFP.
The first example is the prediction of the diffusion behavior of lithium ions in materials used in lithium-ion batteries.
One of the important properties of lithium-ion batteries is their charge and discharge rate. The higher the diffusion rate of lithium ions in the material used, the lower the activation energy (like an energy barrier for the reaction, the lower the energy barrier the faster the reaction) and the higher the charge/discharge rate. Normally, calculation of activation energy by DFT calculation requires the calculation of the intermediate, or transition, state between the pre-reaction and post-reaction states.
And to obtain the structure and energy of the transition state (saddle point) precisely, we need a smoother and more reproducible potential. Naturally, the transition state is far from the optimized structure of matter (the most stable structure) or the harmonic vibrational state.
LiFeSO4F with a tavorite structure is one of the cathode materials for lithium-ion batteries and exhibits a high voltage of 3.6 V. According to the results of conventional DFT calculations, this material shows a one-dimensional lithium-ion diffusion behavior. In other words, only the lithium-ion diffusion in the one-dimensional direction results in low activation energy.
In this study, the activation energy of lithium-ion diffusion in LiFeSO4F was obtained by the CI-NEB method (the detailed explanation is omitted because it is a term related to DFT calculation) using PFP.
The obtained diffusion paths of lithium ions in LiFeSO4F are shown in Figure 3. The activation energies obtained are shown in Table 3.
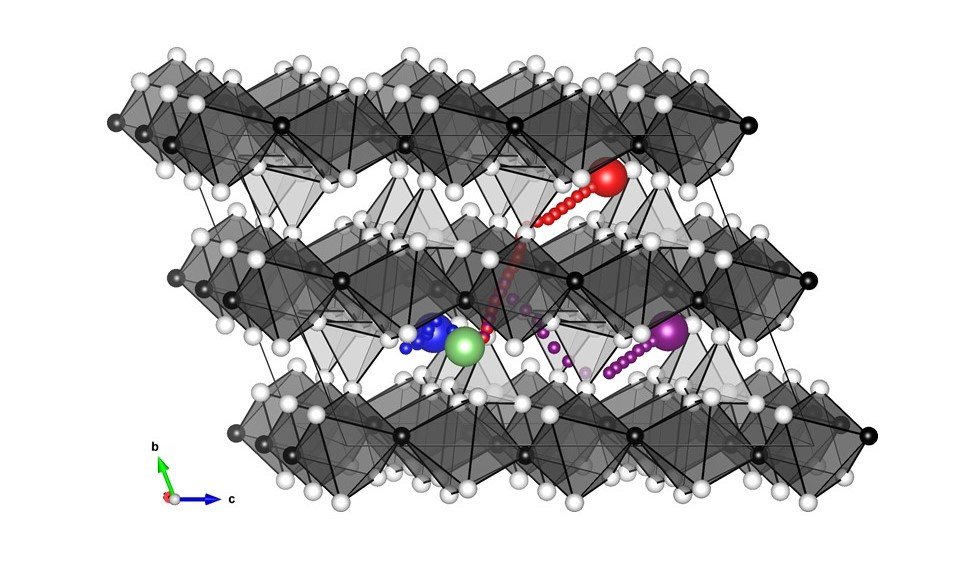
Figure 3 Diffusion path of lithium in LiFeSO4F obtained by PFP, green circle is the initial position, the red circle is the position after diffusion, purple and blue circles are from the green circle. The purple and blue circles show the diffusion paths in different directions from the green circle. (White circle: O, black circle: F, dark gray circle: Fe, light gray circle: S)
Table 3 Activation energies obtained by PFP for the Activation energy of lithium diffusion by LiFeSO4F, calculated in three directions.

As a result, the PFP reproduces well the diffusion behavior only in the one-dimensional direction obtained by the conventional DFT calculation.
Moreover, surprisingly, PFP accurately calculated the energies of the transition states that are far from the optimized structure, even though no prior information on the transition states or reaction mechanism was given. Incidentally, PFP took only five minutes to perform this calculation on a single GPU.
-Exploring the catalytic materials for the Fischer Tropsch reaction
The following example is a catalytic materials search for a reaction called the Fischer Tropsch reaction.
This reaction is an industrial catalytic reaction that synthesizes various hydrocarbons ( CxHy ), which can also be used as fuels, from hydrogen ( H2 ) and carbon monoxide (CO) gases. It consists of complex elementary processes.
Nanoparticles of cobalt (Co) are loaded on the surface of a material called a support, which acts as a catalyst to promote the reaction. In this example, we are particularly interested in the methanation reaction and the carbon monoxide (CO) dissociation reaction, which are important elementary processes in this reaction.
Figure 4 shows the correlation between the values of activation energies in the methanation reaction obtained by PFP and conventional DFT calculations. The existence of several different activation energies is considered to be because several tests were performed with different elementary processes and reaction conditions. The results show that the correlation coefficient is 0.98 and the MAE is 0.097 eV, which means that the prediction was successful with high accuracy.
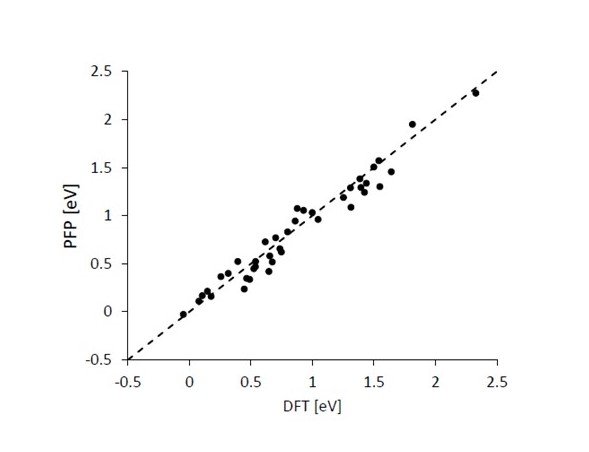
Figure 4. Correlation of activation energy values for methanation reactions obtained by PFP and conventional DFT calculations.
Then, we searched for additive elements that promote the CO dissociation process on the cobalt surface.
The CO dissociation process is an important elementary process in the Fischer-Tropsch reaction, and it is important to reduce the activation energy of this process to create effective catalytic materials.
However, it is not cost-effective to perform an exhaustive search for added elements only by DFT calculations, so we tried to improve the efficiency by PFP. The screening was performed by replacing some of the cobalt atoms in the cobalt catalyst with other atoms. The results of the activation energy calculation are shown in Figure 5.
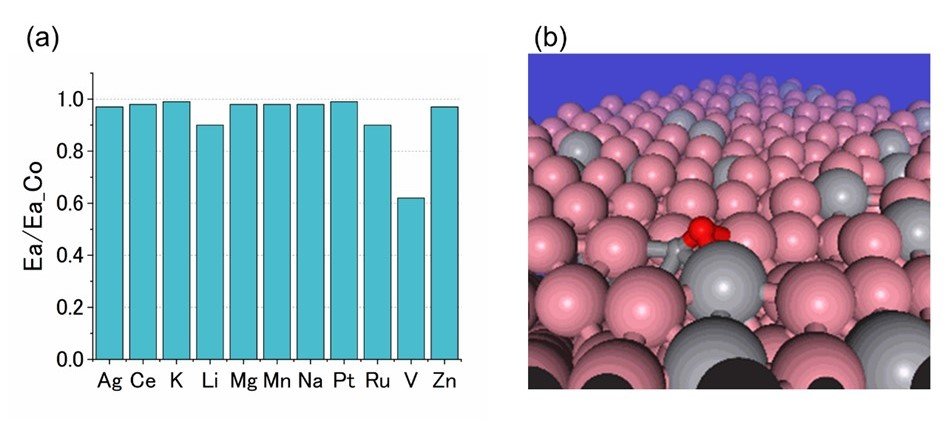
Figure 5. (a) Comparison of activation energies of CO dissociation reactions on Co catalysts substituted with various elements (normalized), (b) Visualization of CO dissociation reactions on Co catalyst surfaces containing V (pink: Co, gray: V, red: O, small gray: C).
Eleven elements were tested and it was found that vanadium (V) reduced the activation energy by nearly 40%.
Although vanadium was known to be effective in previous studies, PFP did not provide this prior information. In other words, it can be said that we succeeded in efficient and effective screening by PFP. In addition to the above two examples, other examples showing the effectiveness of PFP have been introduced. If you would like to know more, please refer to the original paper.
Future Prospects for Developers
The PFP introduced here is Version 0, and a project to develop the PFP is still in progress.
Data set side: Expansion of the applicable range of element types, parameters, and structures that can be handled
Model structure side: Attempt to introduce charge transfer and long-range interaction between atoms into the model
Looking at the current official Matlantis website, the number of applicable elements seems to be even higher. (Currently, 55 elements are supported) Official site
summary
In this article, we introduced the substance search by PFP, which has versatility potential.
This PFP has powerful expressive and descriptive power by learning an unprecedentedly diverse data set of materials with a unique GNN structure.
As a result, we obtained a model (potential) with excellent versatility, which does not require the training of a model for each task. Conventionally, the extrapolation task, which is important for the search for unknown substances, has been difficult and there have been few effective models. However, this PFP has a great potential to be applied to such extrapolation tasks. We look forward to future work.
And in the future, by learning even more diverse data sets with the improved PFP and improving its expressive power, it may become like an expert machine for materials. It's exciting.
Categories related to this article



.jpg)




