SoTA For Similar Vector Search! Introducing ScaNN, A Method Used In GCP: Vertex Matching Engine!
3 main points
✔️ The original paper on GCP's new product, Vertex Matching Engine
✔️ Proposed a new quantization loss function that takes into account MIPS scores
✔️ Record SoTA performance on ANNBenchmarks
Accelerating Large-Scale Inference with Anisotropic Vector Quantization
written by Ruiqi Guo, Philip Sun, Erik Lindgren, Quan Geng, David Simcha, Felix Chern, Sanjiv Kumar
(Submitted on 27 Aug 2019 (v1), last revised 4 Dec 2020 (this version, v5))
Comments: Published as a conference paper at ICML 2020.
Subjects: Machine Learning (cs.LG); Machine Learning (stat.ML)
code:
First of all
ScaNN was announced by Google to speed up similarity vector search on the famous benchmarking site " ann-benchmarks.com ", and it is the method that has recorded the most advanced performance. The other day. GCP. Vertex Matching Engine which realizes similarity vector search with great performance was released (preview version) on GCP recently. Since this is a high-profile product, I'd like to take this opportunity to introduce the original paper.
Similarity Vector Search can be applied to various services and is often used in combination with Machine Learning. However, if you look at the documentation of Vertex Matching Engine, you will see that it can withstand a huge data scale and QPS, so I am personally looking forward to Vertex Matching Engine.
Similar vector search
Similarity vector search (also called nearest neighbor search) has become a popular technique for solving large-scale classification and search tasks. In particular, it has become a very general-purpose technique because machine learning models map data into an embedding space, allowing us to answer abstract queries that were previously difficult to answer (flow as in the gif below). For example, it can be applied to recommending similar products, similar images, and similar documents.
A common method to achieve nearest neighbor search is Maximum inner product search (MIPS) using the inner product distance. The problem of MIPS can be formally defined as follows.
Consider a database $X={x_i}, i=1,2,...,n$ with $n$ data points. Each data point $x_i \in R^d$ is in a $d$-dimensional vector space. Here, given a query $q \in R^d$, the task is to identify the data point $x \in X$ with the largest inner product with $q$, i.e.
$$x_i^* := arg max \left< q, x_i \right>$$
Here, since databases are usually large, it is often impractical to exhaustively compute the inner product of a query $q$ and all data points ($\mathcal{O}(Nd)$ with $N$ number of data and $d$ number of vector dimensions). Therefore, even if the data points are not strictly nearest neighbor, approximate nearest neighbor search that speeds up the search is generally used, and techniques based on hashing, graph search, quantization, etc. have been proposed in various studies.
MIPS Efficiency
There are two main challenges to developing an efficient MIPS system.
- Reducing the number of data points to compare against a query
- Tree structures, graphs, spatial partitioning using hash functions (which preserve similarity), and other methods
- Compare only with data in the subspace relevant to the given query
- Compression of data points
- Vector quantization methods are the state-of-the-art
- Compression provides various benefits, such as reduced computation for inner products, improved resource efficiency through reduced memory usage, and reduced storage.
Various methods have been proposed to deal with these issues, as described above. The contribution of the authors is in the quantization part, where they proposed a quantization loss function that considers not only the speed aspect but also the MIPS accuracy, which is new.
In the following, we first describe the quantization, but if you already know it, you can skip to the part of the authors' proposed method.
Vector quantization
Taking direct product quantization, which is a general method of vector quantization, as an example, the basic idea and procedure in quantization can be briefly explained as follows.
- (Prep) Building the codebook
- Divide the vector into $M$ parts and consider them as $M$ $d/M$-dimensional vectors
- Compute k-means of data points in the database
- (Advance preparation) Quantize all data points in the database using the codebook.
- Compressed from a $d$-dimensional vector of type float to a $M$-dimensional vector of type uint
- $32 \times d$ bit $\rightarrow$ $8 \times M$ bit
- (At query time) Quantize query data and search from PQ code of database
Given a query vector, the image of the quantization is shown in the figure below. In this step, we also record the distance table between the query and each codeword.
After quantization, the distance table calculated in all steps is used to linearly search for the closest distance from the group of PQ codes in the database.
This allows the search problem, which originally cost $\mathcal{O}(Nd)$ and was impractical on a large scale, to be realized with much less computation, $\mathcal{O}(dK + MN)$.
Building a codebook
In this section, we describe the preliminary preparation, the construction of the codebook. The optimization problem in codeword selection can be formulated as follows.
$$min_{c_1, c_2, \cdots, c_k \in \mathbb{R}^d} \sum_{x_i} min_{\tilde{x_i} \in \{c_1, c_2, \cdots, c_k\}} ||x_i - \tilde{x_i}||^2$$
This is actually the same form as the optimization problem solved in k-means, and It can be solved by the same algorithm as k-means. Below are the steps to create a The procedure for creating a codebook is shown below.
- (Initialization step) Initialize the codewords $c_1, c_2, \cdots, c_k$ as random data points sampled from $x_1, \cdots, x_n$.
- (Partition assignment step) For each data point $x_i$, find the codeword $\tilde{x_i}$ with the closest distance
$\tilde{x_i} = arg min_{\tilde{x_i} \in c_1, cdots, c_k} l(x_i, \tilde{x_i})$ - (Update codebook step) When $X_j$ is set to all data points $x_i$ such that $\hat{x_i} = c_j$, update each codeword $c_j$ according to the following formula.
$c_j \leftarrow arg min_{c \in \mathbb{R}^d} \sum_{x_i \in X_j} l(x_i, c)$ - Repeat step 2 and step 3 until convergence is achieved or the maximum number of iterations is reached
In each iteration, an update step needs to be performed for each codeword. For the sake of simplicity, the explanation here does not assume vector splitting, but the same procedure can be used for direct product quantization.
Also, the distance function $l$ used in common quantization techniques focuses on minimizing the reconstruction error when quantizing a data point $x$ to $\tilde{x}$.
Space division
In vector quantization, the same effect as spatial decomposition can be obtained by devising the encoding method. For example, we can consider the following Voronoi space partitioning as well as k-means.
Once the corresponding codeword region of the query vector is determined, the idea is to quantize and record the residual $r_q=q-c_i$ of the distance to that codeword. This also improves efficiency, since the query only needs to compare data points in the same space, rather than the entire database.
Depending on the scale, this kind of mechanism is becoming mainstream when it comes to vector quantization.
Proposed method: ScaNN
We now turn to the description of the proposed method. The authors record the state-of-the-art performance of ANN-Benchmarks by proposing a new objective function, the anisotropic quantization loss function, which takes into account the improvement of the MIPS accuracy (retrieval accuracy), which is the ultimate goal.
We mentioned that existing vector quantization learns to minimize the reconstruction error during quantization as its objective function. This seems like an intermediate goal in the context of MIPS, but it is not really the case that this itself is designed to ignore MIPS accuracy.
$$\mathbb{E}_q \sum_{i=1}^n (\left< q, x_i \right> - \left< q, \tilde{x_i} \right> )^2 = \mathbb{E}_q \sum_{i=1}^n \left< q, x_i - \ tilde{x_i} \right>^2$$
$$\sum_{i=1}^n \mathbb{E}_q \left< q, x_i - \tilde{x_i} \right>^2 = \sum_{i=1}^n \mathbb{E}_q (x_i - \tilde{x_i})^Tqq^T(x_i - \tilde{x_i}) = c\sum_{i=1}^n||x_i - \tilde{x_i}||^2$$
Thus, the error minimization of the inner product values before and after quantization can be replaced by the problem of minimizing the quantization error. For these reasons, various studies have focused on the minimization of the reconstruction error. Thus, although it may seem that a suitable objective function has already been designed In addition, the authors focus on the following aspects for the case where "MIPS" is used as the distance function.
- Giving greater weight to losses of pairs with the higher inner product: Introducing a weight function $w$ that takes the inner product as an argument
- Emphasis on top-ranking pairs that have a significant impact on improving search accuracy
- The above objective function considers all combinations of data points $x$ and queries $q$.
- Decomposition of quantization error into anisotropic weighted stories in parallel and orthogonal directions
- Consider the properties of the inner product
Reflecting the above point of view, the loss function designed by the authors is as follows. The derivation procedure and details are omitted, but the error is divided into parallel and orthogonal directions, and the weighted sum is taken.
$$l(x_i, \tilde{x_i}, w) = h_{||}(w, ||x_i||) ||r_{||} (x_i, \tilde{x_i})||^2 + h_{\perp}(w, ||x_i||) ||r_{\perp} (x_i, \tilde{x_i})||^2$$
The authors also show that the above weights $w$ are designed to take into account the inner product so that the quantization error in the parallel direction is a larger weight than the quantization error in the orthogonal direction (omitted).
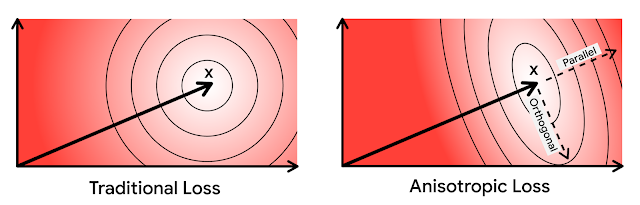
The above is the anisotropic quantization loss function proposed by the authors. Since this is a proposal of the loss function part, there is no change in the quantization mechanism itself, which has been explained so far, so the authors' method can be widely applied.
Experiment
Next, we describe several experiments conducted by the authors to show that the proposed quantization loss function can improve the performance of MIPS.
Comparison with the method using the reconstruction error as the objective function
The quantization mechanisms are aligned and a comparison is made between the conventional method and the authors' proposed method. The dataset is Glove1.2M, which is a collection of 1.2 million data and 100-word embeddings of dimensionality.
The comparison of Recall 1@10 (the fraction of queries that contain true Top1 data points among the top 10 retrieved queries) when this dataset is quantized is shown in Figure (a) below, and the relative error of the inner product with the Top1 data before and after quantization is shown in Figure (b) below. As shown in these figures, if the parameter $T$ of the loss function is appropriate, we can see that the proposed loss function achieves a significant improvement in the recall rate, and in addition, the relative error with the top pair is also smaller.
MIPS accuracy vs. speed
Next, we compare the MIPS accuracy with other quantization techniques (three derivatives of LSQ and QUIPS). In the figure below (a) we measure the performance at fixed bit rates of 100 and 200 bits per data point, and we can see that for all ranges of N in the Recall 1@N metric, the authors' proposed method outperforms.
We also follow the ANN-Benchmarks benchmarking protocol to measure performance on Glove1.2M, as shown in figure (b) below. We can see that it significantly outperforms the competing methods.
It is still an excellent method because it dominates on both sides in an area that is usually considered to be a trade-off between accuracy and speed.
Summary
Since MIPS seems to be a very important technology in the application of machine learning, regardless of the field such as CV or natural language, I think that the development of this field deserves attention. Personally, I find it interesting in that it is a research field that includes practical issues such as the assumption of a large-scale environment. In addition, I would be very happy if we can do something like filtering of search targets (structuring of database) in vector search in the future. I am looking forward to the future.
Categories related to this article




