BERTは計算が苦手?単語分散表現はどこまで数値を上手く扱えるのか
3つの要点
✔️その1 ニューラルネットワークが自然言語に含まれる数値表現を上手く処理できていると発見した
✔️その2 ELMoなどの主要な学習済み単語分散表現が計算知識を獲得していることを確認した
✔️その3 計算知識が必要な問題には文字レベルの情報を用いた単語分散表現の獲得が有効であると示した
ニューラルネットワークを用いた現在の自然言語処理において、文書中に含まれる数字の足し算や比較といった計算を必要とするような問題を解くことは難しいと言われています。こうした数値の大小や四則演算といった計算のために必要な知識はnumeracy(数値や計算に関する基礎知識)と呼ばれ、本記事では「計算知識」と呼ぶことにします。弊メディアでも以前、ニューラルネットワークの計算知識に関する話題に触れており、計算知識を要求する問題を多く含むようなQAタスクのデータセット「DROP」を作成することで、ニューラルネットワークが問題を解けなくなってしまうと紹介しました。
関連:AIには解けない「もっと難しい」QAデータセットが登場
一方で今回紹介する論文の著者らの調査によると、このDROPデータセットのうち「数値どうしの比較」や「最大の数値を抜き出す」といった計算知識を必要とする問題において、ニューラルネットワークの正答率が高いことがわかりました。すなわち、ニューラルネットワークにはすでにある程度の計算知識が獲得されているということが示唆されたのです。著者らは、自然言語処理で広く使われている単語分散表現を学習した時点ですでに計算知識が獲得されていると考え、いくつかの実験を行いました。
さらに、様々なタスクで有効であるとされている単語分散表現BERTは、計算知識の観点で評価すると性能が低いことも示されています。例えば、「71」や「seventy-one」という単語に対応する分散表現から71.0という実数値を推定するタスクを-500~500の範囲で学習したときの予測結果が下図に示されています。図よりBERTは他の単語分散表現に比べて推定の精度が粗いことが確認できます。
このように、単語分散表現を計算するモデルによって計算知識の獲得度合いに差があることが分かってきました。本記事では、ニューラルネットワークと計算知識について、主要な実験を引用しながらご紹介します。
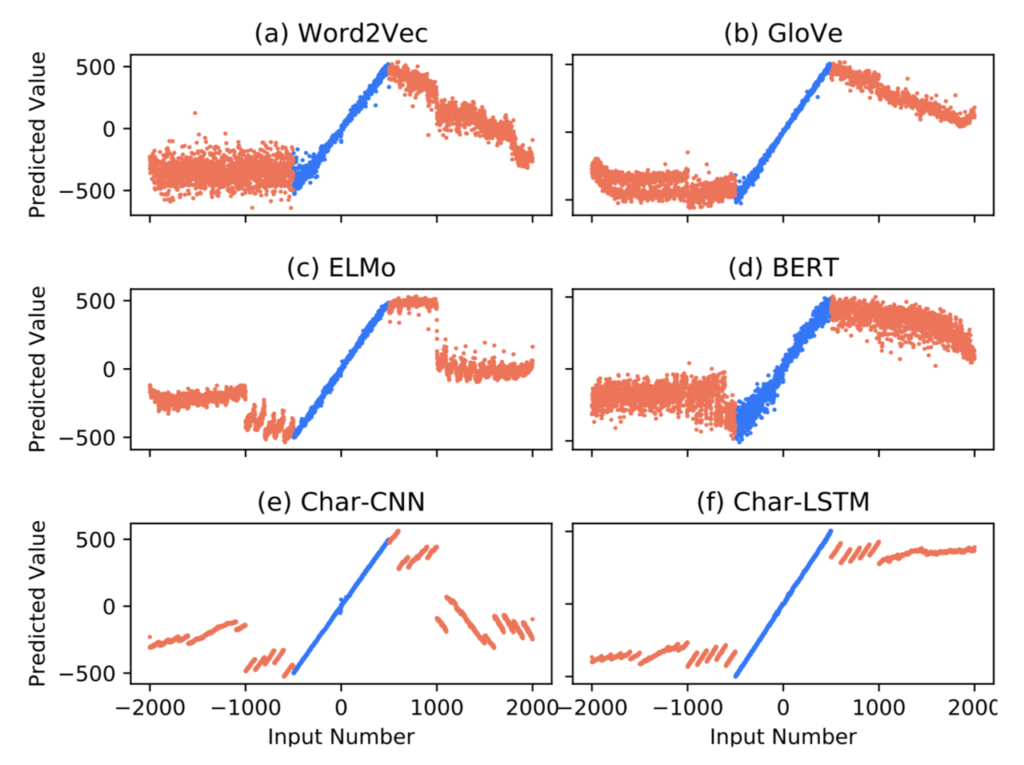
横軸が「seventy」「71」といった入力単語に対応する数値、縦軸が単語から予測された実数値を示す。単語から対応する実数値を予測する単純なタスクにも関わらず、単語分散表現による計算知識の差が確認できる。
実はニューラルネットワークは数値を扱えている?
以前弊メディアで紹介したDROPというデータセットでは、「ニューラルネットワークを用いたモデルでは計算知識や数値の処理を必要とするQAタスクを解くことができない」という仮定に基づき、計算知識を要求する問題を多く含むQAデータセットを作成しました。このDROPというデータセットを作った著者らは、同時にベースラインとなるニューラルモデル(NAQANet)を提案しており、作成したデータセットでの性能がF1値で49.2%であることを示しています。人間による回答結果の精度が96.0%であることを考えると、自然言語処理において数値を扱うニューラルネットワークはまだまだ改善の余地があると主張しています。
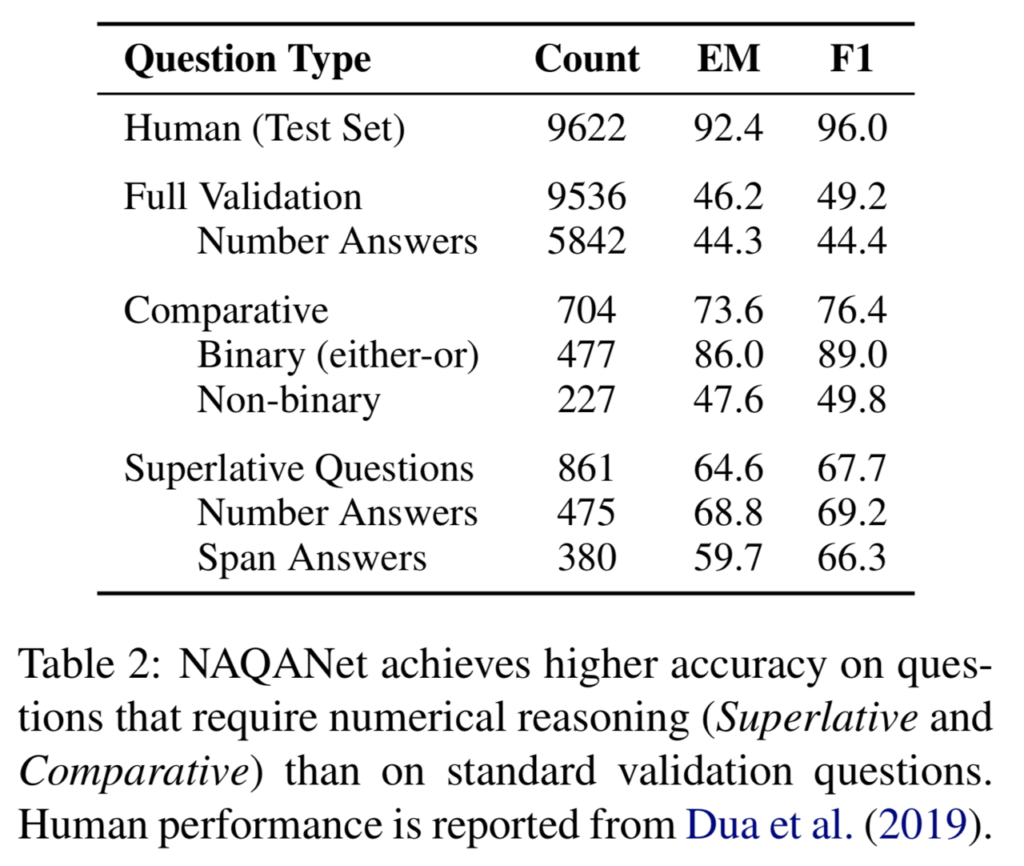
しかし、このデータセットに含まれる問題のうち「回答のために計算知識を必要とする問題」に限定すると、ニューラルネットワークによる回答の性能はむしろ良好であることが分かりました。具体的には、DROPデータセットのうち「数値の比較(comparative)」と「最大値の選択(superative questions)」のどちらかの計算知識を必要とする問題を選別し、それらに対するニューラルネットワークの性能を確認しました。
それぞれの計算知識を必要とする問題の例は上の表の通りで、例えば「(ある記事に対して)ブラジルとウルグアイではどちらの輸出額が多いか」という質問は、数値の比較をしたうえで(Comparative)二者から一つを選択する(binary)問題です。
また、「(ある記事に対して)20ヤード以上のタッチダウンをした選手は誰か」という質問は複数の選択肢から一つを選ぶ必要があるため、Non-binaryな質問としてbinary問題とは区別されています。
上記のように問題を区切った時、DROPのベースラインモデルであるNAQANetはComparativeな問題で76.4%、Superlativeな問題で67.7%のF1値であることが示されました。これは(人間の96.0%からは劣りますが)データセット全体の49.2%という数値と比較すれば決して悪くない性能であると言えます。このことから、DROPデータセットでニューラルネットワークの性能が低いのは、計算知識ではない別の数値的な問題が理由であると考えることができます。また同時に、ニューラルネットワークがこれまで考えられていた以上に計算知識を獲得できているということも分かりました。
単語分散表現は計算知識を学習できている?
ベースラインモデルはなぜ計算知識を必要とする問題を解くことができたのでしょうか。
これの答えとして筆者らは「QAタスクの学習のために事前学習した単語分散表現が、すでに計算知識を学習しているのではないか」と考えました。
QAタスクのようにニューラルネットワークを用いた自然言語処理の応用タスクでは、Word2VecやELMo、BERTなどのモデルを用いて単語分散表現を事前学習することが一般的です。これらのモデルで学習された単語分散表現が計算知識を含んでいるために、NAQANetは計算知識を必要とする問題を効率良く解くことができたと考えられます。
では、どのようにして「単語分散表現に計算知識が含まれているか」を調べたらよいでしょうか。その単語分散表現を用いて計算知識を必要とする単純なタスクを学習したとき、もし単語分散表現に計算知識が含まれているのであればランダムに初期化した単語分散表現よりも良い性能が得られるはずです。
そこで、事前学習された単語分散表現を用いて次の三つのタスクを学習し、その性能を比較してみます。
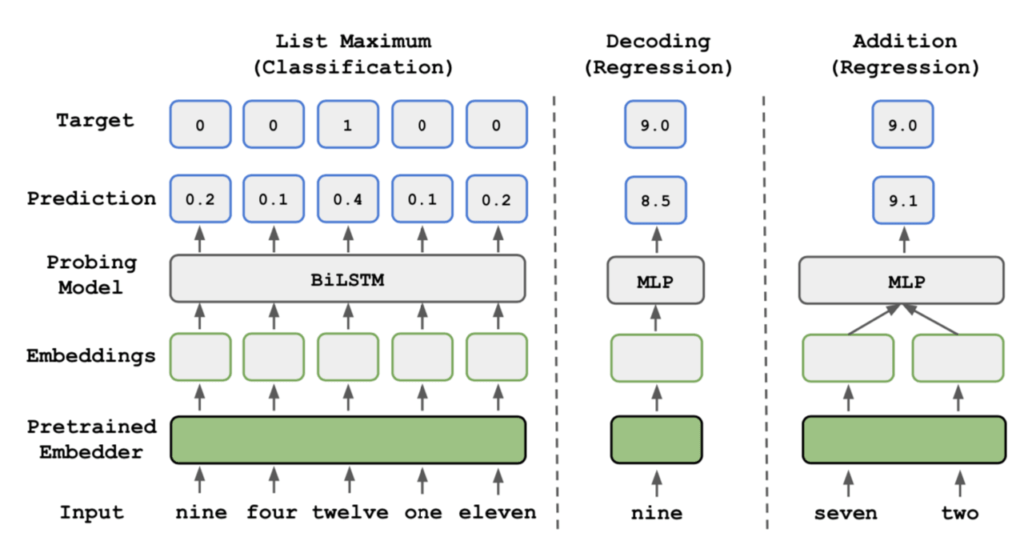
- 数値表現のリストから最大値を選択するタスク(List Maximum)
- 数値表現を、数値型に変換するタスク(Decoding)
- 二つの数値表現の足し算を行うタスク(Addition)
それぞれのタスクは、以下のモデルを用いて学習されます。例えば図右のAdditionタスクでは、文字で書かれた二つの数値表現「seven」と「two」の単語分散表現を入力とし、多層パーセプトロン(MLP)を用いて足し算の答えである9.0が出力となるような訓練を行います。この時、単語分散表現が計算知識を学習できているのであれば効果的な学習ができるため、その性能も高いものになると考えられます。
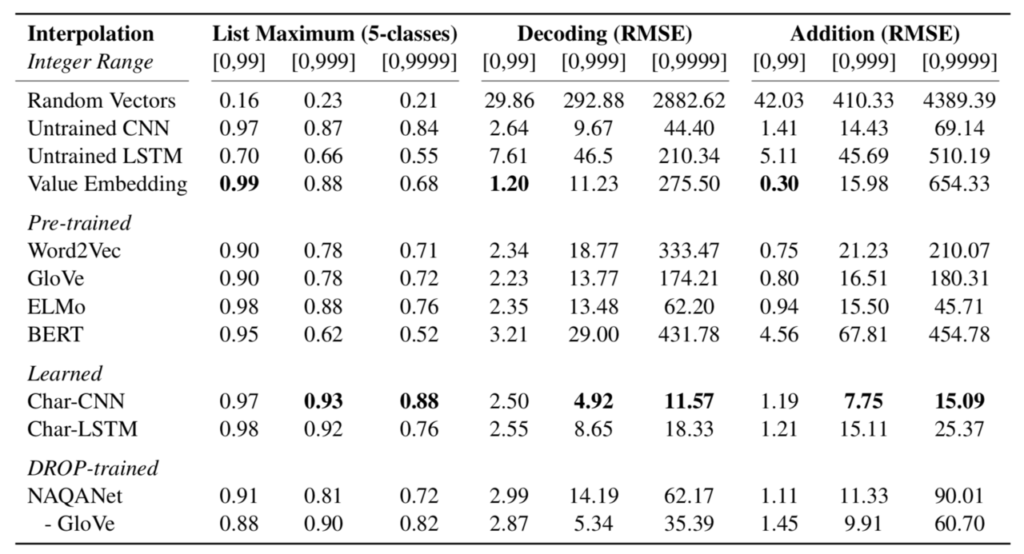
実験では上図における単語分散表現(Pretrained Embedder)として、有名なWord2Vec、GloVe、ELMo、BERTの四つを用いて比較します。下表は実験の設定と結果をまとめたもので、0~99、0~999、0~9999の三つの数値の範囲でそれぞれ学習・評価を行った数値が掲載されています。また比較のために、ランダムに初期化された単語分散表現(Random Vector)や、「seven」の単語分散表現を数値型の7として埋め込む方法(Value Embedding)での学習結果も掲載されています。
まず、ランダムに初期化した単語分散表現に比べて、ELMoやBERTなどの事前学習手法は精度よく各計算タスクをこなせていることがわかります。このことは、ELMoやBERTなどのモデルによって学習された単語分散表現がある程度の計算知識を獲得しており、さらに複雑な計算知識を要求するQAタスクにおいてもその知識を応用できることを示唆します。
一方で、単語分散表現の事前学習を行うモデル(Pre-trained)の中ではBERTの性能が著しく悪い点も特筆すべき傾向です。特に学習や評価に用いる数値の幅を大きくしていくことで、他の事前学習モデルに比べて激しく性能が低下していくことも確認できます。これはBERTがサブワードと呼ばれる単位で分割されたトークンを用いて学習しているためで、パターンの多い数値表現の全てを効率よく表現できていないことが原因であると考察されています。
このことを裏付けるように、文字レベルの情報を単語分散表現に盛り込んでいるELMoは、他の事前学習モデルに比べて性能が良いことが確認できます。さらに、文字の情報だけを使って各タスクの学習を行う「Char-CNN」や「Char-LSTM」という手法は安定して高い性能を示しています。これは数値の性質上、どの位置(桁)にどの数字があるかという情報を明示的に扱えるモデルの方が、数値の大小を扱いやすいという事実に起因していると考えられます。
まとめ
以上の実験から、本論文では事前学習された単語分散表現がある程度の計算知識を獲得していることを示しました。小さい数値と大きい数値は出現する文脈に差があるため、単語分散表現もそれを反映したものになるということは驚くことではありません。しかし、ランダムに初期化した単語分散表現と比べた時の性能の差や、単語分散表現ごとの差の大きさには目を見張るものがあります。
これまで多くのタスクに流用され有効であるとされてきたBERTが、計算知識の側面からはELMoなど従来の手法に劣ることという事実も、面白い結果といえます。一方で、文字レベルの情報を利用することで計算知識の獲得がスムーズになるという実験結果も、(数値の性質上当然ではありますが)示唆に富むものであると言えます。
また、ニューラルネットワークは学習データに含まれる範囲でしか計算知識を獲得できないことも分かりました。例えば本記事の最初に掲載した図では、学習範囲である-500~500を超えた入力に対しては、ほとんど正解の数値を当てられないことが示されています。
数値の取り扱いは、ニューラルネットワークをビジネスの現場に取り入れて行く上で障壁となる問題の一つと言えます。特に自然言語処理において数値を扱う場面は、間違うことが許されないような場面でもあります。今後こうした問題に取り組む際には、本論文で示された実験結果を参考にし、数値の特性をうまく捉えられるような単語分散表現を利用することが重要です。
Do NLP Models Know Numbers? Probing Numeracy in Embeddings
written by Eric Wallace, Yizhong Wang, Sujian Li, Sameer Singh, Matt Gardner
Accepted to EMNLP 2019
この記事に関するカテゴリー