学習をせずにCNNの精度がわかる?データセットの複雑度を測る新たな指標CSGの登場!
3つの要点
✔️CNNの精度と相関のある、データセットの複雑度である指標Cummulative Spectral Gradient (CSG)の提案
✔️CSGを用いることで、訓練データを大幅に削減可能
✔️従来手法と比較して、CSGはCNNの精度と高い相関
はじめに
近年、機械学習手法を評価するために、様々な大規模データセットが作成されています。最も有名なデータセットの1つはImageNetでしょう。このデータセットには1000クラス・1000万枚の画像が含まれています。このデータセットは画像分類のタスクを解く手法を評価するために作成されたものです。この他にも、多種多様なデータセットが作成され、評価に用いられています。
上記に述べたように、様々なデータセットが作成されていますが、データセットはどのような基準で作成されているのでしょうか。その1つの基準は「複雑度」です。つまり、現状の機械学習の手法では解くことが難しいデータセットを作成し、それをいかに解くかを、研究者たちは日々模索しています。
では複雑度とは一体何でしょうか?画像分類のタスクを例に取って、より深く考えてみましょう。
ここでは2クラスの画像が含まれるデータセットを作ると仮定します。この2クラスが、犬と猫であれば簡単に分類できることが期待できます。一方、アフリカゾウとアジアゾウは簡単には分類できそうにありません。つまり、画像分類タスクのデータセットの複雑度とは、クラス間がどれだけ似ているかということです。そして、クラス間の類似度を測ることで、データセットの複雑度が分かります。
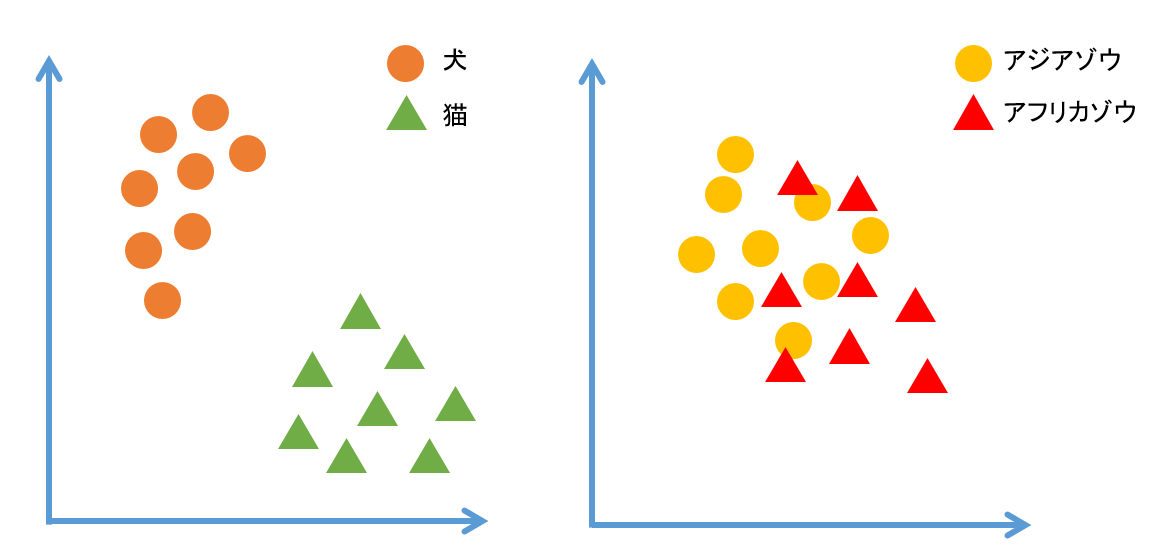
図1. クラス間の類似度
この複雑度を正確に計算することができれば、データセットのみから、機械学習手法で得られる分類精度が予測できます。
従来従来では、複雑度の計算時間はクラス数の三乗に比例していました。一方、提案手法であるCummulative Spectral Gradient (CSG)の計算時間はクラス数の二乗に比例します。例えば、クラス数が100であるデータセットの複雑度を計算する場合、計算時間を100分の1程度に削減できます。
さらにCSGは従来手法に比べて、深層学習手法での精度と非常に高い相関を持ちます。これは、正確にデータセットの複雑度を計算出来ているということです。
CSGを用いることで、学習を行う前から分類精度を正確に予測でき、さらに後で詳しく述べますが、分類精度を保ったまま訓練データを削減することが可能になります。これにより、学習時間を大幅に削減することが可能となり、より効率的にモデルを学習できます。
提案手法
では、提案手法であるCSGの計算方法を詳細に見ていきましょう。大きく分けて、CSGの計算には以下の3つのステップがあります。
(1) クラス間の類似度を計算する。
K個のクラスから構成されるデータセットの場合、K×Kのクラス間類似度行列を作成する。
(2) (1)で作成した行列から、データセットの複雑度を計算する。
複雑度は行列の固有値と密接な関係があり、複雑度が低いデータセットは小さい固有値を持ち、複雑度が高いデータセットは大きな固有値を持つ。
(3) (2)で計算した固有値の勾配を利用して、CSGを計算する。
では、この3つのステップをより詳細に見ていきましょう。
(1)クラス間類似度の計算
(1)では、各クラス間の類似度を計算しています。ではどのように類似度を計算すれば良いでしょうか。
提案手法では、各クラス間の分布の距離を類似度として計算しています。分布の距離を計算する手法はいくつか存在しますが、ここでは、以下のような式によって距離を計算しています。
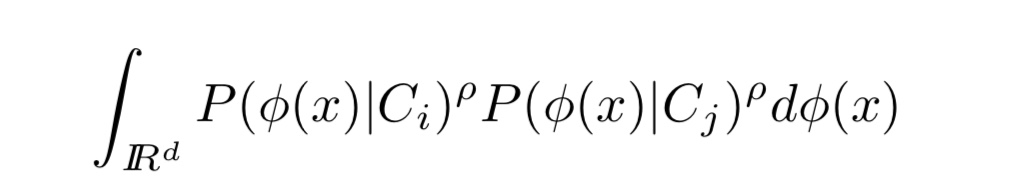
式1. 分布間の距離
ここで$x$は入力画像の生データ、$Φ$は$x$を次元の異なる空間に写像する関数、Ciは入力画像のクラスを表しています。
式(1)のように、各クラスの確率分布の積をとることで分布間の距離を計算することができます。2つの正規分布を想像すると理解しやすいかも知れません。それぞれの分布が被っていると、式(1)はゼロより大きくなり、全く被っていないとゼロとなります。なお、提案手法では$ρ$=1としています。
ここで、式(1)をよく見ると、これは以下の式と同等であることが分かります。
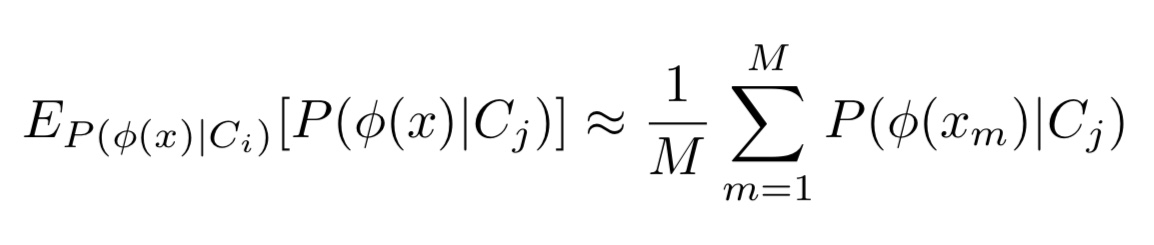
式2. 式1の近似計算式
さらに、期待値計算はある確率分布に基づいて、サンプリングを行い、それらの平均をとることで近似できます。上記の操作により、クラス間の類似度を計算することができます。また、以下の図をご覧下さい。
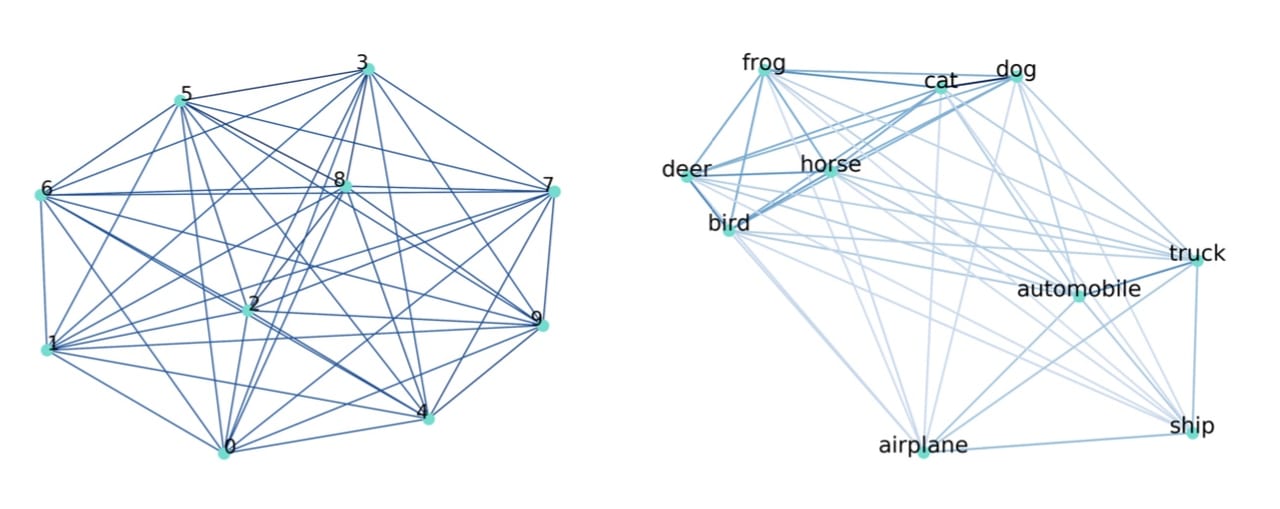
図2. (左)mnist (右)CIFAR10 のクラス間の類似度
図2はクラス間類似度を表した図です。各クラス間が近ければ近いほど、そのクラス間の類似度が高いことを示しています。mnistは各クラスがしっかりと分離していますが、CIFAR10はdeerとbirdなど、類似度が大きいものがいくつか存在しています。
(2) 複雑度を表す値の抽出
(2)では、(1)で計算したクラス間類似度を表す行列からデータセットの複雑度と関係する値を計算します。ここで用いられるのが、spectral clustering理論と呼ばれるものです。詳細は割愛しますが、大まかには以下のような手順で、複雑度と関係する値を計算します。
(ⅰ) (1)で計算したクラス間類似度行列Wを計算する。また、Wの各列ごとに和を取った対角成分のみが存在する行列Dを計算する。
(ⅱ) L = D-Wを計算する。
(ⅲ) Lの固有値を計算する。
この行列Lは0を含む、クラス数と同じ数の固有値を持つことが知られています。そして、Lが疎な行列(0に近い値で構成されている行列)の場合、この固有値が小さくなり、Lが密で大きな値で構成されている行列の場合、固有値が大きくなることが知られています。つまり、固有値が小さい時、クラス間類似度が小さく、データセットの複雑度が低いことを表しています。一方、固有値が大きいとき、クラス間類似度が大きく、データセットが複雑であることが分かります。
(3) 固有値を用いたCSGの計算
(2)で述べたように、クラス間類似度行列から作られた行列Lの固有値はデータセットの複雑度と密接な関係があります。また次のグラフをご覧下さい。
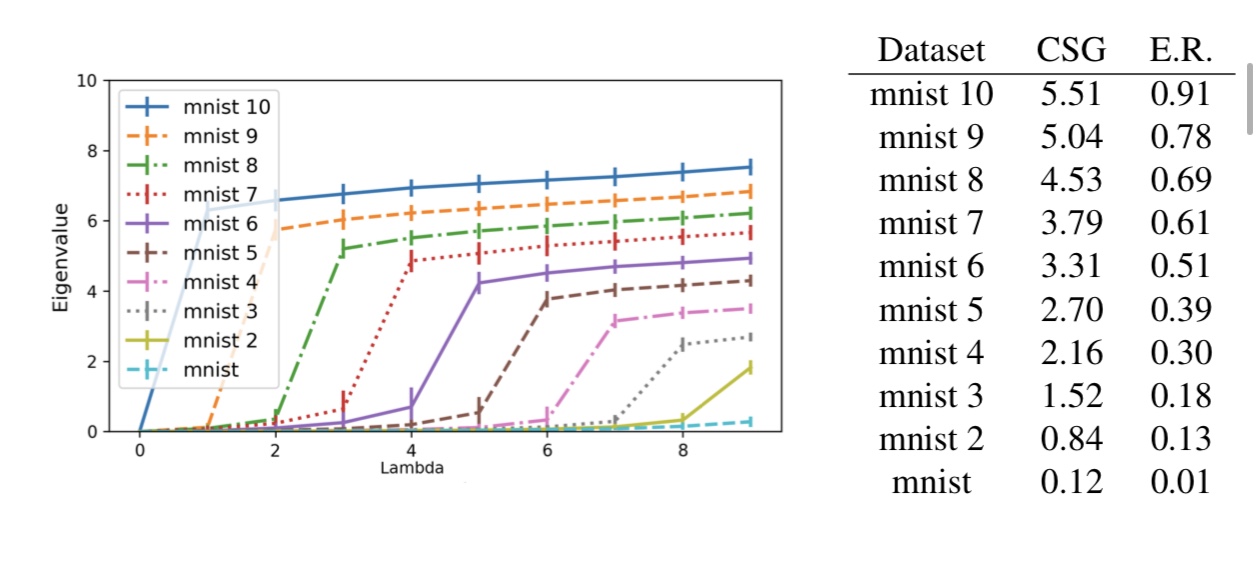
図3. 固有値の大きさとデータセットの複雑度の関係
図3はmnistと呼ばれる0〜9の手書き数字データセットを用いて、行列Lの固有値を左から昇順に表した結果です。縦軸が固有値の大きさを表しています。ここで、mnist K はmnistの任意のK個のクラス間の画像をランダムに入れ替えたデータセットを表しています。つまり、Kが大きくなるにつれ、データセットの複雑度が増すことが予想されます。
また、図3によると、複雑なデータセットほど、早い段階で固有値の勾配(固有値の差分)が大きくなっていることが分かります。
上記の議論を踏まえて、提案手法ではデータの複雑度を計算する指標を以下のように定義しています。

式3. CSGの定義式
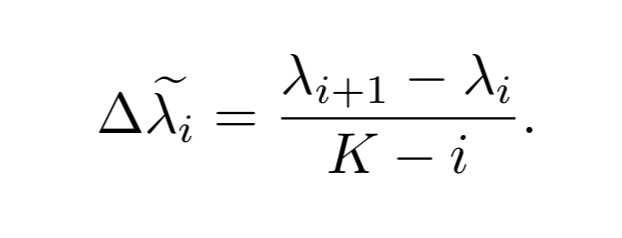
ここで、K-iは固有値の勾配の最大値であることが知られており、$Δλ$の値を0〜1に制限する正規化の役目を果たしています。
また、cummaxとは累積最大値を取る操作です。これは、あるベクトル$v$=(3, 5, 2, 7, 1)というベクトルがあった時に、cummax($v$)= (3, 5, 5, 7, 7) とする操作です。つまり、cummaxのi番目の値はcummaxの1からi-1番目の値と、元のベクトルのi番目の値の中で最大のものとなります。最初の方に最大値があれば、その後のcummaxの要素は全てその最大値となります。
式3のように定義された指標CSGは、固有値の値が大きく、かつ、早い段階で勾配が大きくなると、値が大きくなります。
実験結果
では、ここからはCSGを使った様々な実験の結果を見ていきましょう。
実験条件
まず、使用するデータセットは以下の10種類です。
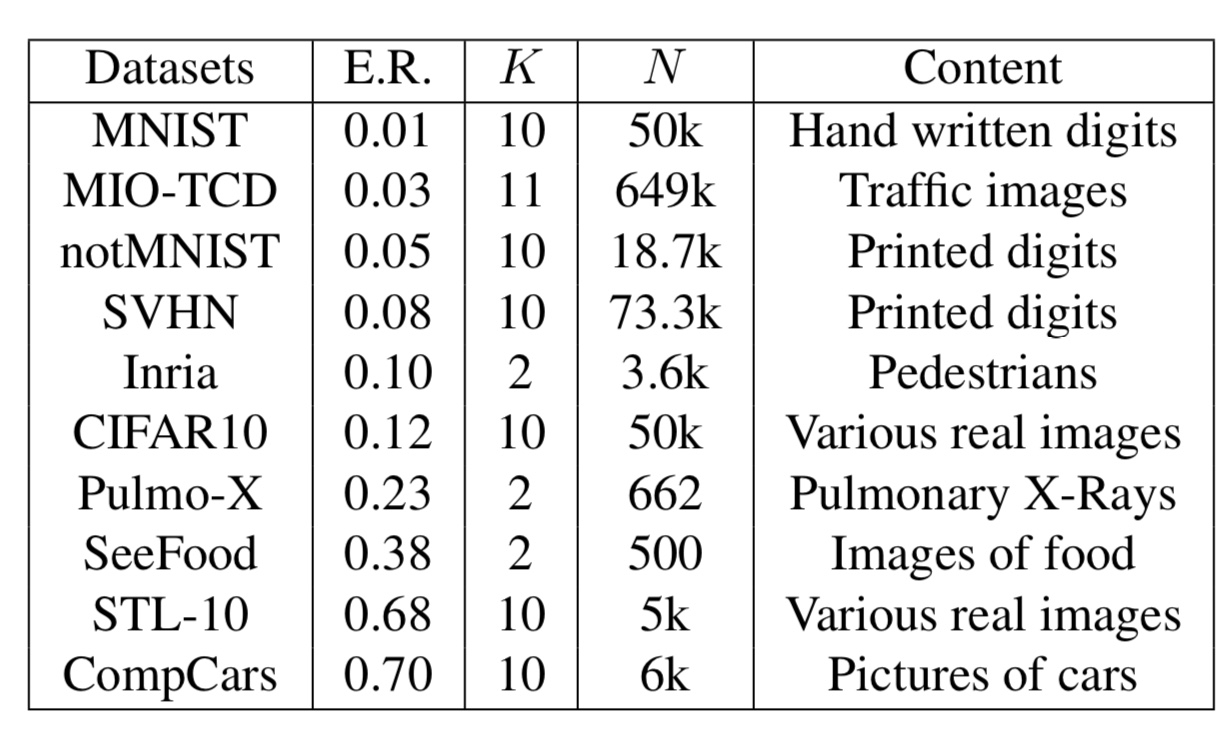
図4. 実験に使用するデータセット一覧
ここで、E.R.はAlex Netでの分類エラー率、Kはクラス数、Nは画像数を表しています。
また、類似度を計算するときに用いた関数$Φ$は以下の4種類です。
1. RAW : $Φ(x)=x$
2. t-SNE : 生画像を二次元に落とし込む関数
3.CNNAE : 9層のCNNオートエンコーダー
4. CNNAE t-SNE : 3から得られる特徴量をt-SNEで二次元に落とし込む関数
CSGと画像分類モデルのエラー率の相関
この記事では、図4のデータセットのうち、クラス数が10であるものを使用して、従来手法とCSGを比較する実験のみを紹介します。なお、使用した画像分類モデルはAlex Netです。実験結果は以下の通りです。
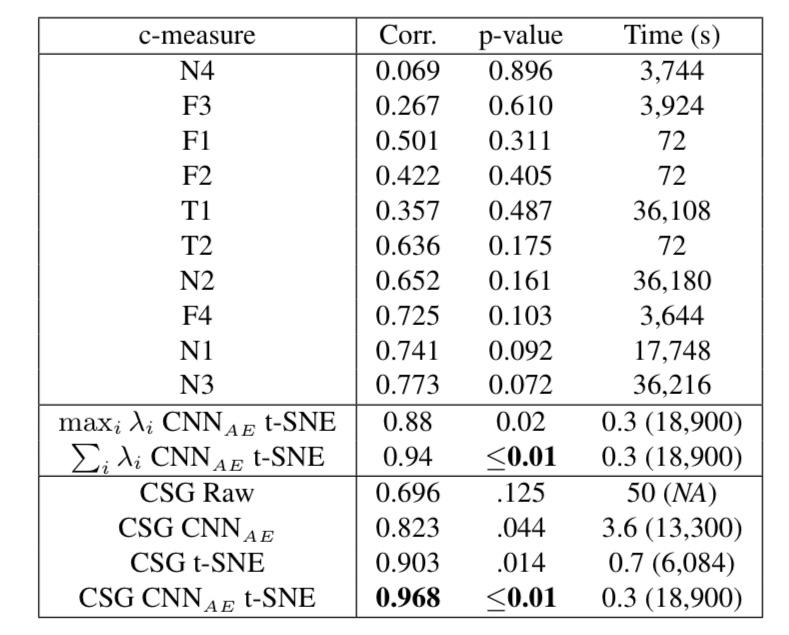
図5. 従来手法とCSGの比較実験
図5の下4つがCSG、下から6番目は行列Lの固有値の最大値、下から5番目は固有値をプロットした時に描かれる曲線の下側の面積を用いて複雑度を計算した場合の実験結果を表しています。その他は、すべて従来手法での結果です。
また、Corr.は画像分類モデルのエラー率との相関係数を、p-valueはp値(計算結果の信頼性に関わる値。小さいほど、計算結果が偶然出たものではないことを示す)を表しています。
図5によると、CSGは画像分類モデルのエラー率と非常に高い相関があり、かつ、計算時間が非常に短いことが分かります。
この実験結果をより詳細に表したのが、以下の図6です。
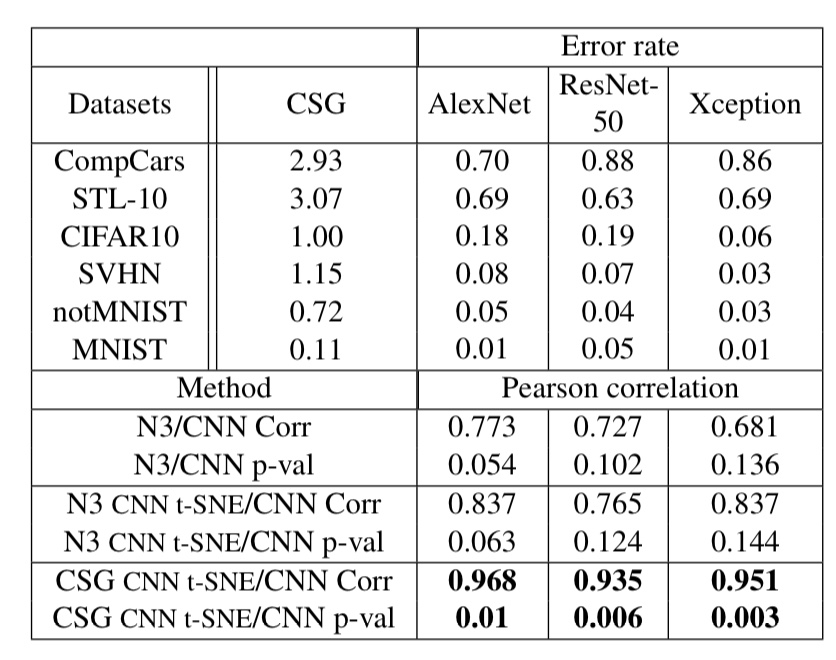
図6. 図5の詳細結果
図6では、Alex NetだけではなくResNet-50とXceptionを用いて、実験を行なっており、3つのモデルのエラー率とCSGが非常に高い相関を示していることが分かります。
CSGを用いたデータセット削減
冒頭でも述べましたが、CSGは訓練データの削減に用いることができます。これは訓練データを削減しながら、その削減されたデータを用いてCSGを計算することで実現できます。つまり、CSGとエラー率には非常に高い相関があるため、CSGが高くならない所までは、訓練データ数を削減することが可能となります。
ここでは、MioTCDと呼ばれる大規模なデータセットを用いて実験を行います。実験結果は以下の通りです。
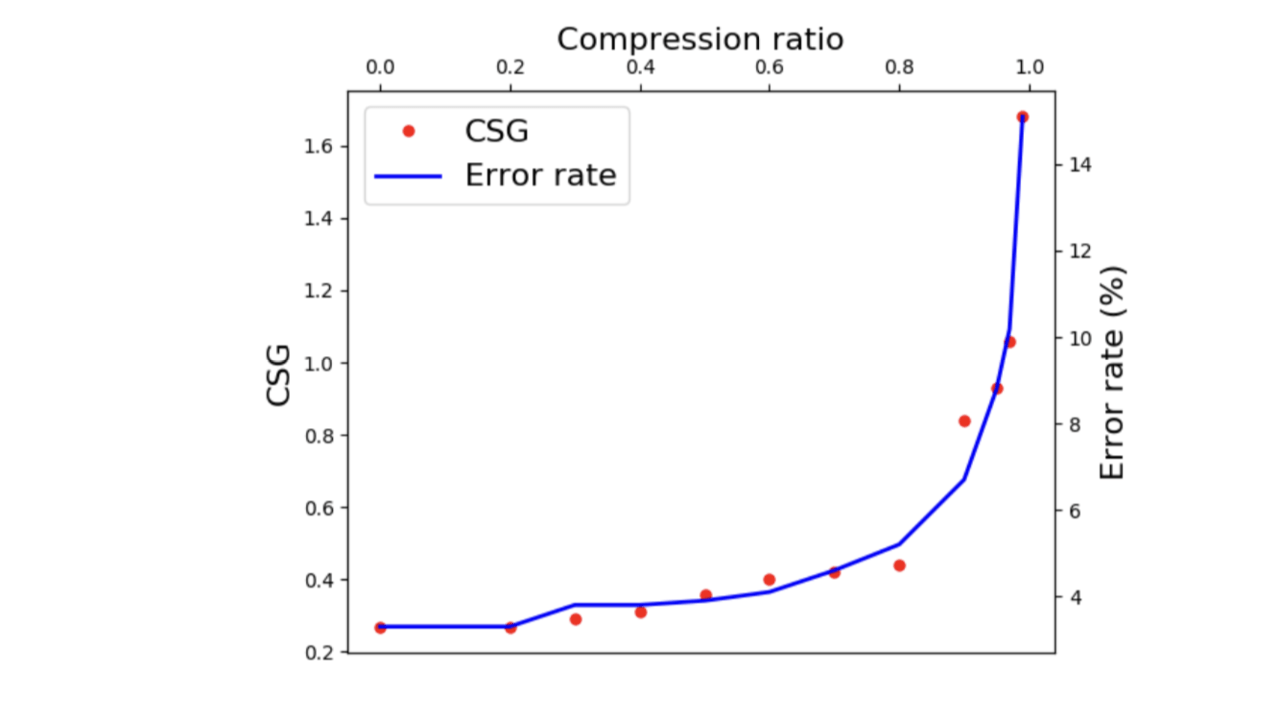
図7. CSGを用いた訓練データ削減
図7によると、訓練データを80%削減しても、CSGがほとんど変化していないことが分かります。これは、訓練データを80%削減しても、分類精度を保つことが可能であるということを示しています。
まとめ
本記事では、データセットの複雑度を計算する新たな指標CSGを紹介しました。CSGは従来手法と比較して、複雑度を高速に、かつ高精度に計算することができます。これによって、学習を行う前から分類精度を高い精度で予測することが出来ます。
また、CSGを用いることで訓練データをどこまで削減できるか判断できるようになりました。大量のデータを用いて学習を行うと、学習時間も長くなりますし、大量のメモリを確保しておく必要があります。学習を行うまえに、CSGを用いて、訓練データの削減を行うことで、効率よくモデルを学習することができます。
本研究では、画像分類タスクのみに焦点を当てていますが、これが物体検出やセグメンテーションにまで応用可能になれば、より効率的にAIモデルの学習が行えると思われます。
個人的には、画像認識タスクのみだけではなく、自然言語処理タスクまで応用可能だと考えています。なぜなら、CSGはクラス間の類似度計算を変えるだけで、その後の手順は変わらないからです。
この研究をきっかけに画像認識や自然言語処理などの分野でデータセットの複雑度を計算する研究が盛んになることを期待しています。
Spectral Metric for Dataset Complexity Assessment
written by Fre ́de ́ric Branchaud-Charron et.al.
(Submitted on 20 May 2019)Accepted by CVPR 2019
Subjects: machine learning (cs.LG)
この記事に関するカテゴリー








