最適な学習済みモデルが分かる?転移学習を加速させるTASK2VECの登場!
3つの要点
✔️タスク(データセットとラベルの組み合わせ)をベクトル化するTASK2VECの提案
✔️タスク間の類似度を計算することにより、どの学習済みモデルを使えば良いか判断可能に
✔️様々なタスクでの実験で、TASK2VECは最適に近い学習済みモデルを予測することに成功
はじめに
転移学習をご存知でしょうか。これは学習済みモデルを再利用することにより、少ないトレーニングデータでも、性能を発揮できる学習方法です。
転移学習の例としては、ImageNetによるものが最も有名でしょう。これは画像分類のタスクを行う際に、ImageNetで学習したモデルの最終層(分類を行う層)だけを、解きたいタスクに応じて再調整する、というものです。
このような学習が上手くいく理由の1つに、ImageNetでの学習によって、良い画像特徴量を抽出する機構が出来上がっているからです。その機構を再利用すれば、トレーニングデータが少なくとも、上手く学習出来ることが予想されます。
トレーニングデータが少ない場合に、大きな効力を発揮する転移学習ですが、どの学習済みモデルを再利用すれば良いのでしょうか?これはメタ学習という枠組みで盛んに研究が行われています。
メタ学習は、学習プロセスを学習する手法です。今回の場合においては、どの学習済みモデルを使うと、より良い精度が得られるかという問題に置き換えることが出来ます。
今回紹介する論文では、TASK2VECと呼ばれる手法により、上記の問題に対してアプローチしています。TASK2VECでは、フィッシャー情報行列(FIM)と呼ばれる、タスクに関する情報を含んだものを利用して、タスクをベクトル化しています。FIMに関しては、後ほど説明させて頂きます。
このベクトル化したタスクを用いて、タスク間の類似度を計算し、どの学習済みモデルを使えば良いか予測しています。
実験の結果、TASK2VECを用いた手法により、最適に近い学習済みモデルを予測することに成功しています。図1は本論文の目的を表した図です。
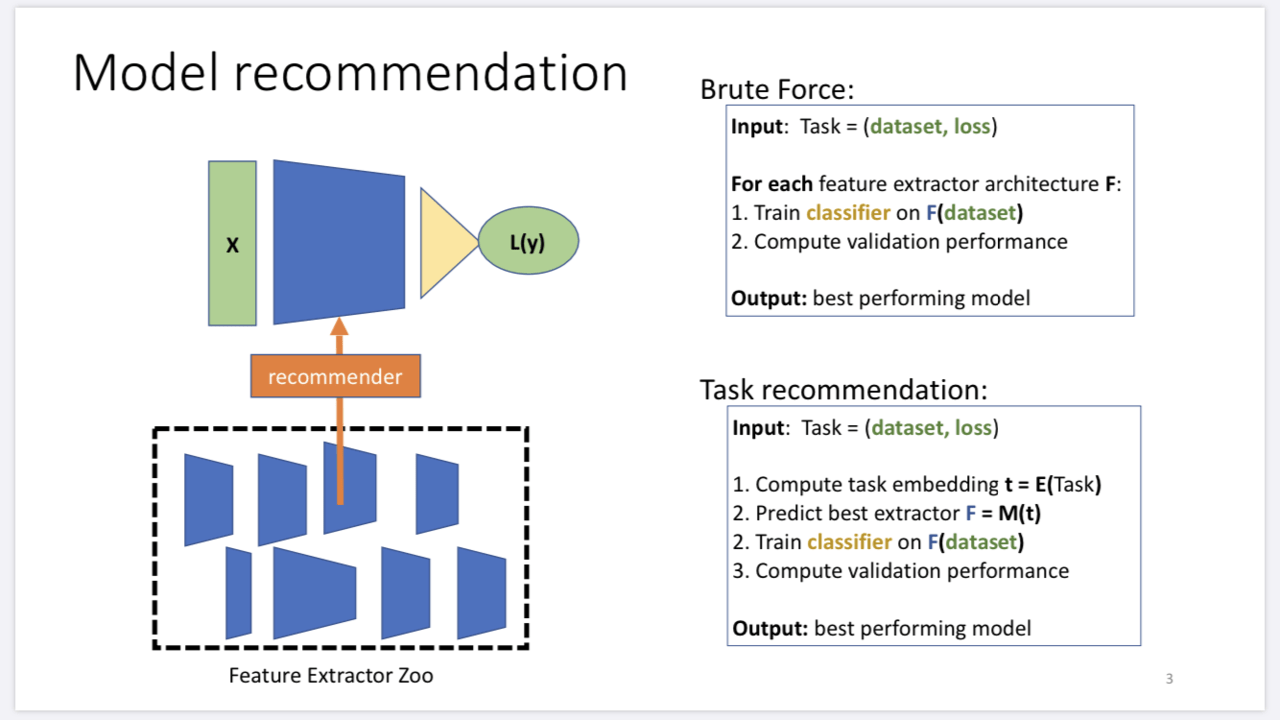
図1. 本論文の目的
TASK2VEC
まず、タスクをベクトルにするTASK2VECの手順を見ていきましょう。TASK2VECには大きく分けて2つのステップが存在します。
1. 学習済みモデルの出力からフィッシャー情報行列(FIM)を計算する。
2. FIMの対角成分のみを取り出す。対角成分のうち、同じフィルタでの値を平均して、固定長のベクトルを出力する。
TASK2VECは上記のステップによって、タスクを固定長のベクトルに変換します。では、それぞれのステップについて、詳しく説明していきます。
FIMの計算
タスクを解くためには、入力$x$とそれに対応するラベル$y$の関係pω(\(y|x)\)を学習する必要があります。ここで$ω$は学習によって得られるパラメータです。
タスクを解くためにこのパラメータ$ω$はどれ程有益なものなのでしょうか。それを測るために、$ω´$=$ω$+$δ$$ω$ と学習したパラメータを少しだけ変化させたパラメータを考えます。pω(\(y|x)\) とpω´(\(y|x)\) がどれだけ異なるのか、計算し、大きく異なるようであれば、そのタスクはパラメータに大きく依存しているということが分かります。pω(\(y|x)\)とpω´(\(y|x)\)がどれだけ異なるのか、計算する指標として、KL divergenceと呼ばれるものがあります。このKL divergenceを近似する以下の式が導出されます。
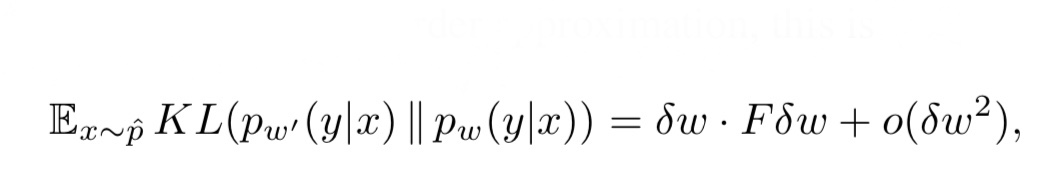
式1. KL divergenceの近似式
ここで、右辺のFはフィッシャー情報行列(FIM)と呼ばれるものです。FIMは以下の式で表されます。
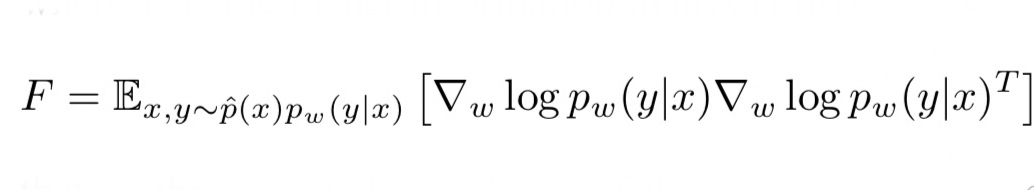
式2. FIMの定義式
FIMは確率分布の各パラメータごとの勾配を計算し、その転置行列との積をとっています。確率分布はベクトルで、それをパラメータベクトルで微分すると行列となります。この時、行列のi行目は確率分布の全ての値を、i番目のパラメータで微分したものとなります。つまり、FIMの対角成分のみが、同じパラメータで微分したものの二乗が並びます。(二行二列の行列で考えてみると分かりやすいと思います)
これは、FIMが小さい値だと、タスクは大きくパラメータに依存していないということになります。また、以下の式をご覧ください。これは、二層のニューラルネットワークの場合、FIMは以下の式で表されます。(式の導出に興味のある方は原論文を参照して下さい)
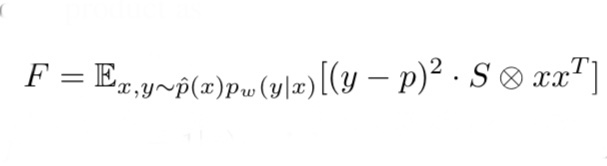
式3. 二層ニューラルネットワークのFIM
式3は予測ラベルと正解ラベルの差が小さいほどFが小さくなることを表しています。つまり、FIMの大きさはタスクの複雑度にも関係があります。本論文では、上述の理由からFIMをタスクを表す指標とします。
このFIMを計算する際に、異なるネットワーク構造を利用すると比較が出来なくなるため、本論文ではどのFIMの計算においても単一のモデル(以下ではprobe networkと呼ぶ)を使用します。probe networkはImageNetで学習し、その後、各タスクに応じて最終層だけを再調整したものです。
効率的なFIMの計算
式2をみると、FIMは全てのパラメータに対しての勾配を計算する必要があり、非常に計算するのが大変です。そこで、本論文では2つの仮定を置き、効率的にFIMを計算しています。
【仮定1】: probe networkの異なるフィルタ間の相関は重要ではない。
【仮定2】: 同じフィルタ間の値は相関がある。
仮定1から、FIMの対角成分のみを計算すれば良いことになります。また、仮定2より、対角成分のうち、同じフィルタ間の値は相関があるため平均化を行います。最終的に出来あがるベクトルはフィルタの数と同じになります。ここで、単一のprobe networkを使用していることから、すべてのタスクを固定長のベクトルに落とし込むことが出来ます。
上述したように、FIMの大きさとタスクの複雑度には関係があり、上記のように作られたベクトルの大きさもタスクの複雑度と関係します。
この手順により作られたベクトルを使って、タスク間の距離を計算していきます。
タスク間の距離の計算
本論文では、タスク間の距離を計算する指標を2つ提案しています。
1. コサイン類似度で計算(対称性を持つ)
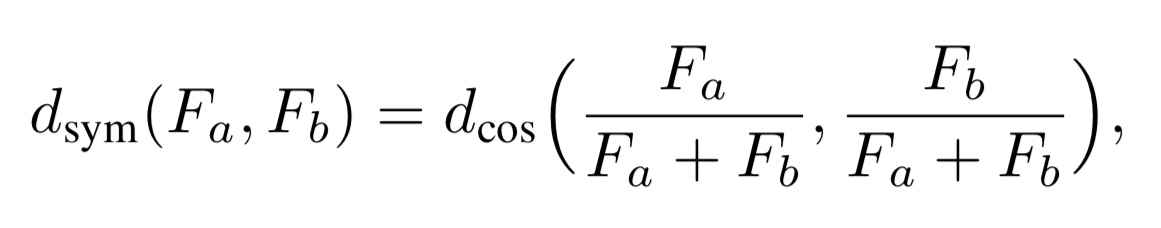
式4. 対称なタスク間距離の指標
ここで、FaとFbはタスクaとタスクbをTASK2VECによってベクトル化したものです。
2. 非対称な類似度で計算
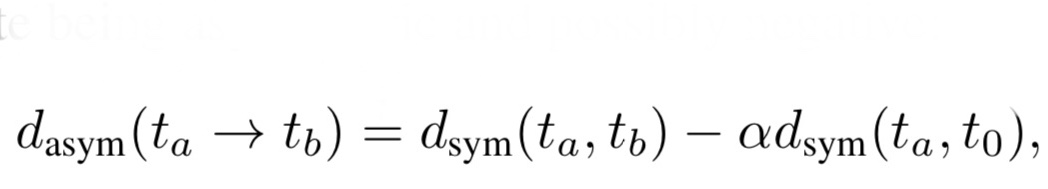
式5. 非対称なタスク間距離の指標
経験的に、 ImageNetのように複雑なデータセットで学習したものは、学習済みモデルとして良い性能を発揮します。つまり、タスクaを用いて学習して、それをタスクbに転移学習させる際には、タスクaが複雑であればあるほど、良い結果が得られることが予想されます。
そこで、基準となる簡単なタスクt0とタスクaとの距離を計算し、それが0に近いほどタスクaは複雑となります。
つまり、式5はタスクaとタスクbの類似度が高く、かつ、タスクaとタスクt0の類似度が低いほど大きくなる指標です。
MODEL2VEC
ここまでは、タスクのみに焦点を当ててきました。しかし、モデル自身も有益な情報を含んでおり、タスクとモデルの性質を組み合わせてベクトル化することで、より精度の高いモデル選択が行えることが予想されます。
そこで、本論文ではk個のモデルが与えられた時に、最適なモデルを選択するように以下の式中のbiを学習します。
$mi=Fi + bi$
この$mi$を用いてモデル選択を行います。このようにモデルとタスクを合わせてベクトル化する手法をMODEL2VECと呼びます。
実験結果
ここからはTASK2VECによってタスクをベクトル化したものを使用し、数多くの学習済みモデルの中から、どれを選択すれば良い精度が得られるかの実験結果を見ていきましょう。
使用データセット
・iNaturalist : それぞれのタスクは種の分類タスクに対応しています。例えば、Rodentiaタスクはネズミなどの齧歯類を分類するタスクです。207のタスクが存在します。
・CUB-200 : 全てのタスクは鳥種の分類です。25のタスクが存在しています。
・iMaterialist : 服の分類に関するタスクです。例えば服の色や素材を分類するタスクが含まれています。228のタスクが存在します。
・DeepFashion : iMaterialistと同じタスクから構成されています。1000のタスクが存在します。
4つのデータセット合わせて、合計1460のタスクで実験を行なっています。
学習済みモデル
使用するモデルはResNet-34をImageNetで学習し、その後fine-tuningしたものと、fine-tuningを行わない2つのパターンを試しています。
ここで、fine-tuningは、全てのタスクで行うのではなく、関連したものはまとめて行うなどしているため、合計156の学習済みモデルを使用します。
この中から最適な学習済みモデルをTASK2VECを使用して予測する実験を行っています。
ベクトル化したタスクの可視化
以下の図2をご覧ください。これはiNaturalistとiMaterialistの各タスクをベクトル化したものを二次元に落とし込んで、可視化したものです。
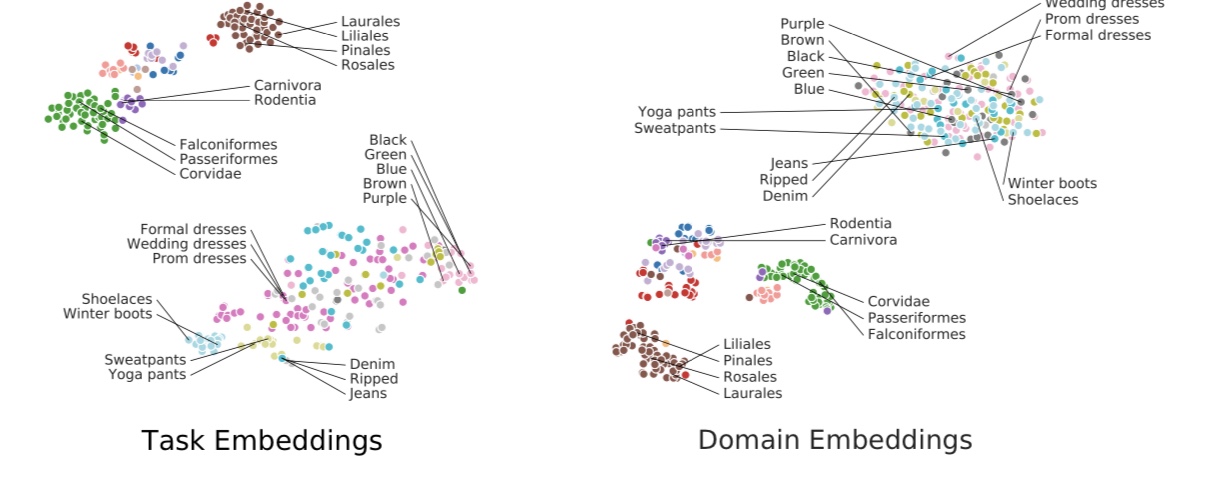
図2. タスクの可視化
左がTASK2VECを利用してベクトル化したもの(Task Embedding)を、右が入力$x$だけを利用してベクトル化したもの(Domain Embedding)を表しています。どちらの場合でも、データセット間は分離していますが、Domain Embeddingでは、iMaterialistのタスクは1つのクラスタとしてまとまっています。これはデータセット内のタスクを分離出来ていないことを示しています。
学習済みモデル選択実験
図3をご覧下さい。これは156の学習済みモデルから特徴量を抽出し、それを元に分類器を学習した時の分類誤差を表した図です。
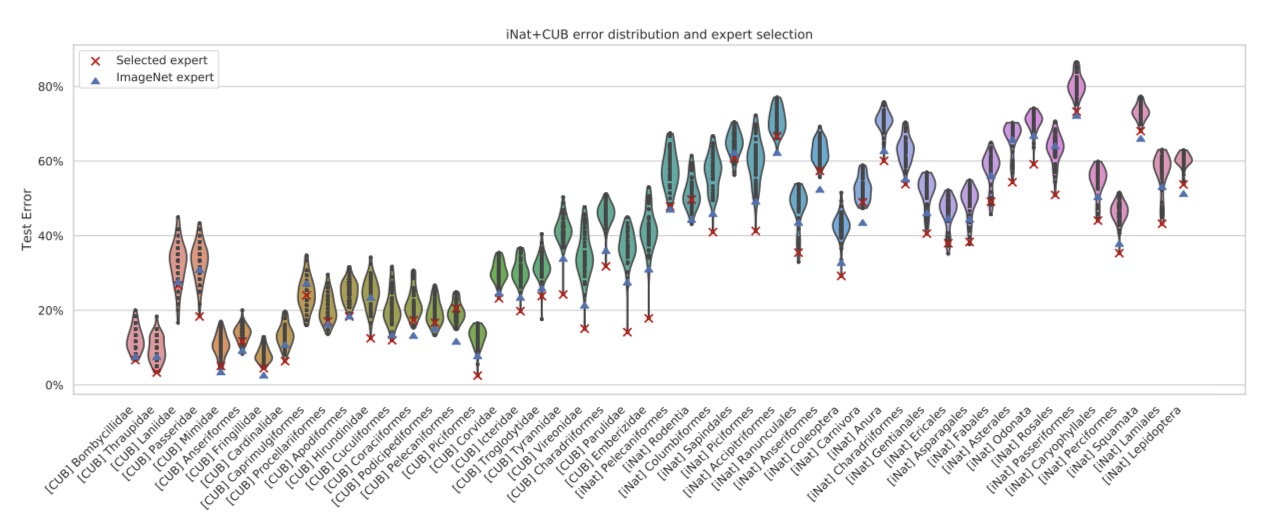
図3. タスクの分類誤差とモデル選択
縦軸は分類誤差、横軸はタスクを示しています。なお、タスクはベクトルの大きさが小さいものを左から順に並べています。青の△がfine-tuningをしていないimagenetで学習したものから特徴量を抽出した時の分類誤差、赤の×はTASK2VECを利用してモデル選択を行った場合の分類誤差です。
まず、グラフが右に行くに従って、分類誤差が大きくなっています。これはタスクの複雑度が右に行くほど高くなっていることを示しており、TASK2VECによって得られるベクトルの大きさは、タスクの複雑度と正の相関があることが分かります。
そして、タスクの複雑度が低いうちは青の△と赤の×にはそれほど違いはありません。しかし、タスクの複雑度が高くなるにつれ、赤の×(TASK2VECによって選択したモデル)が最適に近い分類結果を残すようになっています。
また、以下の表をご覧ください。

表1. タスク間距離の測り方によるモデル選択精度の変化
表1によると、ImageNetのみで学習した特徴量抽出器はランダムに選択したものよりも良い精度を発揮していることが分かります。しかし、TASK2VECを用いて、タスク間の距離を測定し、モデル選択を行った場合は、それ以上に最適に近いモデル選択を行えています。
まとめ
本記事では、タスクをベクトル化する手法TASK2VECの紹介をしました。TASK2VECによってベクトル化したものは、タスクに関する有益な情報を含んでいます。これを用いることで、タスク間の類似度を計算することができ、転移学習を行う際に、どのモデルを選択すれば良いか高い精度で予測出来るようになりました。
深層学習を実応用するにあたって、まず立ちはだかる壁は教師データの収集です。転移学習は少ない教師データで、性能を発揮できる手法であり、本論文のような学習プロセスを学習するメタ学習の重要性は増していくと考えられます。
自然言語をベクトル化するword2vecは非常に有名ですが、タスクのような、概念的なものをベクトルにするというのは画期的な研究だと個人的には思います。この記事をきっかけに、メタ学習に興味を持って頂ければ幸いです。
Task2Vec: Task Embedding for Meta-Learning
written by Alessandro Achille, Michael Lam, Rahul Tewari, Avinash Ravichandran, Subhransu Maji, Charless Fowlkes, Stefano Soatto, Pietro Perona(Submitted on 10 Feb 2019)
Subjects: Machine Learning (cs.LG); Artificial Intelligence (cs.AI); Machine Learning (stat.ML)
この記事に関するカテゴリー








