相似向量搜索的SoTA！介绍ScaNN，一种用于GCP：顶点匹配引擎的方法。

矢量搜索 04/06/2021

三个要点
✔️关于GCP新产品顶点匹配引擎的原创论文
✔️提出一个新的量化损失函数，考虑到MIPS的分数
✔️ ANNBenchmarks上创纪录的SoTA性能

Accelerating Large-Scale Inference with Anisotropic Vector Quantization
written by Ruiqi Guo, Philip Sun, Erik Lindgren, Quan Geng, David Simcha, Felix Chern, Sanjiv Kumar
(Submitted on 27 Aug 2019 (v1), last revised 4 Dec 2020 (this version, v5))
Comments: Published as a conference paper at ICML 2020.
Subjects: Machine Learning (cs.LG); Machine Learning (stat.ML)

code：

首先

ScaNN是由谷歌宣布的，以加快相似性矢量搜索的速度。著名的标杆网站"ann-benchmarks.com"，这也是记录了最先进性能的方法。有一天。GCP。顶点匹配引擎它以极高的性能实现了相似性向量搜索，最近在GCP上发布了（预览版）。由于这是一个高调的产品，我想借此机会介绍一下原始论文。

相似性向量搜索可以应用于各种服务，并经常与机器学习结合使用。然而，如果你看一下顶点匹配引擎的文档，你会发现它可以承受巨大的数据规模和QPS，所以我个人很期待顶点匹配引擎。

类似的矢量搜索

相似性向量搜索（也叫近邻搜索）已成为解决大规模分类和搜索任务的一种流行技术。特别是，它已经成为一种非常通用的技术，因为机器学习模型将数据映射到一个嵌入空间，使我们能够回答以前难以回答的抽象查询（如下图所示的流量）。例如，它可以应用于推荐类似的产品、类似的图像和类似的文件。

实现近邻搜索的一个常用方法是使用内积距离的最大内积搜索（MIPS）。MIPS的问题可以正式定义如下。

考虑一个有$n$数据点的数据库$X={x_i}, i=1,2,...,n$。每个数据点都在一个维度为$x_i \in R^d$は$d$的向量空间中。这里，给定一个查询$q \in R^d$，任务是确定与$q$有最大内积的数据点$x \in X$，即

$$x_i^* := arg max \left< q, x_i \right>$$

在这里，由于数据库通常很大，详尽地计算查询$q$和所有数据点的内积（$mathcal{O}(Nd)$，数据数量为$N$，矢量维数为$d$）往往是不现实的。因此，即使数据点不是严格意义上的近邻，一般也会采用能加快搜索速度的近似近邻搜索，各种研究中都提出了基于散列、图搜索、量化等技术。

MIPS效率

开发一个高效的MIPS系统有两个主要挑战。

减少与查询比较的数据点的数量
- 树状结构、图形、使用哈希函数（保持相似性）的空间划分，以及其他方法
- 只与给定查询相关的子空间中的数据进行比较
数据点的压缩
- 矢量量化方法是最先进的方法。
- 压缩提供了各种好处，如减少内部产品的计算，通过减少内存使用提高资源效率，以及减少存储。

如上所述，已经提出了各种方法来处理这些问题。作者的贡献在于量化部分，他们提出了一个量化损失函数，不仅考虑了速度方面，还考虑了MIPS的精度，这是新的。

在下文中，我们首先描述量化，如果你已经知道了，你可以跳到作者提出的方法部分。

矢量量化

以直积量化为例，它是矢量量化的一般方法，量化的基本思路和程序可以简要说明如下。

(准备) 建立编码簿
- 将矢量分成$M$部分，并将它们视为$M$的$d/M$维矢量
- 计算数据库中的数据点的k-means
(准备) 使用编码本对数据库中的所有数据点进行量化
- 从一个$d$的浮点型向量压缩到一个$M$的uint型向量
- $32 \times d$ bit $\rightarrow$ $8 \times M$ bit
(在查询时) 对查询数据进行量化，并从数据库的PQ代码中进行搜索

给定一个查询向量，量化后的图像如下图所示。在这一步中，我们还记录了查询和每个密码字之间的距离表。

量化后，所有步骤中计算出的距离表被用来从数据库中的PQ码组中线性地搜索出最接近的距离。

这使得原本需要花费$mathcal{O}(Nd)$并且在大规模上不切实际的搜索问题，以更少的计算量变得可行，$mathcal{O}(dK+MN)$。

建立一个编码簿

在这一节中，我们描述了初步准备工作，即编码簿的构建。编码选择中的优化问题可以表述如下。

$min_{c_1, c_2, \cdots, c_k \in \mathbb{R}^d} \sum_{x_i} min_{\tilde{x_i} \in \{c_1, c_2, \cdots, c_k\}} ||x_i - \tilde{x_i}||^2$

这实际上与k-means中解决的优化问题形式相同，并且它可以通过与K-means相同的算法来解决。以下是创建一个创建编码簿的程序如下。

(初始化步骤) 将码字$c_1, c_2, \cdots, c_k$初始化为从$x_1, \cdots, x_n$中取样的随机数据点。
分区分配步骤）对于每个数据点$x_i$，找到距离最近的码字$\tilde{x_i}$。
- $$\tilde{x_i} = arg min_{\tilde{x_i} \in c_1, \cdots, c_k} l(x_i, \tilde{x_i})$$
更新码表步骤）当$X_j$被设置为所有数据点$x_i$，使$hat{x_i}=c_j$时，根据以下公式更新每个码字$c_j$。
- $$c_j \leftarrow arg min_{c \in \mathbb{R}^d} \sum_{x_i \in X_j} l(x_i, c)$$。
重复步骤2和步骤3，直到达到收敛或达到最大的迭代次数。

在每次迭代中，需要对每个编码进行更新步骤。为了简单起见，这里的解释并不假设矢量分裂，但同样的程序可以用于直接乘积量化。

另外，普通量化技术中使用的距离函数$l$主要是在将数据点$x$量化为$tilde{x}$时，使重建误差最小。

空间部

在矢量量化中，通过设计编码方法可以获得与空间分解相同的效果。例如，我们可以考虑以下Voronoi空间划分以及K-means。

一旦确定了查询向量的相应码字区域，我们的想法是量化并记录与该码字的距离的残差$r_q=q-c_i$。这也提高了效率，因为查询只需要比较同一空间的数据点，而不是整个数据库。

根据不同的尺度，这种机制在涉及到矢量量化时正成为主流。

建议的方法：ScaNN

现在我们来介绍一下所提出的方法。作者通过提出一个新的目标函数--各向异性量化损失函数来记录ANN-Benchmarks的最先进性能，该函数考虑了MIPS精度（检索精度）的提高，这也是最终目标。

我们提到，现有的矢量量化学习将量化过程中的重建误差最小化作为其目标函数。在MIPS的背景下，这似乎是一个中间目标，但实际上，这本身并不是为了忽略MIPS的准确性而设计的。

$$mathbb{E}_q `sum_{i=1}^n (\left< q, x_i `right> - \left< q, tilde{x_i}`right> )^2 = `mathbb{E}_q `sum_{i=1}^n `left< q, x_i - `sum_{i=1}^ntilde{x_i} `right>^2$$。

$$sum_{i=1}^n `mathbb{E}_q `left< q, x_i - tilde{x_i} `right>^2 = `sum_{i=1}^n `mathbb{E}_q (x_i - tilde{x_i}) ^Tqq^T(x_i - tilde{x_i}) =csum_{i=1}^n||x_i - tilde{x_i}||^2$$

因此，量化前后内积值的误差最小化可以被量化误差最小化的问题所取代。由于这些原因，各种研究都侧重于重建误差的最小化。因此，尽管看起来已经设计了一个合适的目标函数此外，对于使用 "MIPS "作为距离函数的情况，作者重点关注以下方面。

对具有较高内积的配对损失给予更大的权重：引入一个以内积为参数的权重函数$w$。
- 强调对提高搜索精度有重大影响的排名靠前的配对
- 上述目标函数考虑了数据点$x$和查询$q$的所有组合。
将量化误差分解为平行和正交方向的各向异性加权故事
- 考虑一下内积的特性

反映上述观点，作者设计的损失函数如下。推导过程和细节被省略，但误差被分为平行和正交方向，并取加权和。

$$l(x_i, \tilde{x_i}, w) = h_{||}(w, ||x_i||) ||r_{||} (x_i, \tilde{x_i})||^2 + h_{\perp}(w, ||x_i||) ||r_{\perp} (x_i, \tilde{x_i})||^2$$

作者还表明，上述权重$w$的设计考虑到了内积，因此平行方向的量化误差比正交方向的量化误差权重更大（省略）。

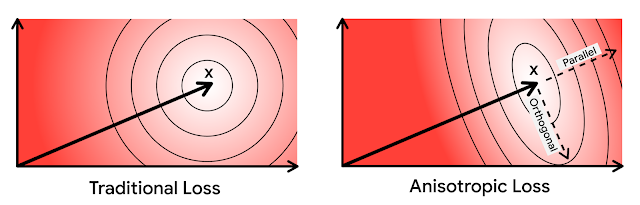
以上是作者提出的各向异性量化损失函数。由于这是对损失函数部分的提议，量化机制本身没有变化，到目前为止已经解释过了，所以作者的方法可以被广泛地应用。

实验

接下来，我们描述了作者进行的几个实验，以表明所提出的量化损失函数可以提高MIPS的性能。

与使用重建误差作为目标函数的方法比较

对量化机制进行了调整，并对传统方法和作者提出的方法进行了比较。数据集是Glove1.2M，它是一个由120万个数据和100个维度的词嵌入组成的集合。

该数据集被量化后，召回率1@10（在检索到的前10个查询中，包含真正的Top1数据点的查询比例）的比较如下图（a）所示，量化前后与Top1数据的内积的相对误差如下图（b）所示。如图所示，如果损失函数的参数$T$合适，我们可以看到所提出的损失函数实现了召回率的显著提高，此外，与顶级配对的相对误差也比较小。

MIPS精度与速度

接下来，我们将MIPS的准确性与其他量化技术（LSQ和QUIPS的三个导数）进行比较。在下图（a）中，我们测量了每个数据点100和200比特的固定比特率的性能，我们可以看到，对于召回率1@N指标中的所有N的范围，作者提出的方法都优于此。

我们还遵循ANN-Benchmarks基准测试协议来测量Glove1.2M的性能，如下图（b）所示。我们可以看到，它明显优于其他竞争方法。

它仍然是一种很好的方法，因为它在通常被认为是准确度和速度之间的权衡的领域中两边都占优势。

摘要

由于MIPS在机器学习的应用中似乎是一个非常重要的技术，不管是CV还是自然语言等领域，我认为这个领域的发展值得关注。就我个人而言，我发现它很有趣，因为它是一个包括实际问题的研究领域，如大规模环境的假设。此外，如果我们将来能在矢量搜索中做一些类似过滤搜索目标（数据库的结构化）的事情，我将非常高兴。我对未来充满了期待。