ファインマン物理学方程式を機械学習で発見する：AI Feynman

Neural Network 2021年08月31日

3つの要点
✔️ 問題を単純で、変数の少ないものに変換する事を繰り返して解く
✔️ ニューラルネットワークによって関数同定問題を改善
✔️ 既存のソフトウェアを上回る予測精度を達成

AI Feynman: a Physics-Inspired Method for Symbolic Regression
written by Silviu-Marian Udrescu (MIT), Max Tegmark (MIT)
(Submitted on 27 May 2019 (v1), last revised 15 Apr 2020 (this version, v2))
Comments: Published on arxiv.
Subjects: Computational Physics (physics.comp-ph); Artificial Intelligence (cs.AI); Machine Learning (cs.LG); High Energy Physics - Theory (hep-th)

code：

本記事で使用している画像は論文中のもの、またはそれを参考に作成したものを使用しております。

はじめに

1601年、ケプラーは火星のデータから軌道を説明する事を試み、40回の失敗の末、軌道が楕円であることを発見しました。これが、特定のデータに一致する記号式を発見する、シンボリック回帰の一例です。

最も単純なシンボリック回帰は、線形結合による線形回帰ですが、一般的なシンボリック回帰問題は未だ未解決のままです。その理由は、関数を記号の文字列としてエンコードすると、それは文字列の長さとともに指数関数的に増加するため、全ての文字列をテストする事は計算量的に困難であるからです。

遺伝的アルゴリズムはこの様に巨大な探索空間での課題解決手法であり、シンボリック回帰問題で成功しているEureqaソフトウェアにも実装されています。

この研究ではニューラルネットワークによってこの最先端技術を更に改善します。ミステリーデータの対称性や分離可能性などの隠れた単純さを発見し、難しい問題をより少ない変数でより単純な問題に再帰的に分割するといった成果を上げました。

アルゴリズム

一般関数 f は非常に複雑であり、シンボリック回帰で発見することはほぼ不可能です。ただし、物理学や他の多くの科学に登場する関数には、多くの場合、次の様に単純化された性質があり、それらを発見しやすくしています。

(1) 単位
関数fとそれが依存する変数には、既知の物理単位があります。これにより次元解析を可能にし、問題を独立変数の少ない単純な問題に変換出来る事があります。

(2) 低次多項式
f（またはその一部）は低次多項式です。これにより、連立方程式を解いて多項式係数を決定し、問題をすばやく解決出来ます。

(3) 単調性
fは、基本関数の小さな構成であり、通常、それぞれが2つ以下の引数を取ります。　これでfを少数のノードタイプを持つ解析ツリーとして表す事が出来ます。

(4) 滑らかさ
fは連続的であり、おそらく分析的です。これはニューラルネットワークを使用してfを近似する事を可能にします。

(5) 対称性
fは、その変数に関して、平行移動、回転、スケーリングの対称性を示します。問題を1つの独立変数が少ない単純な問題に変換出来ます。

(6) 可分性
fは、共通の変数を持たない2つの部分の合計または積として記述出来ます。独立変数を互いに素なセットに分割し、問題を2つの単純なセットに変換できます。

図にアルゴリズムを示します。

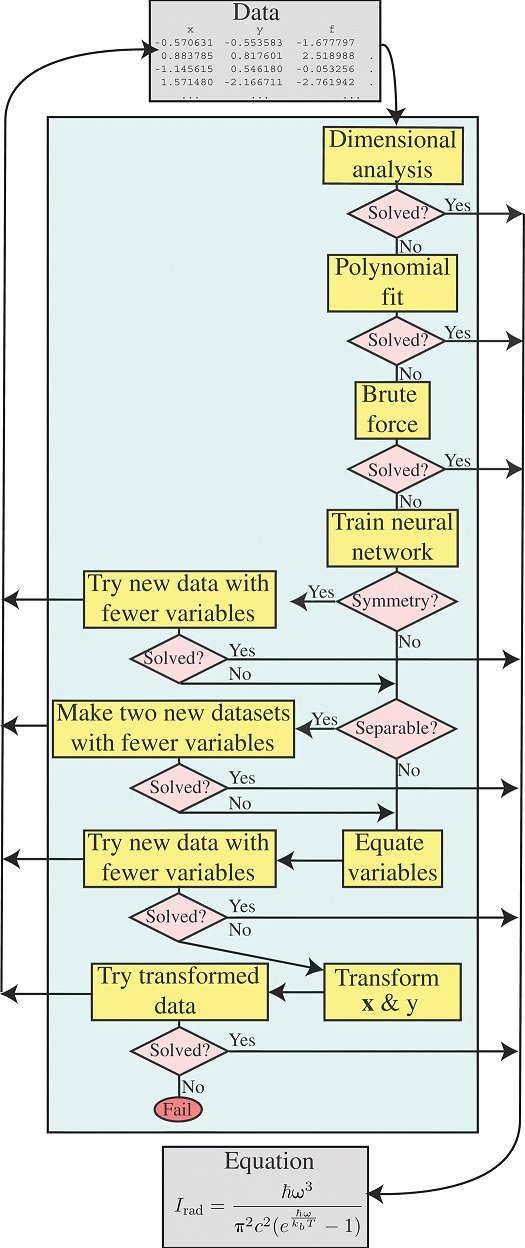
これは人間の科学者がやる様に、順番に一つずつ異なる方略を採り、一度に解決出来ない場合は別々の部分に分割しようとします。

次の図は、9つの変数を持つニュートンの重力の法則がどのように解決されるかの例を示しています。

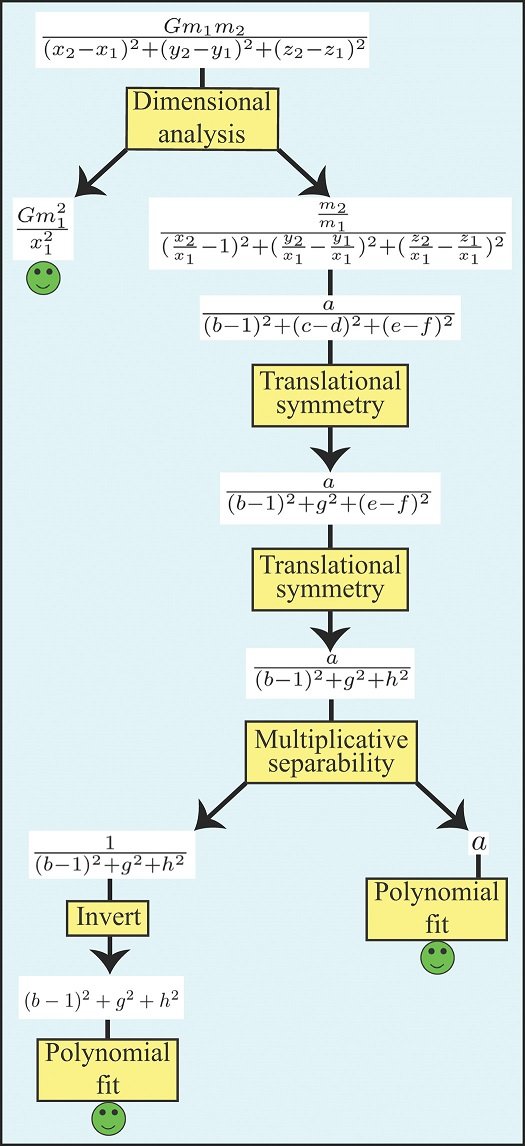
次元解析

次元解析モジュールは、方程式の両辺の単位が一致する前提で、物理学の多くの問題を単純化できるという事実を利用しています。これにより問題が、すべて無次元の変数の数が少ない単純な問題に変換されることがよくあります。

多項式適合

提案手法では、連立一次方程式を解く標準的な方法を使用して、最適な多項式係数を見つけます。

Brute force

Brute forceシンボリック回帰モデルは、原理的には全ての未知関数を解く事が出来ますが、ほとんどの場合、計算量の観点から現実的ではありません。未知データがより単純な部分に変換/分解された後は、通常、Brute force方式が最も役立ちます。

ニューラルネットワークベースのテスト

次元解析を適用した後でも、多くのデータは複雑すぎて、妥当な時間内に多項式適合またはBrute forceで解決する事は出来ません。例えば関数fに平行移動があるかどうかをテストするには、f(x1,x2）= f(x1+a,x2+a)をテストする必要がありますが、通常、データセットはその変数の区間を持たず、従って、テストを実行するにはデータポイント間の正確な高次元補間が必要です。

そのような補間関数を取得するために、入力が与えられた時に出力を予測するようにニューラルネットワークを学習します。

ニューラルネットワークがデータのあるドメイン外で一般化が不十分であるかどうかは気にしないため、これは他の多くのコンテキストよりも簡単な場合があります。このドメイン内で非常に正確である限り、分離可能な関数を正しく因数分解するという目的を果たします。

データベース

本研究およびその他のシンボリック回帰アルゴリズムの定量的テストを可能にするために、6ギガバイトのファインマンシンボリック回帰データベース（FSReD）を作成し、https://space.mit.edu/home/tegmark/aifeynman.htmlから無料でダウンロードできるようにしました。

幅広く物理学分野から方程式をサンプリングするために、データベースは、独創的なファインマン物理学講義から100の方程式を使用して生成しました。これに加えて、他の独創的な物理学の本から、より挑戦的な20の方程式を取得しています。こちらを、Bonus mysteriesとします。

結果比較

AIファインマンとEureqaアルゴリズムの両方を、ファインマンデータベースに適用してシンボリック回帰を行い、データ毎に最大2時間のCPU時間を利用して比較しました。その結果Eureqaが71％を解いたのに対し、AIファインマンは100％を解決しました。

結果を詳しく調べると、Eureqaには解けなかった問題は、最も複雑なデータに対するものであることがわかります。

ニューラルネットワークでは、対称性と分離可能性を発見することで変数を排除出来るため、次元解析モジュールなしでAIファインマンを再実行すると、ニューラルネットワークはさらに重要になります。ニューラルネットワークは分離可能性と対称性を発見してファインマン方程式の93％を解きます。

AIファインマンは処理の進行と共に、独立変数の数を繰り返し減らしており、正しい方向へ進んでいる事が事実上保証されています。対してEureqaなどの遺伝的アルゴリズムは、より良い近似を連続して見つけることによって進歩しますが、より正確な記号表現が真実に近いという保証はありません。

Eureqaが全く異なる関数形式でかなり近似であるが不正確な式を見つけた場合、その局所解に陥ってしまうリスクがあります。これは、遺伝的アプローチの基本的な課題を反映しています。

データサイズの影響

データセットのサイズを変更した場合の影響を調査するために、AIファインマンが失敗するまで、各データセットのサイズを10分の1に繰り返し縮小しました。ほとんどの方程式は、10個のデータポイントのみを使用した場合でも、多項式適合とBrute forceによって検出されます。

真の方程式が複雑な場合、アルゴリズムが過剰適合し、誤った方程式を「発見」する可能性があるため、場合によっては100個のデータポイントが必要になります。

ニューラルネットワークを使用して解く必要がある方程式では、ネットワークが未知関数を十分に正確に学習出来るよう、かなり多くのデータポイント（100～1000000）が必要です。

ノイズの影響

ほとんどの場合実際のデータは、測定誤差やその他のノイズがあるため、正規乱数をその従属変数yに追加しました。

ノイズレベル 0.000001 からAIファインマンが失敗するまでノイズレベルを増加させます。ほとんどの方程式は0.0001以下の値で正確に復元できますが、半分は0.01でも解かれます。

Bonus mysteries

先の100方程式は、AIファインマンアルゴリズムのパフォーマンスを最適化するために実装とハイパーパラメータを改善したため、トレーニングセットと見なす必要があります。それに対して20のBonus mysteriesは、AIファインマンアルゴリズムとそのハイパーパラメーターを設定した後で分析したため、テストセットと見なす事が出来ます。EureqaがBonus mysteriesの15％しか解けなかったのに対し、AIファインマンは90％を解決しています。

ボーナスミステリーで成功率が大きく異なるという事実は、方程式の複雑さが増していることを反映しており、ニューラルネットワークベースの戦略が必要になります。