活性化関数まとめ
3つの要点
✔️ 活性化関数に関するサーベイ論文
✔️ 様々な活性化関数を分類ごとに紹介
✔️ 画像分類・言語翻訳・音声認識における活性化関数の比較実験結果の紹介
A Comprehensive Survey and Performance Analysis of Activation Functions in Deep Learning
written by Shiv Ram Dubey, Satish Kumar Singh, Bidyut Baran Chaudhuri
(Submitted on 29 Sep 2021)
Comments: Submitted to Springer.
Subjects: Machine Learning (cs.LG); Neural and Evolutionary Computing (cs.NE)
code:

本記事で使用している画像は論文中のもの、紹介スライドのもの、またはそれを参考に作成したものを使用しております。
はじめに
深層学習にて用いられる活性化関数として、sigmoidやtanhやReLUをはじめとした様々な関数が提案されています。
本記事では、これまでに提案された活性化関数について、その分類・特性・性能比較などの重要な情報を詳細にまとめたサーベイ論文について紹介します。深層学習における活性化関数の選択や、新たな活性化関数の設計などに、これらの内容が役立てば幸いです。
活性化関数について
はじめに、活性化関数はその特徴・特性から、以下のように分類することができます。

図のCharacteristics Typeは、それぞれの活性化関数が元とする関数を示しています。具体的には、Sigmoid/Tanhベース、ReLUベース、指数ユニットベース、学習・適応型、その他に分類されます。
これらの分類の中で、特に主要な活性化関数の特徴は以下の通りです。
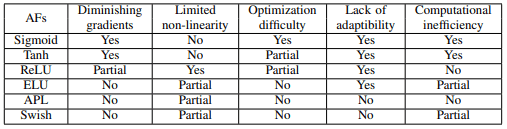
Properties of AFsは、それぞれの活性化関数の定義に関する特性を示しています。具体的には、パラメトリックか否か、単調(Monotonic)か否か、滑らかな(Smooth)関数か否か、有界(Bounded)であるか否か、出力の範囲などの特性によって分類することができます。
Different Applicationsは、それぞれの活性化関数がどのようなタスクのために用いられるかを示しています。
以下のセクションでは、Characteristics Typeの分類に基づいて様々な活性化関数について解説します。
Sigmoid/Tanhベースの活性化関数
初期のニューラルネットワークでは、活性化関数として(Logistic) SigmoidやTanhが主に用いられていました。これらは以下の図(紫・緑線)・数式で表されます。
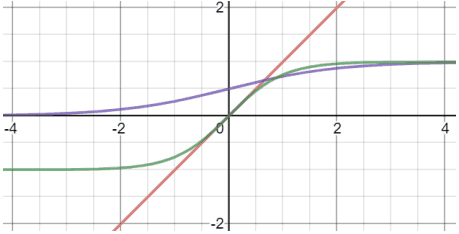
$Sigmoid(x)=1/(1+e^{-x})$
$Tanh(x)=(e^x-e^{-x})/(e^x+e^{-x})$
Sigmoid・Tanh関数はどちらも、勾配消失や計算が複雑であるなどの課題を抱えています。これらの関数をベースにした活性化関数は以下の表にまとめられます。
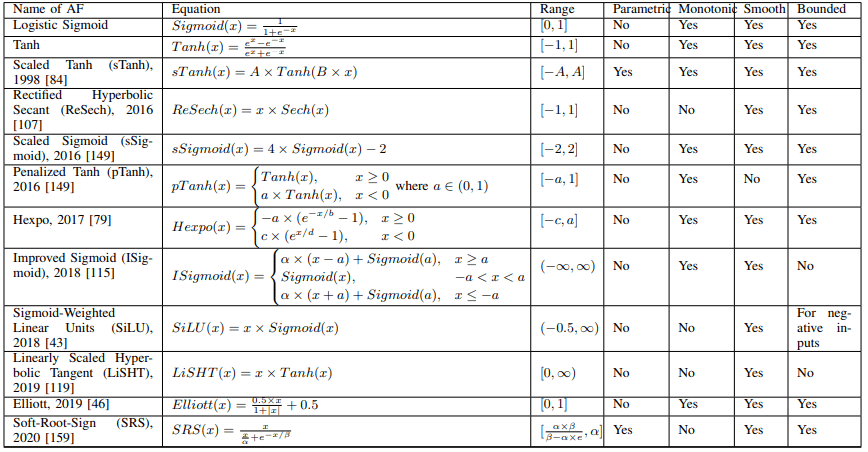
例えばScaled Sigmoid(sSigmoid)では、適切なスケーリングを行うことでSigmoidの性能を向上させています。
またPenalized Tanh(pTanh)では、Tanhの負の領域にペナルティをかけることで原点付近の傾きが一様であることを解消し、自然言語処理タスクで良好な性能を発揮することが示されました。
表では示されていない事例として、勾配消失に対処するためにノイズを利用する()ことも提案されています。
総じて、追加のパラメータを用いてスケーリングを行ったり、勾配の特性を変化させることで、勾配消失問題の緩和や性能向上を目指しています。
ReLUベースの活性化関数
ReLU関数は$Relu(x)=max(0,x)$で表される非常にシンプルな活性化関数です。この関数はSigmoidやTanhと比べ、計算が単純であり、勾配消失問題が起きにくい等の利点により、深層学習にて非常によく用いられています。
ReLUを改善した活性化関数は、ReLUのもつ特性のうち、負の値が利用されない、非線形性が限定されている、出力が非有界である、などの点に対処しています。ReLUベースの活性化関数は以下の表の通りです。

・ReLUの負の値の非活用について
はじめに、ReLUが負の値を利用しない点に対処した事例について紹介します。
代表的なものはLeaky ReLU(LReLU)で、これは負の領域を傾きの小さい線形関数($x<0$のとき$LReLU(x)=0.01x$など)としてReLUを拡張しています。LReLUは様々な場面で用いられ、優れた性能を示していますが、LReLUの傾きをどのように設定すべきかを見つけることは困難です。
そのため、負の領域の傾きを学習可能パラメータにしたParametric ReLU(PReLU)、傾きを一様分布からランダムにサンプリングするRandomized ReLU(RReLU)などの派生も提案されています。
また、Parametric Tanh Hyperbolic Linear Unit(PTELU)では、負の領域について学習可能パラメータを持つTanhを利用することも提案されています。
別の方向性として、Concatnated ReLU(CReLU)では、ReLU(x)とReLU(-x)の二つの出力を結合することで負の値の情報を利用しています。
また、Flexible ReLU(FReLU)、Randomly Translational ReLU(RTReLU)、Average Biased ReLU(ABReLU)では、学習可能パラメータまたはランダムな数値または特徴量の平均値をもとに、ReLUをx軸またはy軸方向に平行移動させることで、負の値を利用しています。
・ReLUの限定的な非線形性について
次に、ReLUの非線形性を拡張する方向での改善例について紹介します。
S-shaped ReLU(SReLU)では、三つの線形関数と四つの学習可能パラメータを用いて、ReLUの非線形性を高めています。同様に、Multi-bin Trainable Linear Units(MTLU)も、多数の線形関数を組み合わせています。
また、Elastic ReLU(EReLU)では、正の領域の傾きをランダムに設定することで非線形性を制御します。
別の方向性として、ReLUとTanhを組み合わせたRectified Linear Tanh(RelTanh)や、対数関数とReLUを組み合わせたNatural-Logarithm ReLU(NLReLU)など、ReLUと他の関数を組み合わせる場合も存在します。
・ReLUの非有界な出力について
ReLUやその亜種の関数は、出力が非有界であることに伴い、学習が不安定になることがあります。
この点への対処として、Bounded ReLU(BReLU)では、出力の上限を設定することで、学習の安定性を高めています。
指数ユニットベースの活性化関数
指数関数を用いる活性化関数は、SigmoidやTanh、ReLUが抱える問題に対処するために提案されました。これに分類される活性化関数のうち、代表的なものであるELUは以下の式で定義されます。

ELUはReLUの利点を兼ね備えつつ、Leaky ReLUやParametric ReLUと比べ、負の領域についてノイズに対するロバスト性を高めています。
このELUをベースにした活性化関数として、例えばELUのスケーリングを行うScaled ELU(SELU)や、$\alpha \neq 1$についても連続微分可能にしたContinuously Differentiable ELU(CELU)、活性化マップの平均値をゼロに近づけるParametric Deformable ELU(PDELU)などが提案されています。
ReLUの場合と同様、正の入力に対する関数を修正して有界にする場合も存在します。
学習・適応型活性化関数
次に、学習可能なパラメータを持つ活性化関数について紹介します。代表的なものはSwishなどで、これらは以下の表にまとめられます。

例えばSwishでは、学習可能パラメータである$\beta$に応じて、活性化関数の形状を線形関数からReLUの間で調整します($\betaが小さければ線形に、大きければReLUに近づきます$)。
Swishの拡張例としては、ESwishやflatten-T Swish、Adaptive Richard's Curve weighted Activation(ARiA)などが存在します。
他にも、こちらの研究や、PReLUとPELUを組み合わせたAdaptive AF(AAF)のように、複数の活性化関数を学習可能パラメータにより組み合わせる事例も存在します。
総じて、学習可能パラメータにより非線形関数の形状を制御したり、複数の活性化関数を組み合わせることにより、データセットやネットワークに合わせた適切な活性化関数を実現することを目標としています。
その他の活性化関数
最後に、上述したもの以外にあたる活性化関数について紹介します。
・Softplus活性化関数
Softplusは$log(e^x+1)$で定義される関数です。
これをベースにした活性化関数として、例えばSoftplus Linear Unitでは、SoftplusとReLUを組み合わせています($x \geq$ 0のとき$\alpha × x,x<0$のとき$\beta × log(e^x+1)$)。
他にもRectigied Softplus(ReSP)やRand Softplusなどでも、Softplus関数が利用されています。
また、$Mish(x)=x×Tanh(Softplus(x))$で定義されるMish活性化関数なども提案されており、これは物体検出のためのYOLOv4モデルで利用されています。
・確率的活性化関数
確率的活性化関数として、RReLU、EReLU、RTReLU、GELUなどが存在します。
例えばGaussian Error Linear Unit (GELU)は、$x\Phi(x)$(ただし、$\Phi(x) = P(X ≤ x), X ~ N (0, 1)$)で定義される関数となります(これは$xSigmoid(1.702x)$として近似できます)。
他にも、GELUの拡張例であるSymmetrical Gaussian Error Linear Unit(SGELU)や、Doubly truncated Gaussian distributions、Probabilistic AF (ProbAct)なども提案されています。
・多項式活性化関数
多項式を利用する活性化関数としては、Smooth Adaptive AF (SAAF)、ReLUを拡張したRectified Power Unit (RePU)($x \geq 0 についてx^s(sはハイパーパラメータ)$)、Pade Activation Unit (PAU)、Rational AF (RAF)などが存在します。
・サブネットワークによる活性化関数
Variable AF(VAF)では、ReLUによる小規模なサブニューラルネットワーク自体を活性化関数として利用します。
これに類似する手法として、Dynamic ReLU(DY-ReLU)やWide Hidden Expansion(WHE)、AF Unit(AFU)などが存在します。
・カーネル活性化関数
活性化関数をカーネル関数で展開する例として、Kernel-based non-parametric AF (KAF)やその拡張例であるmultikernel AFs (multi-KAF)が存在します。
SOTAの活性化関数について
様々なデータセットやモデルに対するSOTAの活性化関数は以下の表のようになります。
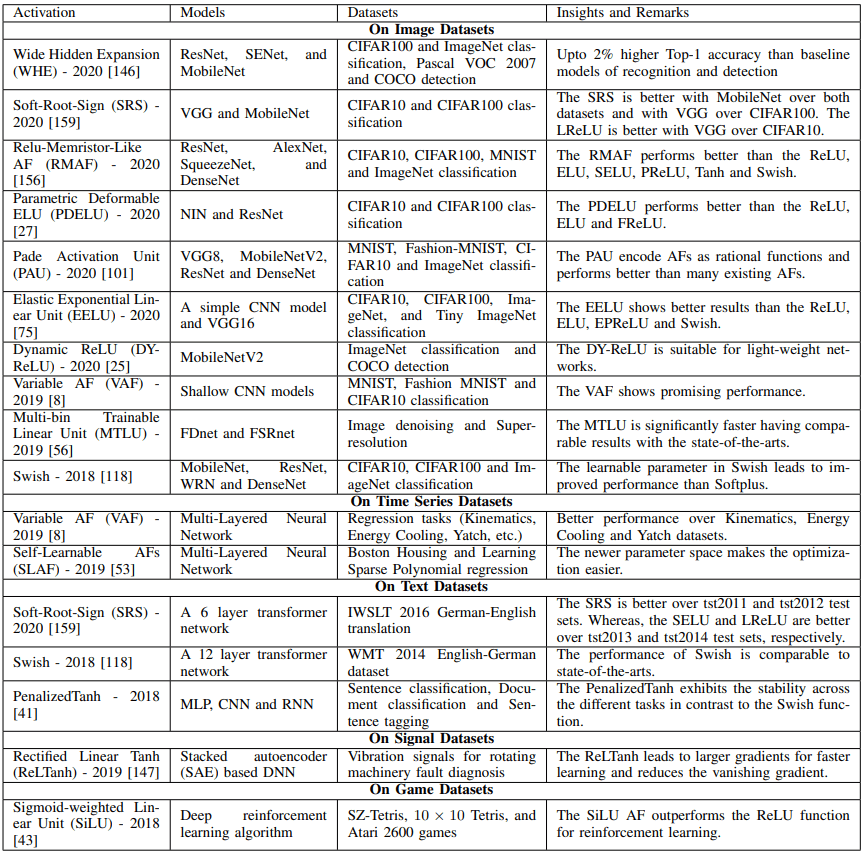
どのようなデータセットやモデルに対し、どの活性化関数が優れた結果を示しているのかについては、上記の表が参考になるでしょう。また、既存の活性化関数についてのサーベイ論文一覧は以下の通りです。
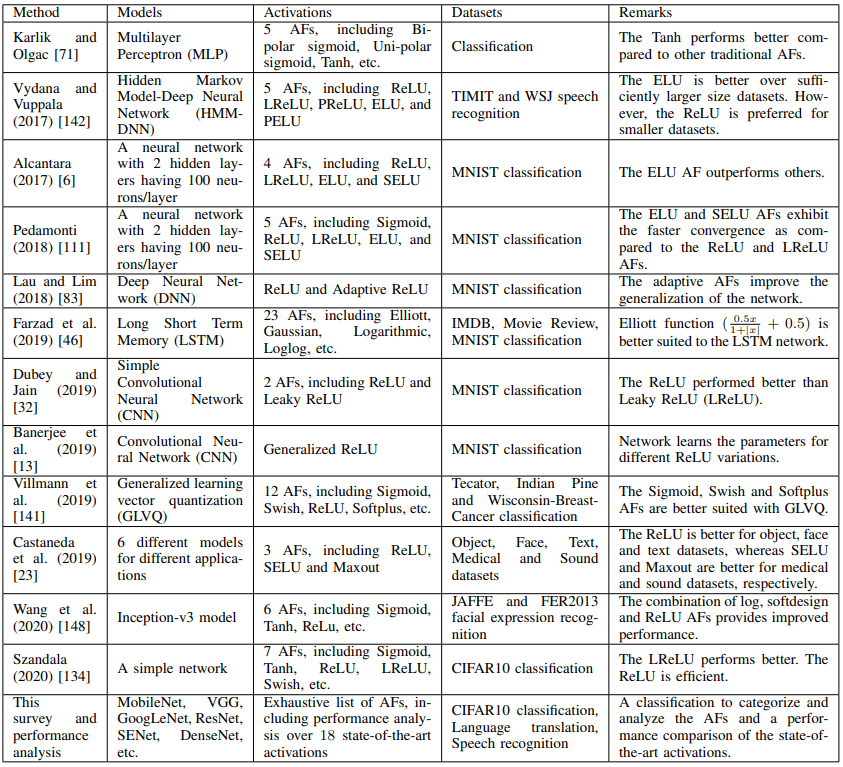
実験結果
元論文では、画像分類(CIFAR10/100)・言語翻訳(ドイツ語→英語)・音声認識(LibriSpeech)の三つのタスクについて、18種類の活性化関数を用いて実験を行っています。実験に用いられた活性化関数は以下の通りです。
- Logistic Sigmoid
- Tanh
- Elliott
- ReLU
- LReLU
- PReLU
- ELU
- SELU
- GELU
- CELU
- Softplus
- Swish
- ABReLU
- LiSHT
- Soft-RootSign (SRS)
- Mish
- PAU
- PDELU
はじめに、CIFAR10における実験結果は以下の通りです。

次に、CIFAR100における実験結果は以下の通りです。
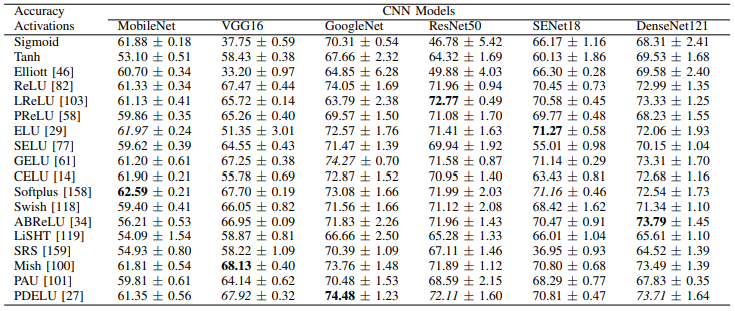
総じて、各モデルごとに最適な損失関数が異なることがわかります(例えばSoftplus、ELU、CELUはMobileNetで優れた性能を示しています)。また、CIFAR100における各活性化関数の学習時間(100エポック)は以下の通りです。
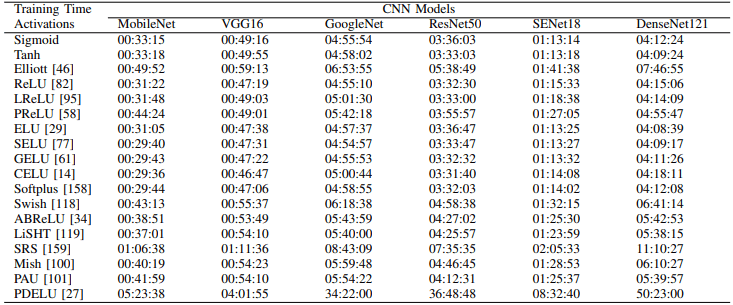
PDELU、SRS、Elliottなどが特に時間がかかることがわかります。さらに、各モデルのCIFAR100における学習曲線は以下の通りです。
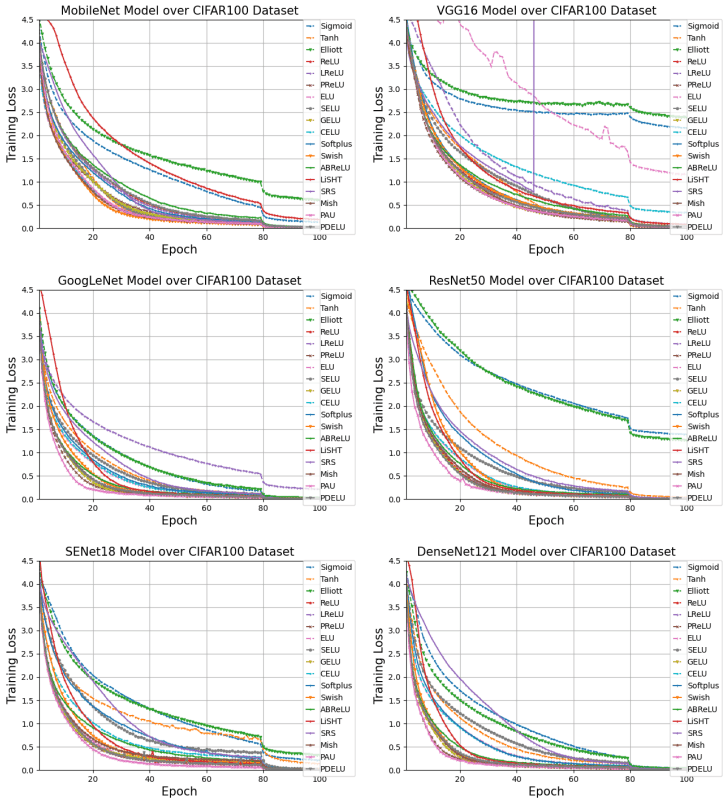
PAU、PReLU、GELU、PDELUなどが特に高速に収束しています。最後に、翻訳・音声認識タスクにおける結果は以下のようになります。

言語翻訳ではTanh、SELU、PReLU、LiSHT、SRS、PAUが、音声認識ではPReLU、GELU、Swish、Mish、PAUなどが優れた結果を示しています。
まとめ
本記事では、様々な活性化関数について、その分類・特性・性能比較などの重要な情報をまとめたサーベイ論文について紹介しました。
各データセットやモデルについての活性化関数の比較実験なども含め、非常に多くの情報が含まれており、活性化関数について詳しい情報を得たい場合には非常に有用な論文ですので、一度元論文に目を通してみることをおすすめします。
この記事に関するカテゴリー