Increase Affine Accuracy First! Registration Using ViT: C2FViT

3 main points
✔️ Proposed C2FViT for Coarse-to-Fine positioning with convolution and MHSA
✔️ Quantitative analysis of the performance of affine registration alone, which has been neglected by existing methods
✔️ Better performance and generalization performance than CNN-based methods and comparable accuracy to non-training-based methods

Affine Medical Image Registration with Coarse-to-Fine Vision Transformer
written by Tony C. W. Mok, Albert C. S. Chung
(Submitted on 29 Mar 2022 (v1), last revised 30 Mar 2022 (this version, v2))
Comments: Accepted by CVPR2022.
Subjects: Computer Vision and Pattern Recognition (cs. CV)

code:.

The images used in this article are from the paper, the introductory slides, or were created based on them.

Introduction

We present Coarse-to-Fine Vision Transformer (C2FViT), a state-of-the-art method for affine registration that combines the advantages of ViT and convolution to perform global and local alignment with high accuracy, and then performs them Coarse-to-Fine at multiple resolutions. The proposed method outperforms existing learning-based methods on brain MRI data by combining the advantages of ViT and convolution to perform global and local alignments accurately, and by performing these alignments in a Coarse-to-Fine manner at multiple resolutions. While the performance of the proposed method is important, it is also important to note that the performance of affine registration alone, which has been neglected, was also evaluated using existing methods. We feel that this paper is essential for understanding the trends in affine registration.

Major contributions include

• Quantitative analysis of the accuracy, robustness, and generalization performance of existing affine registration methods in 3D brain MRI images.
• Proposed C2FViT, which performs Coarse-to-Fine (rough to fine) alignment in convolutional ViT.
• Generalized by decomposing the affine matrix into translation, rotation, scale, and shear parameters
• Excellent performance and generality in two experiments of standardized and atlas-based registration to the MNI152 template

Let's take a quick look at C2FViT.

affine registration

This paper focuses on affine registration. Registration is the task of aligning between two images. By figuring out where one region of an image corresponds to in another image, it has a wide range of applications in medicine, such as monitoring the progress of the same patient or comparing symptoms between different patients. The goal of the model is to learn a displacement field A that deforms a certain image moving to match a fixed. Below is an example of the data set and model registration used in this paper.

The deformations handled by displacement fields can be broadly classified into affine and nonlinear deformations. There are two approaches, depending on how they are handled. The table below gives an overview and disadvantages of each.

Unless affine deformations are captured, the performance of positioning is greatly degraded. Most existing methods consist of a two-stage process that first performs global alignment by affine registration, including translation, rotation, and scale, and then applies Deformable Registration to remove fine nonlinear deformations. In this approach, affine transformations in the first stage are often optimized individually without learning, such as convex optimization or adaptive gradient descent, which has the drawback that the processing time is enormous.

On the other hand, there are recent methods that learn and process affine and nonlinear transformations in a single step in a CNN, without distinguishing between them. While this approach is fast, affine deformations must also be captured by CNN. In general, affine deformations between images are often global, so a CNN approach that can only capture local changes in the kernel is not appropriate. Experiments have shown that existing CNN-based methods perform poorly on unknown images with large misalignments.

Coarse-to-Fine Vision Transformer (C2FViT)

For the above reasons, this paper focuses on affine registration in the first stage and proposes C2FViT, a new affine registration model that departs from the existing CNN-based approach and utilizes the Vision Transformer (C2FViT), a new affine registration model that uses the Vision Transformer. It also introduces a convolutional layer to introduce a moderate inductive bias and is a Coarse-to-Fine estimation model that uses multiple resolutions to estimate local variation in turn from global variation.

Affine matrix decomposition

C2FViT estimates the four types of parameter matrices of an affine matrix independently. The affine transformation is represented by the following equation This equation can be used to translate, rotate, scale, and shear the image. (x,y) is the position of each pixel in the image to be applied and (x',y') are the coordinates after an affine transformation. The purpose of affine registration is to estimate the parameters of this matrix.

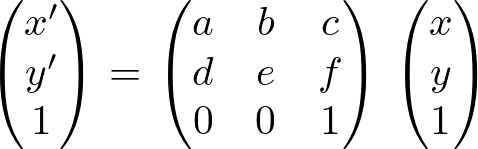
Existing methods often estimate the above equation, but the above equation is less versatile because it is an equation that performs four different types of transformations at once. Since affine transformations allow each of the four different transformations to be performed independently, it is better to be able to estimate translations, scaling, rotations, and shears independently to increase the range of registration. For example, a rigid-body registration can be performed by excluding the scaling and shear matrices from the four transformations. Therefore, C2FViTestimates the translation, scaling, rotation, and shear parameters independently.

Compatibility of Attention and Folding

Figure (c) in the next figure shows an overview of the proposed method, while (a) and (b) are existing CNN-based approaches. Concatenation-based approach (a) uses the same network for both moving and fixed, but it is not suitable for affine registration because it cannot capture dependencies larger than the kernel size. In (b), separate networks are prepared for fixed and moving. Since the features are integrated through the Global Average Pooling at the end of each network, global estimation is possible to some extent, but on the other hand, local relationships are neglected.

On the other hand, the proposed method, C2FViT, processes image pairs simultaneously, but captures global relationships in the MHSA layer and local features in the convolution layer at the same time. The changes are in the patch embedding and Feed-Forward layers. While ordinary ViT transforms local patches in the input image into Q, K, and V by linear projection, C2FViT obtains patch embedding by the 3D convolution layer to emphasize local features as well. In addition, while the usual ViT passes each patch through the Feed-Forward layer independently, C2FViT places the output of the MHSA layer back into the 3D space and applies 3D Depth-Wise convolution to further strengthen the locality of the model. In the figure, this is denoted as Convolutional Feed-Forward.

The proposed method builds this Convolutional Patch Embedding and N Transformer Encoder processes as a single stage.

Multi-Resolution strategy

C2FViT takes a step-by-step approach to remove affine deformations at multiple resolutions. First, image pyramids Mi, Fi are created for the moving, fixed set M, F downsampled at various scales, where i ranges from 1~L and Mi, Fi is downsampled at a scale of 0.5^(L-i). In other words, a smaller i results in a lower-resolution, global registration, while i=L results in a higher-resolution registration at the original image size.

The proposed method performs L(=3) stages of stepwise alignment, with one stage for each resolution. At first, the lowest resolutions F1 and M1 are aligned. The displacement field A1 obtained at this time is reflected in M2 of the next resolution by Spatial Transform, and further alignment is performed. In addition, the features of the previous resolution are added to the next Convolutional Patch Embedding, enabling Coarse-to-Fine registration that takes into account the features and alignments of the previous low resolutions.

unsupervised loss

The loss of alignment is obtained by evaluating whether the actual moving-transformed image matches FIXED with the estimated parameters. In this model, the negative value of NCC, a similarity measure commonly used in registration, is calculated at each resolution i and summed; the index w of NCC is the local window and Mi(Φ) is the image after alignment.

semi-teachable loss

The previously introduced DIR model VoxelMorph can be trained semi-supervised when fixed and moving have segmentation masks with typical geometric structures, and this model can be trained in the same way. This is because the registration can be evaluated more directly by evaluating the overlap of the segmentation masks after alignment. The model can be extended to semi-supervised learning by adding the following Lsig to the unsupervised loss Lsim The loss is calculated as the negative value of the overlap of the segmentation masks SFi and SMi at each resolution, where K is the number of segmentation masks. The weight λ = 0.5 is assumed.

Advanced Settings

The number of output channels d of Convolutional Patch Embedding is fixed at 256 and the map size is fixed at 4096 dimensions with flattens. It seems that the stride and padding kernel sizes are determined relative to the input map size to always maintain a constant dimensional embedding. Also, although Layer Normalization is used in regular ViT, it did not work in this method and task, so it was removed.

experiment

Experiments validate the performance of the proposed method on a standardized 3D brain MRI image task and an atlas-based affine registration task to verify the superiority of the proposed method.

Task Overview

Standardization to MNI152

MNI152 is a template for brain imaging. It standardizes the brain of each subject to match a standard brain (template) to integrate various studies on the brain. This allows for a unified coordinate system and scale, and anatomical mapping. Since, strangely, the brains of all humans are merged into one brain, an improvement was made to use the average of the brains of several people who have undergone standardization as the template. This process was performed and improved several times, and finally, 152 brains were standardized to create the average brain, which is MNI152. In this paper, we register the OASIS dataset to MNI152 and validate the performance of a typical registration task.

Atlas-based registration

This task involves registration to each image in the dataset itself, rather than to the mean brain. In training, we select a randomly selected pair on the OASIS dataset. At test time, we let the model register on the OASIS dataset and an unknown LPBA dataset. The goal is to validate the performance of the model and generalization performance by applying it to the same and unknown datasets; three from OASIS and two from LPBA are randomly selected as atlases, and the test data from each dataset is registered to the atlases.

data-set

OASIS Data Set

This dataset is 414 T1-weighted brain MRI images. In this paper, FreeSurfer is used to perform preprocessing such as resampling and padding, and the data is divided by Train:Valid: Test=255:10:149.

LPBA Data Set

This data set consists of 40 brain MRI images. All are used as test data in this paper.

baseline

All models are optimized with 3 resolutions. L=3 in the proposed method.

Non-learning based

Traditional non-training-based registration uses ANTs and Elastix as SoTA models; both are optimized with adaptive gradient descent using mutual information content.

Learning-based

The two existing methods are ConvNet-Affine and VTN-Affine. Each of them builds only affine networks based on the paper. All learning-based methods are extended to semi-supervised and denoted ConvNet-Affine-semi, VTNAffine-semi, and C2FViT-semi, respectively.

evaluation

Four evaluations are performed: Dice similarity coefficient (DSC), 30% lowest DSC of all cases (DSC30), and 95% percentile of Hausdorff distance (HD95), which is a measure of the accuracy of registration. The fourth is the Test, which is a measure of execution time that differs significantly between the unlearning and learning bases. The standardization evaluates masks for four subcortical structures: caudate nucleus, cerebellum, putamen, and thalamus; OASISevaluates23 subcortical structures; and LPBAevaluates all manual segmentations, including cerebrospinal fluid (CSF), gray matter (GM), and white matter (WM).

For training-based models, we also compare the accuracy with and without center of mass (CoM) initialization. This is because CoM initialization is often used in affine registration after aligning the center of mass of the input images.

Accuracy and Robustness

First are the results without CoM initialization. It can be seen that the Dice score is low for all data tasks in the pre-positioning state, indicating a large misalignment. The proposed method outperforms ConvNet-Affine and VTN-Affine in DSC, DSC30, and HD95 in all three tasks, indicating that it is robust and accurate in affine registration with large misalignment. Conversely, the affine subnetworks of existing methods were found to be inadequate for large misalignment.

Next is the accuracy with CoM initialization. Aligning the center of gravity improves the Dice scores from 0.14, 0.18, and 0.33 to 0.49, 0.45, and 0.45, respectively, indicating that the alignment is roughly achieved only by translating. All of the learning-based methods have significantly improved accuracy with CoM initialization, especially the proposed method achieves the same accuracy as ANTs and Elastix for the unsupervised model C2FViT, and the semi-supervised model C2FViT-semi has been standardized to MNI152 and OASIS's The highest accuracy was achieved with atlas-based registration.

generalization performance

The accuracy of the LPBA dataset differs from that of the other two tasks. The existing ConvNet-Affine and VTN-Affine methods are not able to align at all, with or without CoM, or with the -semi-extension, with the Dice score remaining almost unchanged from the initial value. On the other hand, C2FViT is slightly less accurate than Elastix but is almost as accurate. The results show that C2FViT has a strong generalization performance compared to existing methods.

The results show a significant advantage in terms of execution time, accuracy, and generalization performance when compared to ANTs and Elastix, which have huge execution times, and less robust training bases.

Affine matrix decomposition

Accuracy comparisons are also made between the proposed method's direct estimation of the affine matrix and the decouple estimation decomposed into translation, rotation, scaling, and shear as described above. As shown in the table, the decentralized estimation is more accurate and general in that it can be easily applied to other parametric registrations.

summary

In this presentation, we introduced Coarse-to-Fine VisionTransformer (C2FViT) for affine registration of 3D medical images, which, unlike previous studies using CNN-based affine registration, emphasizes global feature extraction by Self-Attention. Unlike previous studies that used CNN-based affine registration, we focused on global feature extraction using Self-Attention. By combining moderate locality through convolution with coarse-to-fine alignment, C2FViT achieves better registration accuracy than CNN-based methods. The difference between C2FViT and existing methods is particularly large under data with large misalignments, and it also shows robustness to unknown data sets. The semi-supervised C2FViT-semi outperforms non-training-based methods by utilizing dataset-specific information, showing superiority in accuracy, robustness, run time, and generalization performance.

As a challenge, it raises the accuracy gap between unsupervised learning-based methods and traditional non-training-based methods. The report states that task-specific data expansion could lead to improved accuracy. We look forward to future developments.

Categories related to this article

• Image Recognition
• Machine Learning
• Deep Learning
• Medical Care
• Medical
• Transformer
• CVPR