A Deep Learning Implementation Of The Independent Mechanism Hypothesis Of Causality.

Neural Network 06/08/2021

3 main points
✔️ Propose RIMs with an "independent mechanism" in which only relevant parts of the environment respond to changes in the environment
✔️ Incorporate a mechanism to induce competition by combining Attention and LSTM
✔️ Verified the improvement of generalization performance by RIMs through extensive experiments

Recurrent Independent Mechanisms
written by Anirudh Goyal, Alex Lamb, Jordan Hoffmann, Shagun Sodhani, Sergey Levine, Yoshua Bengio, Bernhard Schölkopf
(Submitted on 24 Sep 2019 (v1), last revised 17 Nov 2020 (this version, v6))
Comments: Published on arxiv.
Subjects: Machine Learning (cs.LG); Artificial Intelligence (cs.AI); Machine Learning (stat.ML)

code：

The images used in this article are either from the paper or created based on it.

Introduction: independent structures that exist in the world

Physical processes can be thought of as being produced by a combination of subsystems with a simple modular structure. For example, two balls can be modeled as almost independent mechanisms, except that they are interlocked by gravity but occasionally collide and interact strongly with each other.

The proposed method in the introductory paper, named Recurrent Independent Mechanisms (RIMs), tries to realize a modular structure with independent mechanisms that humans use to recognize the natural world using a deep learning approach.

In designing RIMs, it is important for the mechanisms to be independent and to communicate sparsely. Independence between modules is a prerequisite for being able to interfere locally in causal inference and is considered a very important property. On the other hand, sparse communication between modules is to avoid dense exchange, which leads to independence where only modules relevant to the input respond. Specifically, we will discuss in detail how the architecture of RIMs should be designed, and from which angles the generalization performance of RIMs can be evaluated.

Proposed method: Recurrent Independent Mechanisms (RIMs)

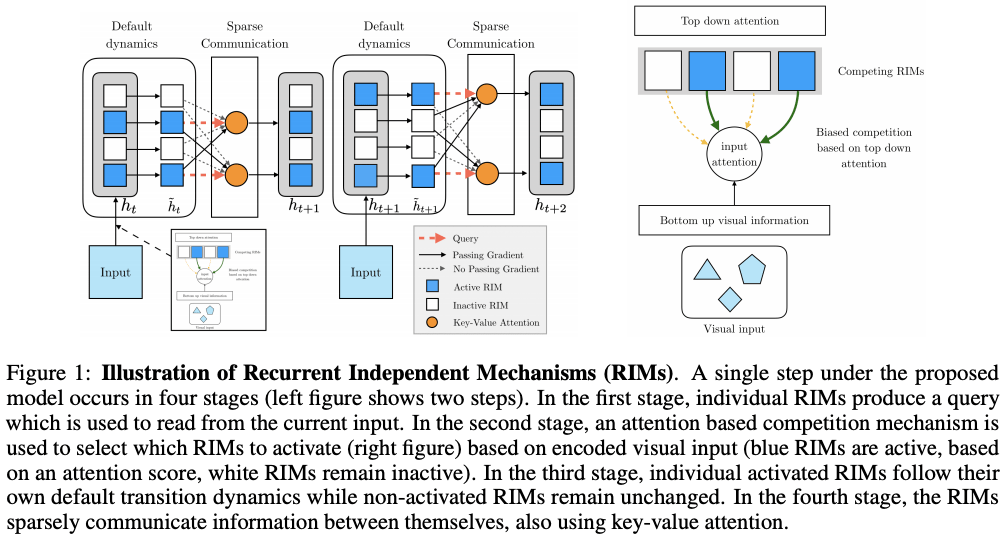
After an overview of RIMs and architectural design, the details of RIMs will be described in detail in four steps.

The individual subsystems, which divide the overall model into k parts, are designed to capture the changes in the observed series information in an iterative manner. These subsystems are called Recurrent Independent Mechanisms (RIMs), and each RIM learns from the data to have a different function.

# The kth RIM has a value vector h_(t,k) and a parameter θ_k at time t. However, t=1,... ,t.

Figure 1 shows an overall view of the RIMs. The authors designed the RIMs so that each RIM is differentiated and has its own dynamics, but occasionally interacts with other RIMs or embeddings of selected inputs. In particular, by using Attention Mechanisms, RIMs can manipulate only a few key/value variables, keeping the total number of parameters small. This differentiation and modularity not only provide computational and statistical benefits but also prevent individual RIMs from dominating the computation and encourages the decomposition of the computation into simple elements that can be easily recombined and reused.

We expect that the RIMs architecture will allow us to learn more robust systems than learning one large homogeneous system. This requires various properties of RIMs, such as that they should maintain their own functionality even when other RIMs change, which are detailed in Appendix A of the paper.

Key/value attention mechanism to handle independent variables

Each RIM should be excited and updated only when it receives input relevant to itself in the first stage of receiving input. At each time, each of the k RIMs computes its relevance to the input using the Attention mechanism and competes for resources. If the hypothesis introduced in the Introduction that the data is governed by independent physical phenomena is correct, then the RIMs are said to be able to learn the independent mechanism naturally (Parascandolo et al. 2018).

We use Soft-Attention, which is effective in many fields, to generate Query (Q) from RIMs, Key (K), and Value (V) from input information and the degree to which each RIM is related to the input information can be calculated by Soft-Attention below.

# When the input and output of each RIMs are multiple objects, the RIMs can dynamically select the objects to be input through Soft-Attention calculation to the Key(K) and Value(V) of the input using its own Query(Q).

Select RIMs activation in Top-Down format

The proposed method learns to dynamically select RIMs that are related to the input by the fact that the RIMs to be activated are determined by the result of the interaction between the RIMs and the input at the current time. At each time, we choose the top k RIMs of the Score obtained by the Attention mechanism described in Section 2.1. That is, at each time, only the k RIMs with a higher Attention Score than the other RIMs can be read from the input, and only the selected RIMs can be updated.

The process of selecting the RIMs to be activated in the Top-Down form to access the input from these RIMs is shown on the right of Figure 1. As shown in Equation (2), the Key and Value in the Soft-Attention calculation are obtained by linearly transforming the input X by the matrix W, respectively. The query is also calculated by each RIMs using its own transformation matrix W. These matrices W are parameters of the RIMs, and each RIM has its own W to calculate the Query.

In addition, not only the input X of the series information can be easily processed at time t, but also the input with a spatial structure such as images can be used to select the RIMs to be activated by the same procedure if the output of an embedding network such as CNN is treated as X.

Independent RIM dynamics

Here we consider independent dynamics with no information flow between RIMs. There are several possible formats, but the authors adopt the GRU (LSTM) architecture. As shown in the following equation, the state of the kth RIM at time t is denoted as the latent state h_(t,k), and the input is A_k obtained from the Attention calculation described in Section 2.2. Also, since St is a set of activated RIMs, only the activated RIMs update through their own GRU (LSTM).

Communication between RIMs

Basically, RIMs are learning with their own parameters, but RIMs that are activated using the Attention mechanism are provided with a chance to acquire information from other RIMs. The reason for this is that even if the inactive RIMs are not directly related to the input, they may contain information that is useful to the activated RIMs.

As can be seen from the above equation, based on the Attention mechanism introduced in Section 2.1, we introduced a residual connection (h_(t,k)) to prevent gradient loss (latent state h_(t,k) added at the end of Soft-Attention). To achieve sparse information exchange between RIMs, we used top-k Attention as well.

related research

Neural Turing Machine (NTM) and Relational Memory Core (RMC)
NTM uses independent memories with an attention mechanism to read and write. the input information of RIMs only affects a part of the memory. RIMs try to keep the memory as independent as possible, while RMCs use a multi-headed attention mechanism to keep the information flowing between multiple memories. influence each other.
Separate Recurrent Models
EntNet and IndRNNs can be considered as independent recurrent models, but RIMs use attention mechanisms to communicate sparsely.
Modularity and Neural Networks
A neural network can be thought of as consisting of multiple modules, but RIMs allow multiple modules to be activated and to exchange information in a highly efficient manner.
Computation on demand
Many other architectures temporarily suspend the latent representation (h) of the RNN, but RIMs differs from them in that it selects the input information.

experiment

Here we show that RIMs contribute to generalization performance in environments where change occurs or in modular tasks, and then investigate the reasons for this. We begin by examining generalization to time series and object-based generalization and in complex environments that require both.

Generalization performance of time series patterns

First, we visualize that different RIMs are activated for different patterns of time series data; we can see in the middle part of Figure 2 that RIMs are activated in a fixed pattern when no time-series information is input. Next, we describe the copy task and the series MNIST classification task.

In the copying task, where a short string is followed by a long blank, and then the reproduction of the string is evaluated, RIMs can generalize to 50 steps of blank during training and 200 steps of blank during testing, but the comparison methods LSTM, NTM and RMC do not do well (Table 1 left). We show in additional experiments that the elements of RIMs introduced in Chapter 2 are needed to achieve this (Appendix D.1).

In the task of classifying MNIST images with pixel [0,1] sequence inputs, we train on 14x14 images and then perform evaluation experiments at different resolutions: 16x16, 19x19, and 24x24. RIMs outperforms Transformers and other leading methods in the need for long-term memory of information rather than a copying task, and it can be said that the mechanism of RIMs, which respond only to relevant parts, is robust to changes in series length caused by changes in resolution (Table 1, right).

Object-based generalization performance

We then evaluate the object-based generalization performance of RIMs using a task that predicts the motion of banding balls of different sizes and speeds.

Figure 3, left, shows the results of a task in which the RIMs predicted the motion of a ball up to 50 frames after being given a 15-frame movie. Even though the number of balls during training changed during testing and a part of the input was not visible, the RIMs showed lower reconstruction error than the baseline. In addition, RIMs outperformed all comparative methods even when the number of balls was changed from 1 to 6 during training and testing, indicating that RIMs have better object-based generalization performance (Figure 3, right).

Figure 4 also shows that RIMs are more robust than Baseline LSTMs to both known and unknown obstacles in the pickup task in a grid environment.

Generalization performance in complex environments

Spatio-temporal generalization performance was verified in Sections 4.1 and 4.2. The generalization performance in a more complex environment combining these two is verified by Atari games.

Baseline is a method that captures the changing environment using LSTM and outputs the policy using PPO Agent. Since we use a trained PPO Agent, we simply replace the LSTM with RIMs, as shown in Figure 5, which uses a metric that is greater than 0 if the accuracy is better than that of the Baseline. RIMs-PPO is more accurate than LSTM-PPO in many tasks. In particular, in tasks such as Demon Attack, where changes in the environment are highly relevant to the current state, the ability of RIMs to select an appropriate RIM for the environment can contribute significantly to accuracy.

Discussion & Ablation

Experiments have shown that the proposed method RIMs can successfully capture changes in the input. Through additional experiments (see Appendix ), the authors showed that 1. sparse activation 2. Attention to process the input is necessary and 3. communication between RIMs (Section 2.4) contributes to the accuracy.

Summary

Many systems in the world operate under independent mechanisms while occasionally interacting with each other. On the other hand, the authors argue that many machine learning methods, on the contrary, implicitly introduce a bias such that everything is related to the input. Recurrent Independent Mechanisms (RIMs) introduced in this paper are just one example of implementing independent mechanisms in deep learning, but a large number of experiments have shown its effectiveness. We believe that it will be worthwhile to introduce this paper just to remind readers of the idea of independent mechanisms when they are troubled with generalization performance under environmental changes (especially Out-Of-Distribution) in the future.

Categories related to this article

匿名