Activation Function Summary

Survey 24/11/2021

3 main points
✔️ Survey papers on activation functions
✔️ Introduction of various activation functions by classification
✔️ Introduction of experimental results comparing activation functions in image classification, language translation, and speech recognition

A Comprehensive Survey and Performance Analysis of Activation Functions in Deep Learning
written by Shiv Ram Dubey, Satish Kumar Singh, Bidyut Baran Chaudhuri
(Submitted on 29 Sep 2021)
Comments: Submitted to Springer.
Subjects: Machine Learning (cs.LG); Neural and Evolutionary Computing (cs.NE)

code：

The images used in this article are from the paper, the introductory slides, or were created based on them.

first of all

Various activation functions such as sigmoid, tanh, ReLU, etc. have been proposed for use in deep learning.

In this article, we introduce survey papers that provide detailed information about the activation functions proposed so far, including their classification, properties, performance comparison, and other important information. We hope that these papers will be useful for selecting activation functions in deep learning and designing new activation functions.

On the activation function

Initially, activation functions can be classified as follows based on their characteristics and properties.

The Characteristic Type in the figure shows the function that each activation function is based on. Specifically, they are classified into Sigmoid/Tanh-based, ReLU-based, Exponential Unit-based, Learning and Adaptive, and Other.

Within these classifications, the main activation functions are characterized as follows

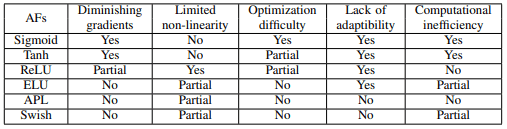
Properties of AFs show the properties of each activation function definition. Specifically, the AFs can be classified according to the following properties: parametric or not, monotonic or not, smooth or not, bounded or not, and range of the output.

Different Applications show what tasks each activation function is used for.

The following sections describe the various activation functions based on the Classification of Characteristic Type.

Sigmoid/Tanh-based Activation Functions

In the early neural networks, (Logistic) Sigmoid and Tanh were mainly used as activation functions. These are represented by the following figures (purple and green lines) and formulas.

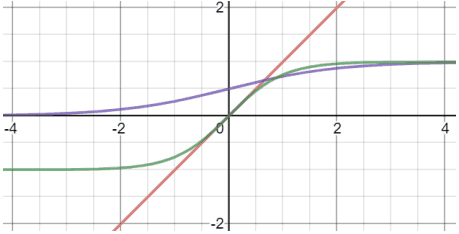
$Sigmoid(x)=1/(1+e^{-x})$

$Tanh(x)=(e^x-e^{-x})/(e^x+e^{-x})$

Both Sigmoid and Tanh functions have some issues such as gradient vanishing and complexity of computation. Activation functions based on these functions can be summarized in the following table.

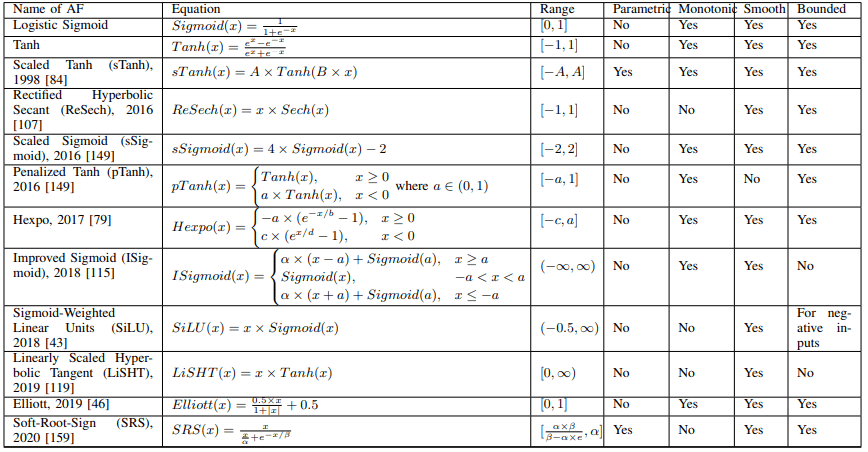
For example, in Scaled Sigmoid(sSigmoid), the performance of Sigmoid is improved by appropriate scaling.

In addition, Penalized Tanh (pTanh) eliminates the uniform slope around the origin by penalizing the negative region of Tanh and shows good performance in natural language processing tasks.

As a case study not shown in the table, the use of noise to cope with gradient vanishing () has also been proposed.

In general, we aim to mitigate the vanishing gradient problem and improve performance by scaling with additional parameters and changing the gradient properties.

ReLU-based activation function

The ReLU function is a very simple activation function expressed as $Relu(x)=max(0,x)$. Compared with Sigmoid and Tanh, this function is very popular in deep learning because of its advantages such as simplicity of computation and less gradient vanishing problem.

The improved ReLU-based activation functions address some of the properties of ReLU, such as the fact that negative values are not used, the nonlinearity is limited, and the output is non-bounded. The ReLU-based activation functions are listed in the table below.

On the non-utilization of negative values in ReLU

First, we present a case study that addresses the fact that ReLU does not use negative values.

A typical example is Leaky ReLU (LReLU), which extends ReLU to the negative region as a linear function with small slope (e.g. $LReLU(x)=0.01x$ for $x<0$). Although LReLU is used in various situations and shows excellent performance, it is difficult to find how the slope of LReLU should be set.

Therefore, derivatives such as Parametric ReLU (PReLU), in which the slope of the negative region is a learnable parameter, and Randomized ReLU (RReLU), in which the slope is randomly sampled from a uniform distribution, have also been proposed.

Parametric Tanh Hyperbolic Linear Unit (PTELU) has also been proposed to use Tanh with learnable parameters for negative regions.

In another direction, Concatenated ReLU (CReLU) utilizes the negative value information by combining the two outputs of ReLU(x) and ReLU(-x).

In addition, Flexible ReLU (FReLU), Randomly Translational ReLU (RTReLU), and Average Biased ReLU (ABReLU), ReLU is based on the average value of learnable parameters or random numbers or features, and the ReLU is translated in the x-axis or y-axis direction by translating it to use negative values.

On the limited nonlinearity of ReLU

Next, we present an example of an improvement in the direction of extending the nonlinearity of ReLU.

In S-shaped ReLU (SReLU), three linear functions and four trainable parameters are used to increase the nonlinearity of ReLU. Similarly, Multi-bin Trainable Linear Units (MTLU) combine a large number of linear functions.

In addition, Elastic ReLU (EReLU) controls the nonlinearity by randomly setting the slope of the positive region.

Another direction exists when ReLU is combined with other functions, such as Rectified Linear Tanh (RelTanh), which combines ReLU with Tanh, or Natural-Logarithm ReLU (NLReLU), which combines ReLU with a logarithmic function.

On the non-bounded output of ReLU

ReLU and its variants of the function can be unstable to learn because the output is non-bounded.

To cope with this point, Bounded ReLU (BReLU) improves the stability of learning by setting an upper limit of the output.

The exponential unit-based activation function

Activation functions using exponential functions were proposed to deal with the problems faced by Sigmoid, Tanh, and ReLU. Among the activation functions classified in this category, ELU, which is a typical one, is defined by the following equation.

ELU combines the advantages of ReLU with increased robustness to noise in the negative region compared to Leaky ReLU and Parametric ReLU.

As activation functions based on this ELU, for example, Scaled ELU (SELU) which scales ELU, Continuously Differentiable ELU (CELU) which enables continuous differentiation for $\alpha \neq 1$, and Parametric Deformable ELU (PDELU) which makes the average value of the activation map close to zero and the Parametric Deformable ELU (PDELU), which makes the mean of the activation map close to zero.

As in the case of ReLU, there are cases where the function for positive inputs is modified to be bounded.

Learning and Adaptive Activation Functions

Next, we introduce activation functions with learnable parameters. Typical examples are Swish, and these are summarized in the table below.

For example, Swish adjusts the shape of the activation function between a linear function and ReLU depending on the learnable parameter $\beta$ (linear if $\beta is small, closer to ReLU if it is large$).

Examples of Swish extensions exist, such as ESwish, flatten-T Swish, and Adaptive Richard's Curve weighted Activation (ARiA).

There are other examples, such as the work here and Adaptive AF (AAF), which combines PReLU and PELU, where multiple activation functions are combined by learnable parameters.

In general, the goal is to control the shape of the nonlinear function by learnable parameters and to combine multiple activation functions to achieve an appropriate activation function for the dataset and network.

Other activation functions

Finally, we introduce activation functions other than the ones mentioned above.

Softplus Activation Function

Softplus is a function defined by $log(e^x+1)$.

An activation function based on this, for example Softplus Linear Unit, combines Softplus and ReLU (\alpha × x for $x \geq 0, \beta × log(e^x+1) for x<0).

Other functions such as Rectigied Softplus (ReSP) and Rand Softplus also use the Softplus function.

Also proposed are Mish activation functions such as the one defined by $Mish(x)=x×Tanh(Softplus(x))$, which is used in the YOLOv4 model for object detection.

Stochastic activation function

There are probabilistic activation functions such as RReLU, EReLU, RTReLU, and GELU.

For example, the Gaussian Error Linear Unit (GELU) is the function defined by $x\Phi(x)$ (where $\Phi(x) = P(X ≤ x), X ~ N (0, 1)$) (which can be approximated as $xSigmoid(1.702x)$).

Other proposed extensions of GELU include the Symmetrical Gaussian Error Linear Unit (SGELU), Doubly truncated Gaussian distributions, and Probabilistic AF (ProbAct) There is also a proposal for the use of the Probabilistic AF (ProbAct).

Polynomial activation function

Activation functions that use polynomials include Smooth Adaptive AF (SAAF), Rectified Power Unit (RePU) ($x \geq 0 for x^s (s is a hyperparameter)$), Pade Activation Unit (PAU), and Rational AF (RAF), etc. exist.

Activation function by subnetwork

In Variable AF (VAF), a small sub-neural network by ReLU itself is used as an activation function.

Similar methods exist such as Dynamic ReLU (DY-ReLU), Wide Hidden Expansion (WHE), and AF Unit (AFU).

Kernel activation function

Kernel-based non-parametric AFs (KAFs) and their extension, multi-kernel AFs (multi-KAFs), exist as examples of expanding activation functions with kernel functions.

On the activation function of SOTA

The activation functions of SOTA for various data sets and models are shown in the table below.

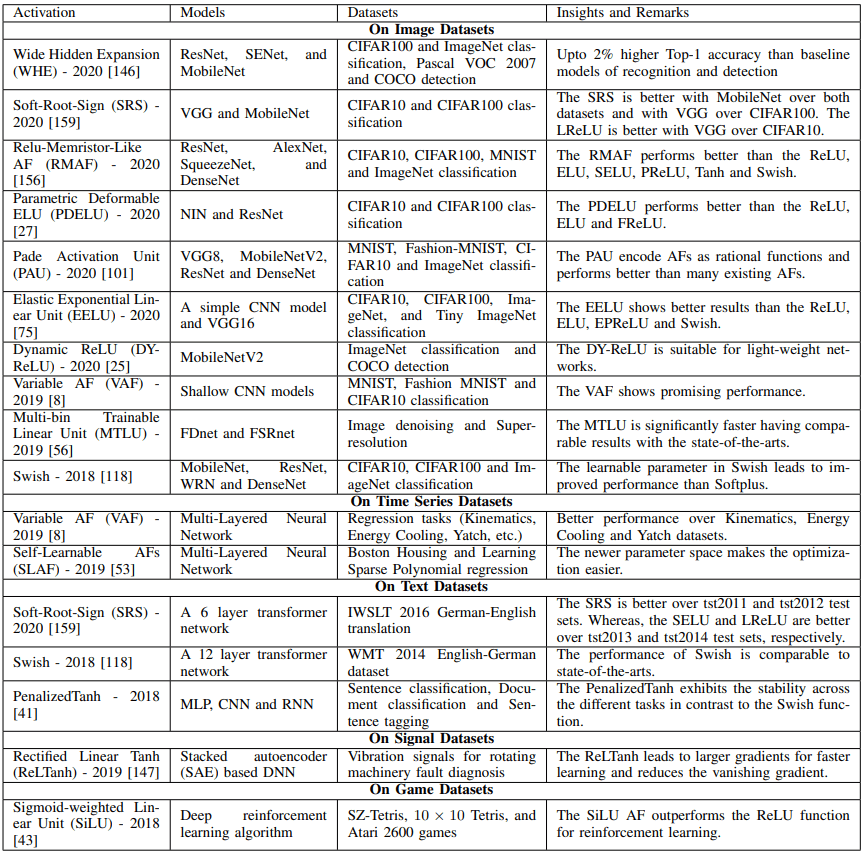
The above table may be helpful to see which activation functions show the best results for which datasets and models. Also, a list of survey papers on existing activation functions is given below.

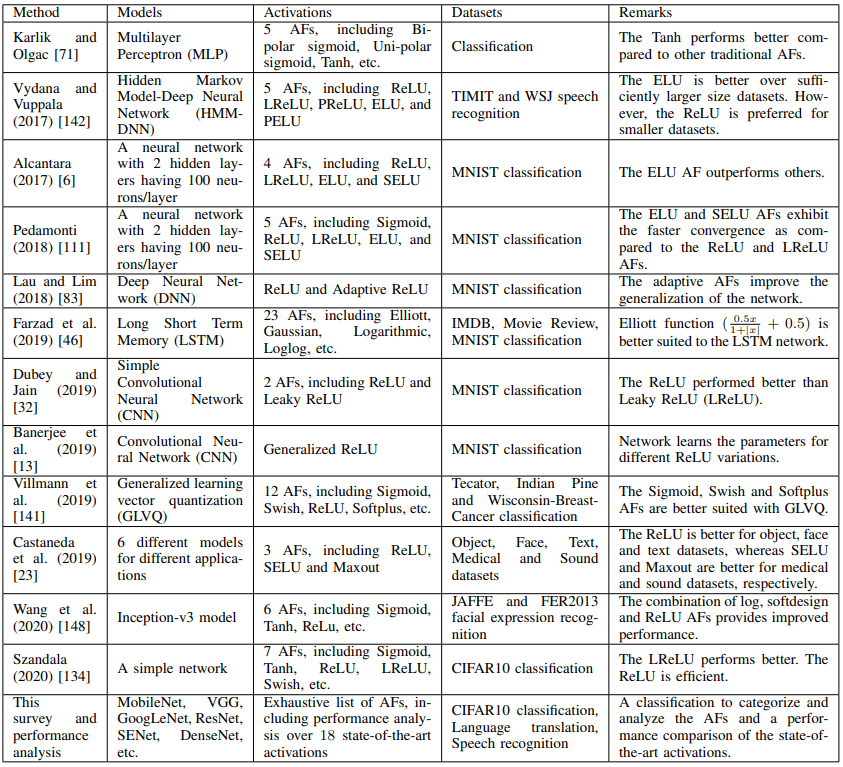
experimental results

In the original paper, we experimented with 18 different activation functions for three tasks: image classification (CIFAR10/100), language translation (German to English), and speech recognition (LibriSpeech). The activation functions used in the experiments are as follows.

Initially, the experimental results in CIFAR10 are as follows.

Next, the experimental results in CIFAR100 are as follows.

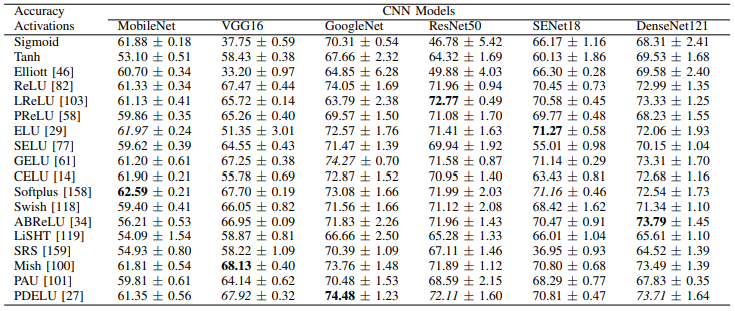
In general, we can see that the optimal loss function is different for each model (e.g. Softplus, ELU, and CELU show superior performance in MobileNet). In addition, the learning time (100 epochs) for each activation function in CIFAR100 is as follows.

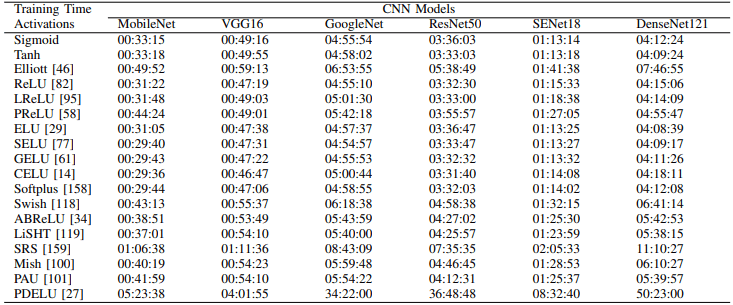
It can be seen that PDELU, SRS, Elliott, etc. are particularly time-consuming. Furthermore, the learning curves for each model in CIFAR100 are as follows.

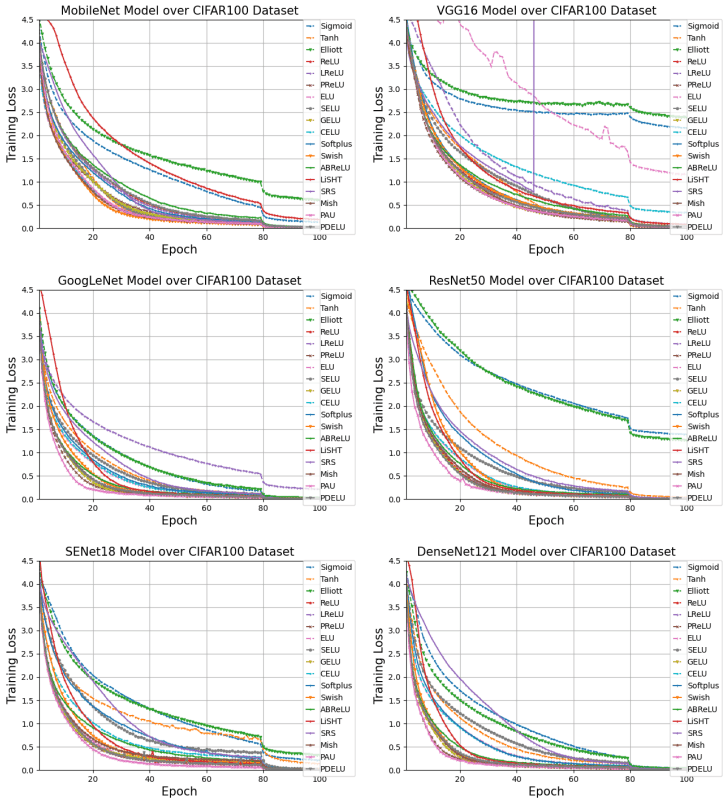
PAU, PReLU, GELU, and PDELU converge particularly fast. Finally, the results on the translation and speech recognition tasks are as follows.

Tanh, SELU, PReLU, LiSHT, SRS, and PAU have shown excellent results in language translation, while PReLU, GELU, Swish, Mish, and PAU have shown excellent results in speech recognition.

summary

In this article, we introduced a survey paper that summarizes important information about various activation functions, including their classification, properties, and performance comparison.

It contains a great deal of information, including comparative experiments of activation functions for each data set and model, and is a very useful paper if you want to get more information about activation functions, so I recommend that you look through the original paper.