拡散モデルを時系列データの欠損補完問題に適用したSSSDモデル

3つの要点
✔️ 実用上で重要な課題である時系列データの欠損の補完に拡散モデルと構造化状態空間モデルを適用
✔️ 今までの補完アルゴリズムでは、欠陥シナリオによって性能が劣っていたのが、このモデルで大きく改善
✔️ 同じメカニズムで、時系列予測問題にも適用

Diffusion-based Time Series Imputation and Forecasting with Structured State Space Models
written by Juan Miguel Lopez Alcaraz, Nils Strodthoff
(Submitted on 19 Aug 2022)
Comments: Published on arxiv.
Subjects: Machine Learning (cs.LG); Machine Learning (stat.ML)

code：  

本記事で使用している画像は論文中のもの、紹介スライドのもの、またはそれを参考に作成したものを使用しております。  

概要

この論文は、時系列データの欠損値の補完について新しい手法を提案するものです。DALL-E2やStable Diffusion等で用いられていることで有名になった拡散モデルをここでは画像ではなく、時系列データに適用しています。実世界の多くのデータ解析業務において、欠損値の補完が必要になることが多いです。本論文では、2つの新しい技術を用いた補完モデルであるSSSDを提案します。２つとは、最先端の生成モデルである（条件付き）拡散モデルと、内部モデル構造化状態空間モデルであり、特に時系列データにおける長期依存性を捉えるのに適しています。SSSDが、先行アプローチが意味のある結果を提供できなかった一時停止-欠落シナリオを含む広範囲の困難なデータセットと、様々な欠落シナリオにおいて、最先端に匹敵するか、それを上回る確率的帰属と予測性能を出力することを実証しています。

はじめに

入力データの欠損の理由は、データ入力の不備、機器の故障、ファイルの紛失など、さまざまです。ほとんどのアルゴリズムは学習するために欠損値のないデータを必要とするため、欠損入力データの処理は機械学習アプリケーションの大きな課題となっています。先行研究で実証されているように、残念ながらデータ補完の品質は下流のタスクに重大な影響を与え、不十分な補完は下流の分析に偏りをもたらすことさえあり、その結果得られた結果の妥当性に疑問を呈する可能性があります。

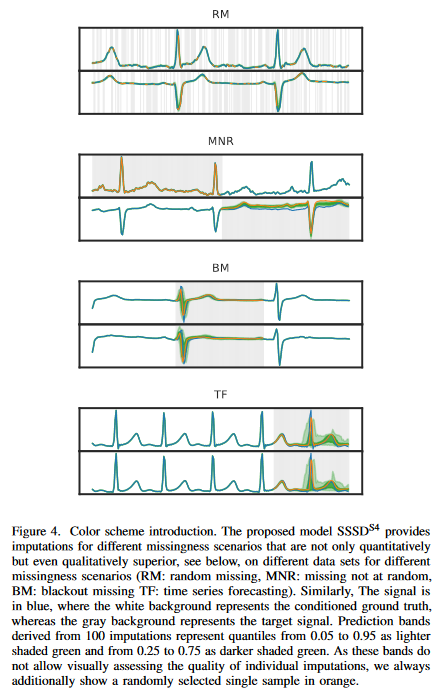
この研究では時系列データに焦点を当てます。そして、様々な欠測シナリオ(Fig. 4)を検討しています。RM: ランダム欠陥、MNR: 非ランダム欠陥、BM: 一時停止欠陥、TF: 時系列予測です。このように、時系列予測は一時停止欠落のケースの一つと見なすことができ、補完ウィンドウの位置がシーケンスの末尾にあるとすれば、統一して議論することができます。また、未指定問題クラスとしての補完を扱う最も現実的なシナリオは、確率的補完法の使用であることも強調します。これは、単一の補完のみを提供するのではなく、様々なもっともらしい補完のサンプルを許可するものです。したがって、摂動ベースの説明可能AI手法の基礎の一つを表す、補完部分の下流アルゴリズムの感度を調べることができます。最後に、予測区間の広さは、データにおける固有の不確実性を定量化する方法を提供します。

時系列補完に関しては、統計的手法から自己回帰モデルに至るまで、膨大な文献があります。最近、深層生成モデルは、長いシーケンスの時系列補完や長いホライズンでの時系列予測問題をモデル化するための有望なパラダイムとして出現し始めました。しかし、多くの既存モデルは、ランダムな欠損シナリオに限定されていたり、学習中に不安定な挙動を示したりしています。あるデータセットにおいて、一時停止欠測シナリオでは、最先端のアプローチですら質的に意味のある補完を提供することさえできていません。

この研究では，時系列の補完のための新しい生成モデルに基づいたアプローチを提案することによって，これらの欠点に対処することを目的とします。本論文では拡散モデル，より具体的には，音声生成の文脈で提唱された DiffWave フレームワークを，異なるデータモダリティにおける生成的モデリングの観点から，現在の最先端として使用します。第二の主要な要素は，モデルの主要な計算構成要素として，拡張畳み込みやトランスフォーマー層の代わりに構造化状態空間モデルを用いることであり，これは特に時系列データにおける長期依存性の処理に適しています。

要約すると、本論文の主な貢献は以下の通りです。

時系列補完用のSTRUCTURED STATE SPACE DIFFUSION (SSSD) モデル

時系列補完

時系列データと同様に、x₀ を R^L×K の形状を持つデータサンプルとする。ここで、L は時間ステップの数、K は特徴またはチャネルの数を表します。このとき、入力データの形状に合わせたバイナリマスク、すなわち、m_imp∈[0, 1]^L×K が一般的で、条件となる値は1、0は補完される値を表します。入力に欠損値がある場合、入力データに存在する値（1）と存在しない値（0）を区別するために、同じ形状のマスクm_mviが追加で必要となります。

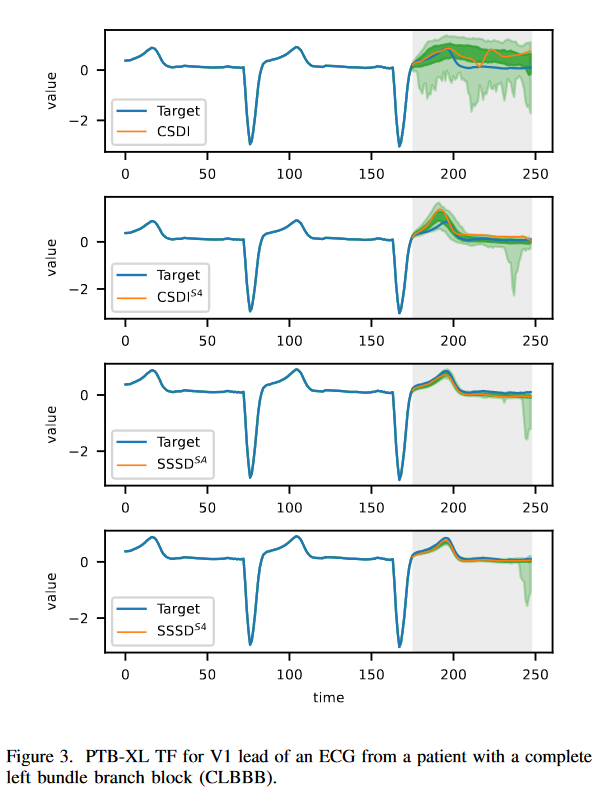
文献で定義している異なる欠落のシナリオを区分しているが，再掲します。ランダムミッシング（RM）を，インピュテーションマスクのゼロエントリが入力サンプル全体の全チャネルにわたって一様分布に従ってランダムにサンプリングされる状況と定義します。次に、MNR（Missing Not at random）は、各KのL次元のx0において、xiの欠落したランダムな部分集合を仮定しています。最後に，ブラックアウトミッシング（BM）は，L次元のx0におけるxiの欠損部分集合がすべてのKについて存在すると仮定します。 前述のように，時系列予測（TF）はBM補完の特殊ケースであり，補完領域はt時間ステップの連続領域に及びます。信号の色は青で、白い背景は条件付きのグランドトゥルースを表し、灰色の背景はターゲット信号を表しています。補完から得られる予測バンドは、0.05から0.95の分位を薄い緑色、0.25から0.75の分位を濃い緑色で表しています。これらのバンドは、個々の補完の品質を視覚的に評価することができないので、ここでは常にランダムに選択された単一の補完サンプルをオレンジ色で追加表示します。

拡散モデル

拡散モデルは、画像から音声やビデオデータまで、様々なデータモダリティにおいて最先端の性能を示した生成モデルの一種です。拡散モデルは、いわゆる順過程でマルコフ的に逐次追加されるノイズを逆過程で除去することを逐次学習することにより、潜在空間から信号空間への写像を学習するものです。したがって、この2つの過程が拡散モデルの骨格となります。順過程は次のようにパラメータ化されます。

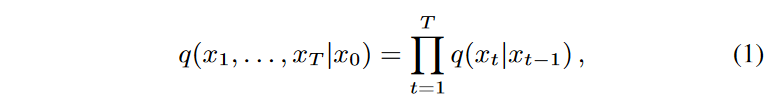
ここで q(xt|xt-1) = N (xt; √1 - βtxt-1, βt1) とし、（固定または学習可能な）順過程の分散 βt はノイズレベルを調整するものです。等価的に、xt は、∼N (0, 1) に対して xt = √αtx0 +(1-αt) と閉形式で表すことができ、ここで αt = ∑t i=1(1 - βt) とすることができます。

逆過程は次のようにパラメータ化されます。

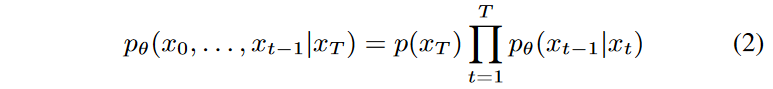
ここで、x_T ∼ N (0, 1)です。ここでも、pθ(xt-1|xt)は、学習可能なパラメータを持つ正規分布（対角共分散行列を持つ）として仮定されます。Hoらは、pθ(xt-1|xt) の特定のパラメータ化を用いて、以下の目的語を用いて逆行列を学習できることを示しました。

ここで、Dはデータ分布を意味し、θ(xt, t)はニューラルネットワークを用いてパラメータ化されます。この目的は、tが小さいとき、すなわちノイズレベルが小さいときの項の重要度を低くする、負の対数尤度の重み付き変分限界として見ることができます。

これまで述べてきた無条件拡散過程を拡張して、逆過程が付加的な情報、すなわち，θ＝θ（xt，t，c）を条件とする条件付き変形を考えることができます。ここで，条件情報cの正確な性質は、その時のアプリケーションに依存し、グローバルラベルからスペクトログラムまでの範囲です。ここでは、それは入力（補完マスクに従ってマスクされた）と補完マスク自体の連結によって与えられる、すなわち、c = Concat(x0 (m_imp m_mvi), (m_imp m_mvi))。（ここで、はポイントワイズ乗算を表す)。この研究では、拡散処理を全信号に適用する場合と、補完する領域のみに適用する場合の2種類のセットアップ（それぞれD0、D1と表記）を検討します。いずれにせよ、式（3）の損失関数の評価は、グランドトゥルースが利用可能な入力値、すなわちm_mvi = 1にのみ行われるものとします。D0では、これは（条件付けが可能な）補完マスクの非ゼロ部分に対応する入力値に対する再構成損失、および補完マスクが消滅する入力トークンに対応する補完損失とみなすことができます。D1では、再構成損失は構造上消滅します。

Tashiro ら と同様に、筆者らは DiffWave アーキテクチャ に基づいて θ(xt, t, c) のパラメタリゼーションを行います。Tashiroらとは異なり、ここでは形状の拡張された4次元内部表現（バッチ次元、拡散次元、入力チャネル次元、時間次元）を扱いません。これは、後述するトランスフォーマーや構造化状態空間モデルなどの逐次データのための多くの最新のアーキテクチャが逐次、すなわち3次元入力バッチのみを処理できるため、時間次元と特徴次元を交互に処理する必要があるためです。ここでは、入力チャネルを拡散次元にマッピングし、時間次元に沿った拡散のみを行うという、より概念的に単純な方法をとります。つまり、（バッチ次元、拡散次元、時間次元）の形状のバッチを処理します。さらに、元のアーキテクチャで使用されている拡張畳み込みよりも時系列データの処理に適しているS4層を使用してDiffWaveアーキテクチャの内部を変更します。

状態空間モデル

最近導入された構造化状態空間モデル（SSM）は、特に時系列における長期依存性を捉えるための非常に有望なモデリングパラダイムを表しています。この形式は、1次元の入力系列u(t)をN次元の隠れ状態x(t)を介して1次元の出力系列y(t)に接続する線形状態空間遷移方程式を中核とします。この遷移式は次のように表されます。

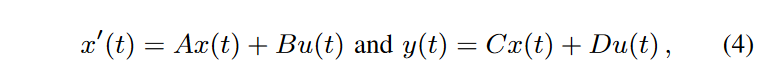
ここで、A, B, C, D は遷移行列です。離散化後、入力と出力の関係は畳み込み演算として書くことができ、最新のGPUで効率的に評価することができます。長期依存性を捉える能力は、HiPPO理論に従ったA∈R^N×Nの特定の初期化に関するものです。構造化状態空間モデル（SSM）では、上記のSSMブロックの複数のコピーに、適切な正規化層と点順完全連結層をトランスフォーマー層のスタイルで積み重ねることにより、構造化状態空間シーケンスモデル（S4）を提唱し、様々なシーケンス分類タスクで優れた性能を実証しています。実際、得られたS4層は、データと形状（バッチ、モデル次元、長さ次元）の形状保存マッピングをパラメータ化するため、トランスフォーマー層、RNN層、1次元畳み込み層のドロップイン置き換えとして（適切なパディングで）使用することが可能です。S4層をベースに、U-netに触発された構成でS4層を組み合わせることで得られる、シーケンス生成のための生成モデルアーキテクチャSaShiMiが発表されました。このモデルは自己回帰モデルとして提案されたが、著者らは既にDiffWave のような最先端の非自己回帰モデルのコンポーネントとして（非因果）SaShiMiを用いることが可能であると指摘しています。

提案手法

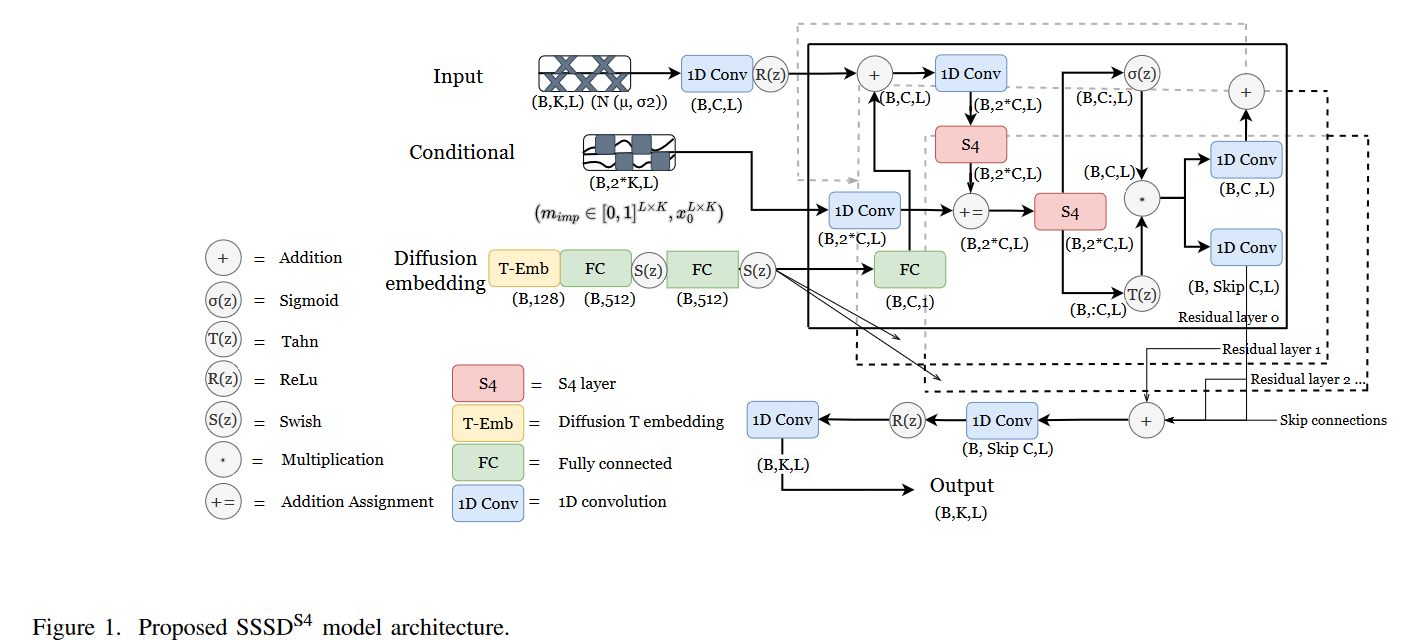
筆者らは、Diffwave に基づく拡散モデルとして、3つの異なる変型を提案しています。まず、条件付きDiffWave-variant であるSSSD^S4を提唱し、双方向の拡張畳み込みの代わりに、拡散埋め込みを加えた後のその各残留ブロック内の拡散層としてS4層を置き換え、適合させました。第二の修正として、条件情報との加算割り当ての後に第二のS4層を含めることで、処理済み入力と条件情報を結合した後にモデルにさらなる柔軟性を与えます。このアーキテクチャはFig. 1に模式的に示されています。第二に、SSSD^SAと名付け、SaShiMiアーキテクチャの非自己回帰を適切な条件付けにより時系列代入のために拡張することを探求しています。第三に、CSDIアーキテクチャを改良し、時間方向に動作するトランスフォーマー層をS4モデルで置き換えたCSDI^S4について検討します。このように、筆者らは、時系列の領域により適応したアーキテクチャの潜在的な改善点を評価することを目的としています。

関連研究

深層学習に基づく時系列補完

時系列補完の完全な議論は、深層学習の文献だけでさえ、この仕事の範囲を明らかに超えているため、このトピックに関する最近のレビューを参照してください。深層学習ベースの時系列補完手法は、使用される技術に基づいて大まかに分類することができます。

(1）BRITS、GRU-D、NAOMI、M-RNNなどのRNNベースのアプローチは、時系列のモデルに単一または多方向のRNNを使用しています。しかし、これらのアルゴリズムは、多様な学習制限に苦しみ、最近の研究で指摘されているように、それらの多くは、多様な欠損シナリオや異なる欠損率において、最適ではない性能しか示さないかもしれません。

(2) 生成モデルは、この分野における第二の主要なアプローチです。これには、E2-GAN 、GRUI-GAN などのGANベースのアプローチや、GP-VAE などのVAEベースのアプローチなどがあります。これらの多くは、学習が不安定であり、最先端の性能に到達できないことが分かっています。また、最近、筆者らの研究に最も近い競合であるCSDIのような拡散モデルも検討され、非常に強い結果が得られています。

(3) 最後に、グラフニューラルネットワーク（GRIN）、順列等価ネットワーク（NRTSI）、時間・特徴相関を捉える自己注意（SAITS）、制御微分方程式ネットワーク、序数微分方程式ネットワークなど、現代のアーキテクチャに依拠したアプローチ群が存在します。

拡散モデルによる条件付き生成モデリング

拡散モデルは，特に画像領域において，インペインティングなどの関連するタスクに使用されてきました。適切な修正により，画像領域からのこのような手法は，時系列領域にも直接適用することができます。音は非常に特殊な時系列であり，異なるグローバルラベルやメルスペクトログラムを条件としたDiffWave のような拡散モデルは，異なる音声生成タスクにおいて優れた性能を示しました。一般的な時系列に戻ると、既に上述したように、最も近い競合はCSDI です。2つのアプローチの主な違いは、(1) トランスフォーマーの代わりにSSMを使用すること、(2) 特徴と時間方向ではなく，時間方向のみの拡散プロセスの概念的により簡単なセットアップされること、(3)インプットされるセグメントのみをノイズ除去するという異なる学習目的(D1)です。すべての実験において、CSDIと比較しています。

時系列予測

上述のように、時系列予測は一時停止欠陥(BM)シナリオにおける時系列補完の特別なケースと見なすことができます。時系列予測に関する文献は、時系列補完に関する文献よりもさらに豊富です。一方では、LSTNetやLSTMaのような再帰的な一般的なアーキテクチャがあり、他方では、エンコーダ・デコーダ設計による非常に新しいトランスフォーマベースのInformer のような最新のアーキテクチャがあり、これらは長い系列予測で優れた性能を示しました。同様に、GP-Copula 、Transformer MAF 、TLAE などの多様な手法が大きく貢献しています。

実験

実験手順

本論文では（入力）チャンネル次元を拡散処理中に明示的な次元として保持せず，チャンネル次元を拡散次元にマッピングすることによって暗黙的に保持するだけです。これは，シングルチャンネルのオーディオデータ用に設計されたオリジナルのDiffWaveのアプローチに触発されたものです。後述するように、このアプローチは入力チャンネル数が約100チャンネル以下に制限されているシナリオにおいて優れた結果をもたらします。これは，例えばヘルスケア領域におけるECGやEEGといった典型的な単一患者のセンサデータをカバーします。入力チャンネル数が多くなると、モデルはしばしば収束せず、例えば入力チャンネルを分割するなど、異なる学習戦略に頼らざるを得なくなります。このため，本研究の主な実験的評価は、入力チャンネル数が100未満のデータセットに焦点を当てています。

ここでは常に同一の欠落シナリオと比率で補完モデルを学習・評価します。例えば、20%のRMで学習し、同じ設定に基づいて評価します。本研究でデータセットを多様化した理由は、提案手法、特にSSSD^S4が多様な定性的データと多様なベースラインに対して堅牢であることを示すためであり、そのために、重要度の高いシナリオで本手法が信頼できることを示すためにヘルスケア関連のデータセットで実験を実施しました。この研究で利用される性能メトリックは多様です。すべての場合において、スコアが低いほど良い補完結果であることを意味します。ほとんどの場合、単一の補完とグランドトゥルースを比較しており、他のものは補完分布を組み込み、したがって確率的補完に特有のものになっています。

時系列補完

提案したPTB-XL ECGデータセットにおいて、SSSDS4は最新の補完器を上回る性能を発揮する

最初のデータセットとして、PTB-XLデータセットからの心電図(ECG)データを検討します。ECGデータは、ランダムな欠落シナリオを超える首尾一貫した補完を生成するために、いくつかの拍動にわたる信号の一貫した周期構造を捕らえる必要があるため、興味深いベンチマークケースを表しています。ECG信号をサンプリングレート100Hzで前処理し、L = 250タイムステップ（SSSD^SAの場合は248）を考慮しました。RM、NRM、BMの3種類の欠測シナリオを検討しました。CSDI^S4、SSSD^SA、SSSD^S4などの拡散モデルについて、学習目的D0とD1の両方について適用可能かどうかを検討した結果を示します。ベースラインとして、決定論的なLAMC 、強い確率的ベースラインとしてCSDI 、オリジナルのDiffWaveアーキテクチャの条件付き適応を考慮しました。テストサブセットの各サンプルに対して生成された 10 サンプルの MAE，RMSE，CRPS の平均を報告します。

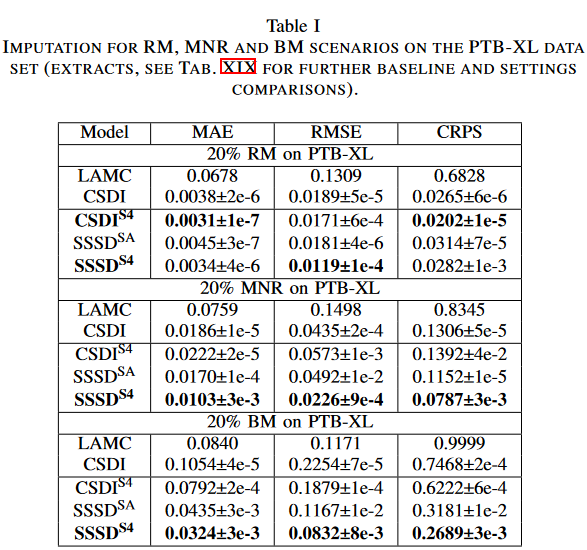
 全てのモデルタイプと欠陥シナリオにおいて、拡散プロセスをインプットされるサンプルの一部に適用すると（D1）、サンプル全体に適用した拡散プロセス（D0）より一貫して良い結果が得られます。そこで、以下では、D1の設定に限定して説明します。提案するSSSD^S4は、ほとんどのシナリオで他の補完モデルを大きく上回り、特にBMではCSDIと比較してMAEが50%以上削減されることがわかりました。BMシナリオでは，SSSD^S4はターゲットCDFに対する補完の累積分布関数（CDF）の差が小さく、CRPSは0.2689であるのに対し、CSDIは0.746でした。同様に，ベースラインとしてDiffWaveが非常に強力な結果を示し、いくつかのシナリオでは、より技術的に進んだSSSD^SAと同等であるにもかかわらず、提案するSSSD^S4はすべての設定において時系列の帰属と生成に明確な改善を示しているのは注目すべきです。また、CSDI^S4のS4層はRMとBMの設定においてCSDIに明確な改善をもたらし、特にRMシナリオにおいてCSDI^S4は低いMAEとCRPSで他の手法より優れていることが示されました。本手法は、CSDIアプローチは、特徴量と時間の一貫性を達成しなければならないRM設定において有用であり、一方、SSSD^S4とその変形は、時間依存性のモデル化が最も重要であるMNRとBM（と後述のTF）において明確な利点を示すと仮定しています。

既存のアプローチでは、意味のあるBM補完を生成できない

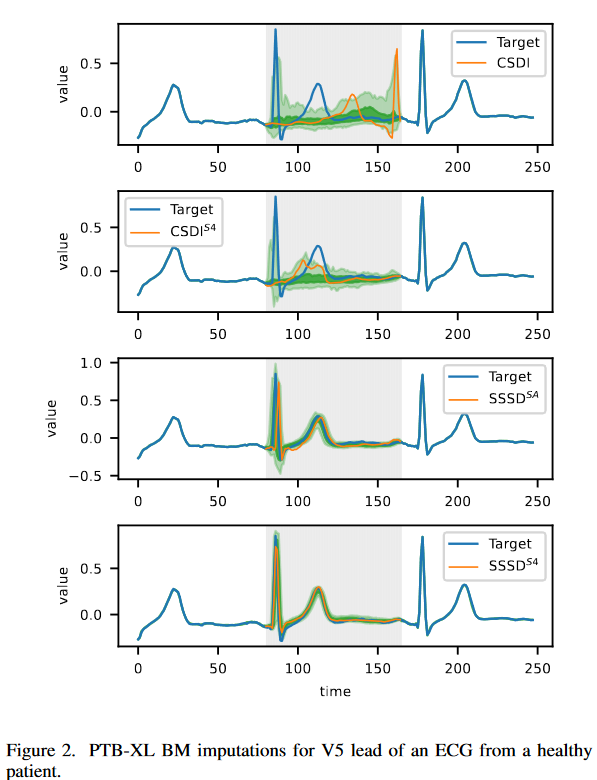
Fig. 2は、PTB-XL補完タスクのモデルのサブセットに対するBMシナリオの補完を示したものです。主な目的は、提案するアプローチによって達成された改善が、肉眼でもわかるような優れたサンプルにつながることを実証することです。左上の図は、最新の補完が意味のある補完を生成できないことを示しています。例として、0.08秒から0.12秒の範囲内の持続時間を持つQRS複合体の識別は正常信号と見なされますが、モデルは複合体を検出できず、むしろ誤ったRピークを表示しています。CSDI^S4では質的な向上は見られるが、本質的な信号の欠落が見られます。SSSD^SAとSSSD^S4の2つのモデルのみが、すべての本質的な信号の特徴を捉えます。SSSD^S4は、タスクに優れており、正常なECGサンプルに期待されるように、よく制御された分位バンドを示す、定性的には最良の結果を達成することができます。

SSSD^S4は、他のデータセットや高い欠損率に対して、最先端のアプローチと比較して競争力のある補完性能を示しています。

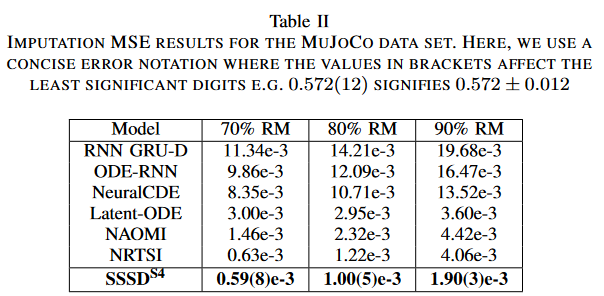
SSSD^S4の優れた性能がさらなるデータセットに及ぶことを示すために、NRTSIからMuJoCoデータセットを収集し、70%、80%、90%といった非常に疎なRMシナリオでSSSD^S4をテストし、それに対して、ベースラインのRNN GRU-D, ODE-RNN, NeuralCDE, Latent-ODE, NAOMI, および NRTSI と性能を比較しました。本研究では3回の試行におけるテストセット上のサンプルごとの単一補完の平均MSEを報告します。ベースラインの結果はすべてNRTSIから収集したものです。

Table IIはMuJoCoデータセットにおける経験的RM結果を示しており、SSSD^S4はすべての欠落シナリオにおいてすべてのベースラインを上回り、特に最も高いRM比90%において、SSSD^S4は50%以上のエラー削減を達成しました。本論文は、実験で明確に示されたように、SSSD^S4がバックワード変性プロセスの時系列信号から適切に再構成できるためには条件値の小さな割合で十分だという仮説を立てています。

高次元データセットにおけるSSSD^S4の性能

また、100チャンネル以上のデータセットに対して、上記の単純だが最適とはいえないチャンネル分割戦略に従って、SSSD^S4の可能性を探りました。

本手法は、10%、30%、50%の異なる欠落率で370の特徴を含むSAITSのElectricityデータセットにRM補完タスクを実装しました。ベースラインとして、M-RNN, GPVAE, BRITS, SAITS と SAITSの変種を使用しました。3回の試行でテストサンプルごとに生成された1サンプルからの平均的なMAE、RMSE、MREを報告します。

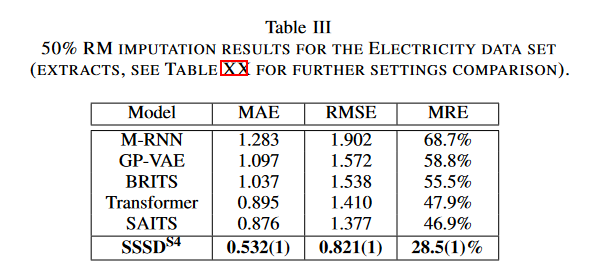
Table IIIに示すように、SAITSはMAE，RMSE，MREそれぞれ0.876，1.377，49.9%を示したが、SSSD^S4では0.532，0.821，28.5%となり、それぞれ39.3，40，39.2%の大幅なエラー削減を達成することができました。残りのRM設定についても、SSSD^S4は有意な誤差低減を示しました。同様に、GRINの25%RMタスクについて、PEMS-BayとMETR-LAデータセットでテストしました。PEMS-Bayデータセットにおいて、SSSD^S4はMICE、rGAIN、BRITS、MPGRU などの確立されたベースラインよりもMAE、MSE、MREの3指標で優れていたが、最近提案されたGRIN にのみ負かされる結果でした。METR-LAデータセットでは、SSSD^S4は再びGRINに劣るが、残りのモデルと同程度でした。

時系列予測

提案データセットでのSSSD^S4

CSDI, CSDI^S4, SSSD^SA, SSSD^S4モデルを2つのデータセットで実装しました。両者について、3回の試行でテストサンプルごとに生成された10個のサンプルに対する指標として、MAE、RMSE、CRPSを報告します。最初に、本研究では再び100Hzでサンプリングされた前からのPTBXLを再考した、しかし、このタスクのためにサンプルあたりL = 1000タイムステップで、800タイムステップで条件付け、200で予測しました。SSSD^SAはMAEとCRPSをそれぞれ0.087と0.557で上回り、SSSD^S4は0.090と0.633とわずかに大きな誤差を達成しました。SSSD^S4はRMSEにおいて0.219と優れており、CSDI^S4は3つの指標においてCSDIより小さい誤差を達成しています。Fig. 3に示したサンプルでも、肉眼で確認できるほど明らかな改善が見られます。

SSSD^S4は、様々なデータセットにおいて、最先端のアプローチと比較して競争力のある予測性能を発揮します

本研究ではGluonTSから収集したSolarデータセットで、条件値と予測地平線がそれぞれ168と24時間ステップである予測タスクでテストしました。ベースラインとして、CSDI、GP-copula、Transformer MAF (TransMAF) 、TLAE を検討しました。すべてのベースラインの結果は、それらのオリジナルの論文から収集したものです。3回の試行でテストサンプルごとに生成された10サンプルのMSEとCRPSの平均を報告します。

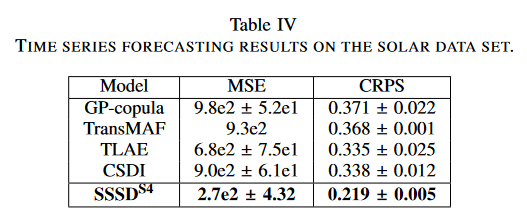
太陽電池データセットの実証結果では、MSEでTLAEが6.8e2であるのに対し、SSSD^S4は2.7e-2を達成し、60%の誤差削減を達成しました。同様に、確率的指標CRPSについても、最強のベースラインであるTLAEが0.335を報告したのに対し、SSSD^S4は0.219を達成し、約34%の大幅な誤差の削減を実現しました。

最後に、長周期予測のための従来のベンチマークデータセットで、SSSD^S4の巧みさを実証しました。本研究はInformerから前処理されたETTm1データセットを収集し、5つの異なる予測設定において予測に使用しました。予測長は24、48、96、288、672時間ステップで、条件値はそれぞれ96、48、284、288、384時間ステップでした。本研究は、ベースラインとして、LSTnet, LSTMa, Reformer, LogTrans, Informer とその変種の一つ Informer(†) と比較しました。本論文では、2 回の試行で生成されたテストサンプルに対する MAE と MSE の平均を報告します。

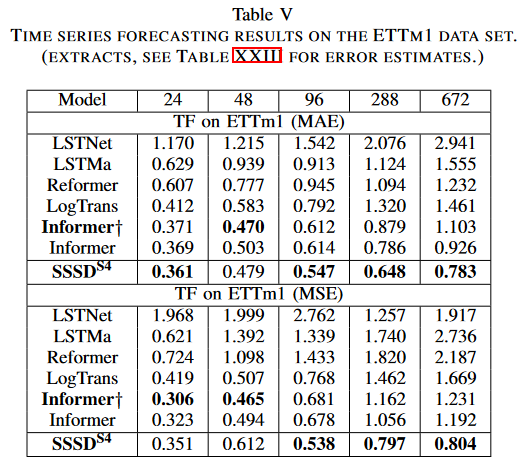
実験結果は、SSSD^S4 のロバストな予測能力、特に、条件付き時間ステップが増加するロングホライズン予測について、再度確認することができました。最初の設定では、SSSD^S4 は MAE において他のベースラインを上回ったが、MSE においては Informer† のスコアと僅差でした。2番目の設定では、短い予測条件と目標長では、SSSD^S4はInformerとInformer†と同程度であるが、残りの3つの設定では、SSSD^S4は残りのベースラインよりも誤差を大幅に削減し、例えば、MAEとMSEでそれぞれ0.783と0.804を得て、最強ベースラインのInformerと比較して、それぞれ0.926と1.192でした。

まとめ

本研究では、長期依存性を持つ逐次データに対する新たなモデルパラダイムである構造化状態空間モデルと、生成モデルに対する現在の最先端アプローチの一つである拡散モデルの組み合わせを提案しています。SSSD^S4は、入力チャンネル数が大きくなりすぎない限り、様々な欠測シナリオの下で、既存の最新鋭の補完を様々なデータセットにおいて性能向上させ、特に一時停止欠測や予測シナリオにおいて高い性能を発揮することがわかりました。特に、補完品質の質的向上が肉眼で確認できる例を示しました。提案技術は、時系列領域における生成モデルのための非常に有望な技術であり、グローバルなラベルから意味分割マスクのようなローカルな情報まで、様々な種類の情報を条件とする生成モデルを構築する可能性を開き、それによってさらに下流の幅広いアプリケーションを可能にします。

• 
• 
• 

この記事に関するカテゴリー

• 論文
• 時系列
• Time-series
• Diffusion Model