用机器学习发现费曼的物理方程式：AI Feynman

神经网络 31/08/2021

三个要点
✔️ 通过反复转化为更简单、更少变量的问题来解决问题。
✔️ 用神经网络改善函数识别问题
✔️ 实现超越现有软件的预测精度

AI Feynman: a Physics-Inspired Method for Symbolic Regression
written by Silviu-Marian Udrescu (MIT), Max Tegmark (MIT)
(Submitted on 27 May 2019 (v1), last revised 15 Apr 2020 (this version, v2))
Comments: Published on arxiv.
Subjects: Computational Physics (physics.comp-ph); Artificial Intelligence (cs.AI); Machine Learning (cs.LG); High Energy Physics - Theory (hep-th)

code：

本文所使用的图片要么来自该文件，要么是参照该文件制作的。

简介

1601年，开普勒试图根据数据解释火星的轨道，在经过40次不成功的尝试后，发现火星的轨道是一个椭圆。这是一个符号回归的例子，即找到一个符号表达式，与一组特定的数据相匹配。

最简单的符号回归是线性组合的线性回归，但一般的符号回归问题仍未解决。其原因是，当一个函数被编码为一串符号时，它随着字符串的长度呈指数增长，使得测试所有字符串在计算上是不可行的。

遗传算法是解决如此大的搜索空间中的问题的一种方式，并在Eureqa软件中实现，它在符号回归问题上取得了成功。

在这项研究中，我们用神经网络进一步改进了这种最先进的技术。我们发现了隐藏的简单性，如神秘数据的对称性和可分离性，并将困难问题递归为变量较少的简单问题。

算法

一般的函数f是非常复杂的，几乎不可能通过符号回归来发现。然而，在物理学和许多其他科学中出现的函数往往具有简化的特性，使它们更容易被发现，例如

(1) 单位
函数f和它所依赖的变量有一个已知的物理单位。这样就可以进行维度分析，有时还可以将问题转化为一个独立变量很少的简单问题。

(2) 低度多项式
f（或它的一部分）是一个低度多项式。这样你就可以通过解同步方程来确定多项式系数，快速解决问题。

(3) 单调性
f是一个基本函数的小组合，每个函数通常不超过两个参数。　这使得我们可以将f表示为具有少量节点类型的分析树。

(4) 平滑性
f是连续的，可能是分析的。这使得使用神经网络对f进行近似计算成为可能。

(5) 对称性
f表示相对于变量的翻译、旋转或缩放的对称性。这个问题可以转化为一个只有一个自变量的简单问题。

(6) 可分割性
f可以写成没有共同变量的两个部分的和或积。通过将自变量划分为相互之间的基本集合，问题可以转化为两个简单的集合。

图中显示了该算法。

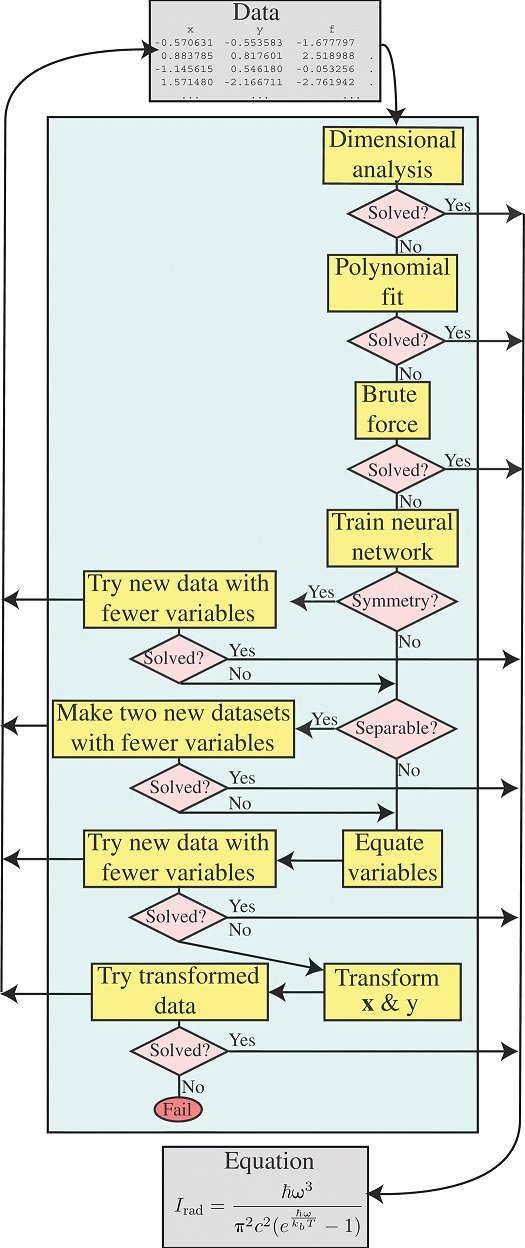
这与人类科学家的做法相同，依次采取不同的策略，一次一个，如果不能一次解决，就分成不同的部分。

下图显示了一个例子，说明如何解决有九个变量的牛顿万有引力定律。

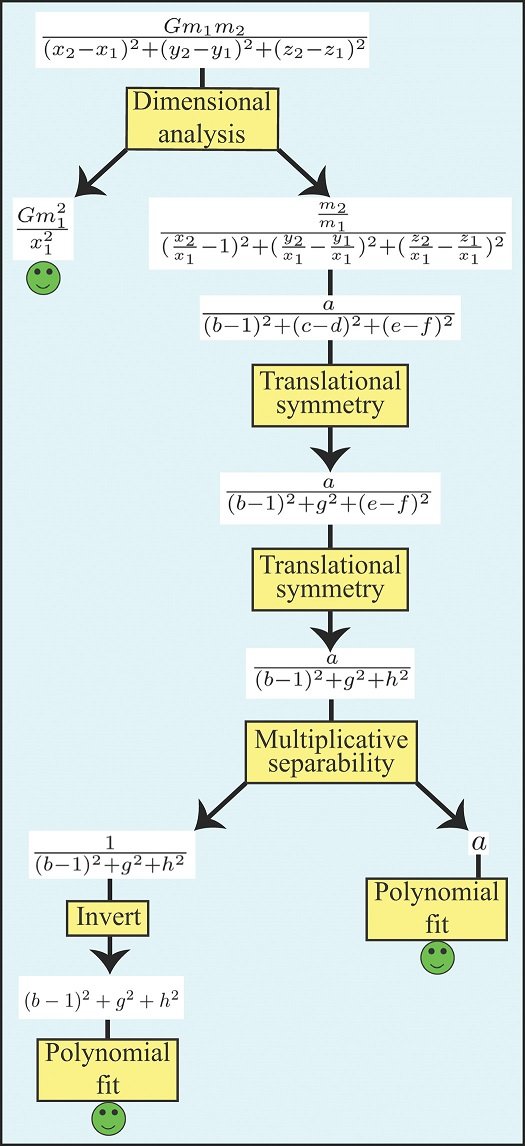
三维分析

尺寸分析模块利用了这样一个事实，即物理学中的许多问题可以通过假设方程两边的单位重合来简化。这通常会将问题转化为具有少量变量的简单问题，这些变量都是无尺寸的。

多项式拟合

建议的方法使用解决同步线性方程的标准方法来寻找最佳多项式系数。

蛮力

蛮力符号回归模型原则上可以解决所有的未知数，但在大多数情况下，从计算的角度来看这是不现实的。一旦未知数据被转化/分解为较简单的部分，蛮力法通常是最有用的。

基于神经网络的测试

即使应用了维度分析，许多数据也过于复杂，无法在合理的时间内通过多项式拟合或Brute force来解决。例如，为了测试函数f是否存在平行移动，我们需要测试f(x1,x2)=f(x1+a,x2+a)，但通常数据集没有该变量的区间，因此需要在数据点之间进行精确的高维插值来执行测试。

为了获得这样一个插值函数，一个神经网络被训练为在给定输入时预测输出。

这有时比其他许多情况下更容易，因为神经网络并不关心数据在某一领域之外是否有很差的概括性。只要它在这个领域内非常准确，它就能达到正确分解可分离函数的目的。

数据库

为了能够对这一算法和其他符号回归算法进行定量测试，我们创建了一个6千兆字节的费曼符号回归数据库（FSReD），可从https://space.mit.edu/home/tegmark/aifeynman.html免费下载。并从以下网站提供免费下载

为了从广泛的物理学科中提取方程样本，我们使用巧妙的费曼物理学讲座中的100个方程生成了一个数据库。除此之外，我们还从其他原版物理书中抽取了20个更具挑战性的方程式。我们把这些称为红利之谜。

结果的比较

AI Feynman和Eureqa算法都被应用于Feynman数据库以进行符号回归，并对每个数据使用多达2小时的CPU时间进行比较。结果显示，Eureqa解决了71%的案件，而AI Feynman解决了100%的案件。

对结果的仔细研究表明，Eureqa无法解决的问题是针对最复杂的数据。

在没有维度分析模块的情况下重新运行AI Feynman时，神经网络更加重要，因为它们可以通过发现对称性和分离性来消除变量。该神经网络通过寻找可分离性和对称性，解决了93%的费曼方程。

AI Feynman随着进程的推进，迭代地减少独立变量的数量，实际上保证了它在正确的方向上前进。相比之下，Eureqa等遗传算法通过连续找到更好的近似值来取得进展，但不能保证更准确的符号表示会更接近真相。

如果Eureqa在完全不同的函数形式中找到一个相当近似但不确切的表达，就有可能落入该局部解决方案。这反映了遗传学方法的一个基本挑战。

数据大小的影响

为了研究改变数据集大小的影响，每个数据集的大小被反复减少10倍，直到AI Feynman失败。即使只使用10个数据点，大多数方程也能通过多项式拟合和Brute force检测出来。

如果真正的方程很复杂，算法可能会过度拟合并 "找到 "错误的方程，在某些情况下需要多达100个数据点。

需要用神经网络解决的方程需要大量的数据点（100到1000000），以使网络能够足够准确地学习未知函数。

噪声的影响

由于在大多数情况下，实际数据会受到测量误差和其他噪音的影响，因此在其因变量y中加入了一个正常的随机数。

从0.000001增加噪音水平，直到AI Feynman失败。大多数方程可以用低于0.0001的数值准确恢复，但有一半可以用0.01的数值解决。

奖金之谜

之前的100个方程应被视为训练集，因为为了优化AI Feynman算法的性能，实施和超参数已经被改进。相比之下，20个红利之谜可以被视为一个测试集，因为它们是在AI Feynman算法及其超参数设置好之后进行分析的。虽然Eureqa只解决了15%的奖金之谜，但AI Feynman解决了90%的奖金之谜。

奖金之谜的成功率差异如此之大，这反映了方程式的复杂性越来越高，需要基于神经网络的策略。