ニューラルネットワークの分類器の境界面を使って3D物体を表現する
3Dの物体の表現方法として、ボクセル、点群やメッシュをつかった手法などが一般的に使われていました。論文では、ニューラルネットワークの分類器の境界面を使って3D物体を表現するという新しい方法が提案されています。
【論文】Occupancy Networks: Learning 3D Reconstruction in Function Space
3D表現における課題
最近では、生成モデルが高解像度画像の生成において驚くべき成功を収めていますが、これらの多くが2D画像として表現されたものです。
しかし、私たちが住んでいる物理的な世界は二次元ではなく三次元です。AIが3D環境と上手く相互作用するためには、3次元での推論が非常に重要です。例えば、ロボットナビゲーションを考えてみましょう。ナビゲーションするには、ロボットはその環境を3Dで再構築し、この3D表現をデータ効率の良い方法で保存しなければなりません。
3D再構成するにあたって、今までいくつかの3D出力表現が提案されてきました。しかし、 2D表現とは対照的に、メモリ効率がよく、データから効率的に推論することができる3D出力表現は依然として難しいままです。
voxel(ボクセル)
voxelは、pixelを3Dに一般化したものです。 2Dイメージ(画像)を拡張しただけなので、その単純さから最も一般的に使用される表現です。
グリッドに従って3D空間を3Dセルに分割しますが、各ボクセルまたはグリッドセルのサイズによって表示の精度が決まってしまいます。特にディープラーニングの文脈においては厳しい制限があり、低い解像度で粗い3Dが再構成される傾向にあります。

点群
興味深い代替表現としては点群があります。ロボット工学からコンピュータグラフィックスまで幅広く使用されています。 柔軟性と計算効率は非常に高いものの、点と点を繋げる接続情報が不足しており、ほとんどの既存のアーキテクチャでは再構築可能なポイント数が少ないといわれています。

メッシュ
出力表現として頂点と面からなるメッシュもよく使われます。この表現は、ターゲットドメインからのテンプレートメッシュを必要としています。しかし、テンプレートメッシュを使用すると、作成されるモデルは、面や人体などの特定のドメインに制限されるので、椅子や車などの複数の物体カテゴリを同時に処理できるモデルを構築することは難しいとされています。または接続性など、3D出力に重要な特性を犠牲にしてしまう傾向もあり、自己交差と呼ばれるエラーを起こしたりなどもあります。

まとめると滑らかで正確な3D表現には以下の指標が必要になってきます。
任意のトポロジー(接続形態を点と線でモデル化したもの)と任意の解像度で表すことができる。
過剰なメモリ要件によって制限されない。
接続情報を保存できる。
特定のドメイン(オブジェクトクラスなど)に限定されていない
ディープラーニングテクニックとうまく融合するかどうかなど?
これらすべての要件を満たす新しい3D表現を見つけようというのが今回の論文の内容になります。
境界面として表現する
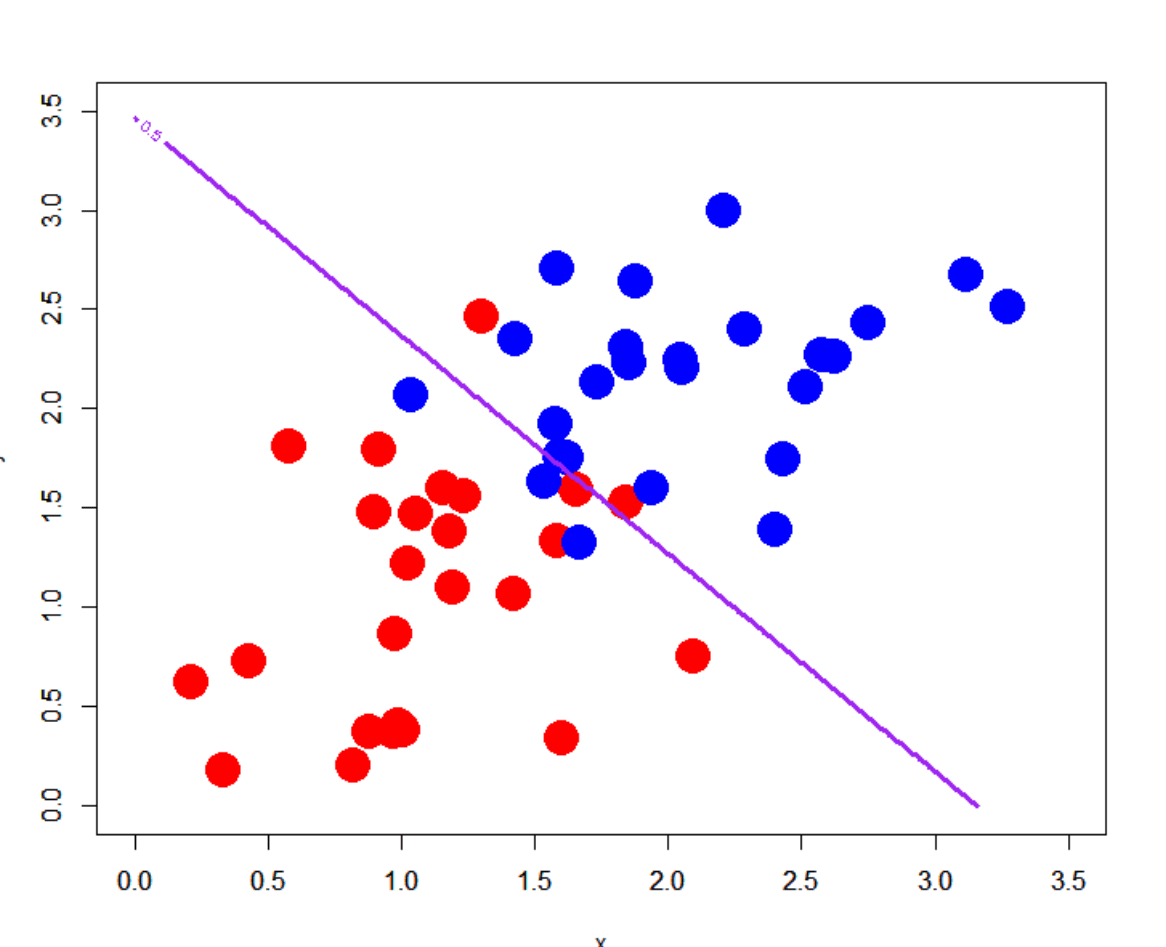
図1 決定境界
アイデアは単純なものです。3D物体を、オブジェクトの内側と外側を区別することを学習する分類器の決定境界として表します。
図1を見てわかる通り、決定境界とはニューラルネットワークの分類クラスの境目のことです。それぞれのクラスに正しく分類しているのが良い決定境界であり、機械学習アルゴリズムは良い決定境界を作るために学習しているともいえます。ニューラルネットワークの分類器の境界面を使って物体を表現することで、よりよい表現を得ることができ、連続的で滑らかな3D表現が得られます。
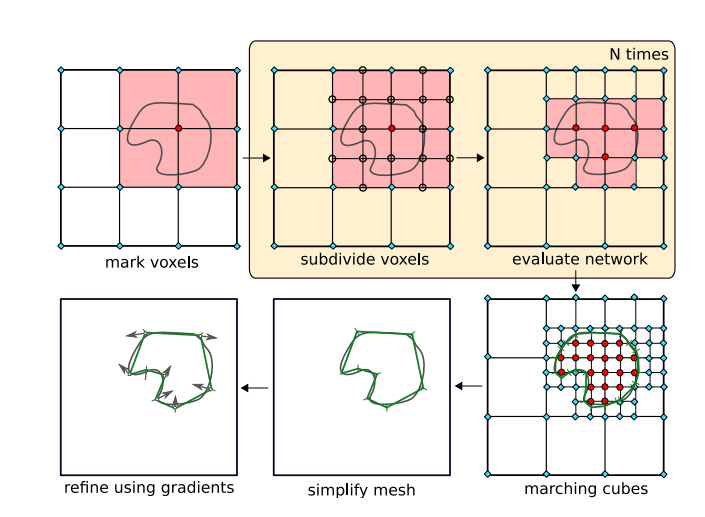
図2 推定手順
訓練には、真のクラスラベル(内側または外側)を知っている3D点をランダムにサンプリングしたものを使用します。
推論時には、入力として3D点を取り、その占有確率を出力することを目的とします。占有は、占有(赤丸)または未占有(ブルー丸)のどちらかとして評価されます。占有と未占有の両方を持つすべてのボクセルを特定し、それらをアクティブ(赤丸)としてマークし、またそれぞれ8つのサブボクセルに細分割します。(図2参照) 細分割によって出現した新しい格子点をそれぞれ占有(赤丸)または末占有(青丸)として評価しより境界を明確にしていきます。目的の出力解像度に達するまで、これらの手順を繰り返し、最後に得られた表現から、Marching Cubesアルゴリズムを用いて(各頂点の法線ベクトルを計算し)表面としてふさわしい点を見つけます。
結果
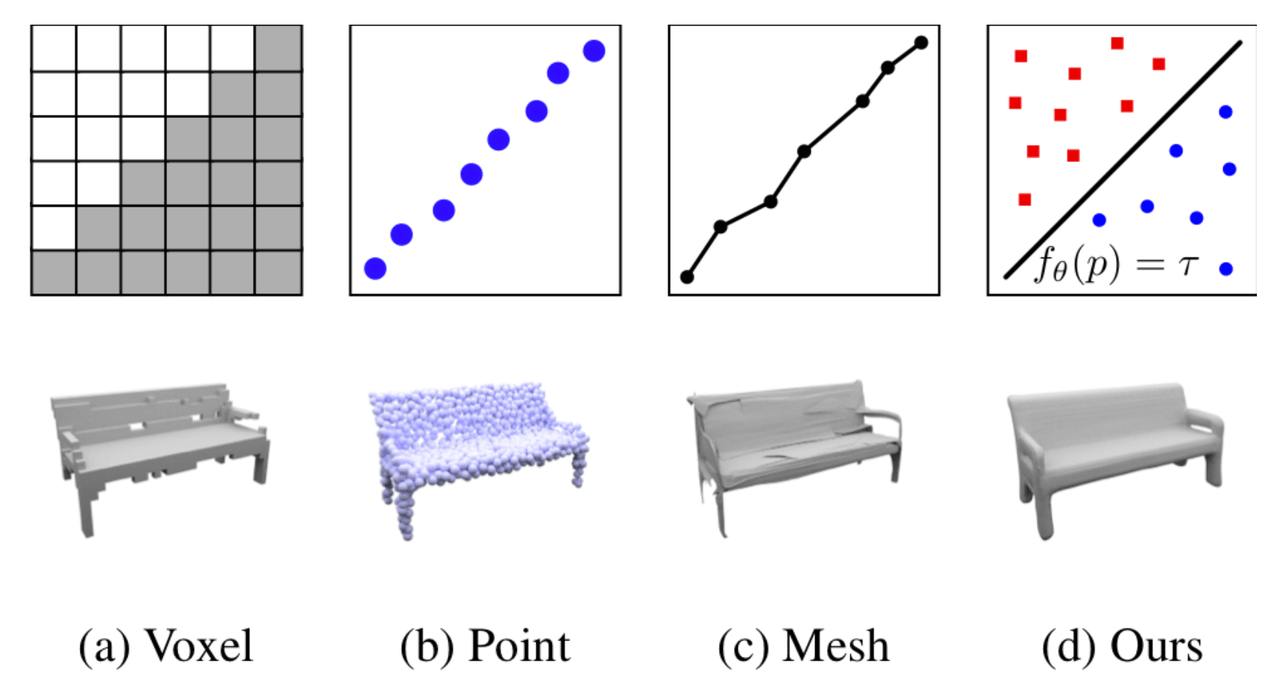
点群、単一画像、ボクセルグリッドからの3D再構成に関する広範な実験を行っています。詳細まで滑らかに表現できるため、既存の手法と比較して優れた結果が得られています。
非常に表現力があり、現実的な高解像度メッシュを表現するのに有効であることが分かりました。教師付き学習と教師なし学習の両方に効果的に使用できるそうで、非常に便利な表現法ではないでしょうか。


この記事に関するカテゴリー









