
How Should We Link Different Resolution Features? : D3Net Proposed By Sony
3 main points
✔️ Propose a mechanism D3 Block for tasks that require high-density estimation!
✔️ Solves aliasing problems caused by dilated convolution and skip connection!
✔️ Achieved SoTA on semantic segmentation and source separation tasks and showed generality of the model!
Densely connected multidilated convolutional networks for dense prediction tasks
written by Naoya Takahashi, Yuki Mitsufuji
(Submitted on 21 Nov 2020 (v1), last revised 9 Jun 2021 (this version, v2))
Comments: CVPR2021
Subjects: Computer Vision and Pattern Recognition (cs.CV); Machine Learning (cs.LG)
code:

The images used in this article are from the paper, the introductory slides, or were created based on them.
Introduction
D3Net is a network focused on high-density estimation tasks, i.e., tasks such as semantic segmentation and source separation that require estimation of the same dimensionality as the input image dimensionality. D3Net is a network focused on high-density estimation tasks, i.e., tasks such as semantic segmentation and source separation that require estimation of the same dimension as the input image dimension. Recently, there has been a lot of research on scaling up CNNs to approach ViT performance, mainly focusing on the convolution layer, such as changing the kernel size and employing Deformable Convolution to expand the receptive field. In this context, we propose a method for efficiently expanding the receptive field using dilatedconvolution. In particular, it handles high-density tasks and is designed to be very tightly connected, focusing on the importance of feature extraction at multiple resolutions, i.e., the compatibility of global and local features.
Major contributions include
- We proposed D2 Block, which combines skip-connection and dilated convolution, to address the importance of dense feature extraction at multiple resolutions.
- D2 Block incorporates multidilated convolution, solving the aliasing problem that occurs when dilated convolution is incorporated directly into DenseNet.
- We proposed D3 Block, which incorporates D2Block into a nested structure and flexibly extracts features at each resolution by performing multiple convolutions with different expansion ratios.
- Achieved SoTA on dense estimation tasks (semantic segmentation and source separation) for different domain tasks, demonstrating the generality of the proposed method
This paper is a bit old, but it is interesting because it focuses on aliasing the expansion convolution to improve accuracy. Let's take a look at D3Net.
High-density estimation task
Tasks that require the same output as the input dimension, such as semantic segmentation and noise source separation, require classification and regression at the pixel level. Therefore, both local features that identify detailed sites and signals and global features that capture the entire object are important.
Naturally, there is a dependency between global and local features. It is important to consider features of several different resolutions simultaneously, rather than features of a particular resolution.
However, existing approaches (FCN, UNet, HRNet, etc.) connect feature maps of different resolutions only a few times (see figure below). This paper addresses this issue and argues for the importance of densely modeling features of multiple resolutions simultaneously, and proposes D3Net.

big picture
D3Net is based on DenseNet, a popular CNN model, a very dense network of four layers of DenseBlocks with skip-connection between all layers within each block. skip-connection allows local features to be retained until later stages, maximizing the use of information while minimizing model size. This is the perfect motivation for this paper, as it allows us to densely connect various features. We propose D3 Block as a nested structure for more flexible modeling, and D3Net as a network composed of D3 Blocks.
Multidilated Convolution
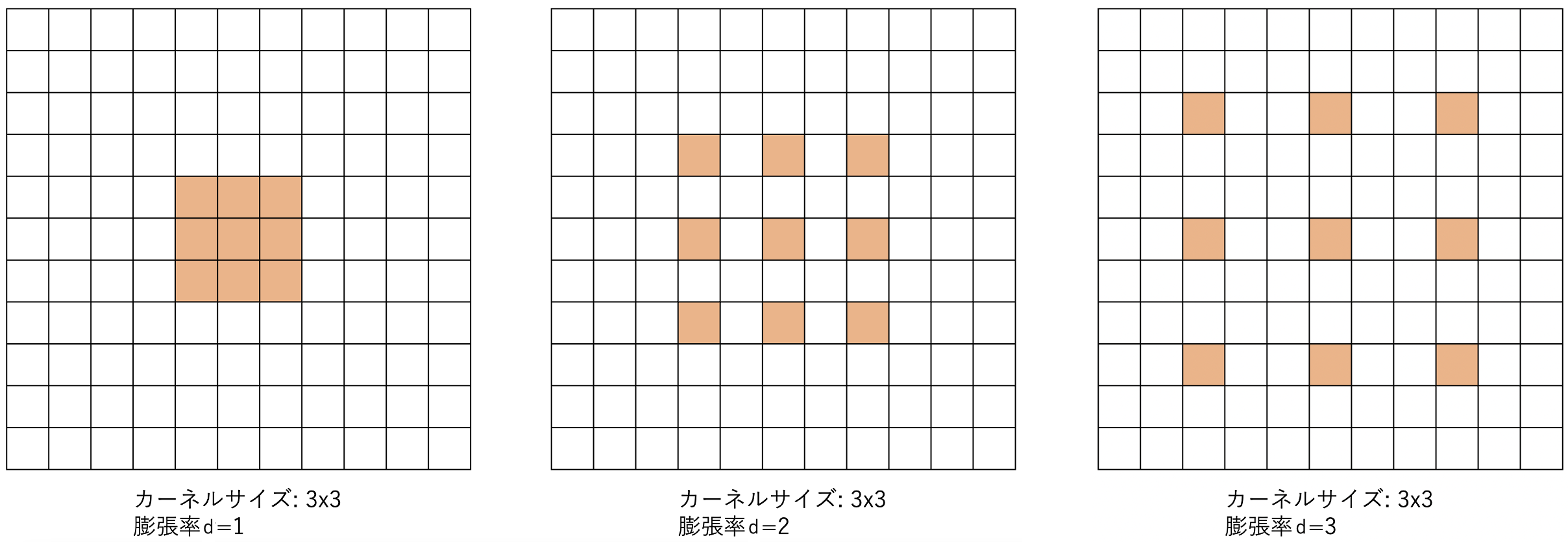
Let's start with the core element: expanding the receptive field of a CNN is an essential issue for large-scale and high-accuracy CNNs. The expansion of the receptive field enables long-range dependence and global features to be captured, which can be fully utilized for high-density estimation. In this paper, we focus on dilated convolution to efficiently expand the receptive field. As the name suggests, a wide range of features can be considered by dilating the kernel with the same number of parameters. The figure below shows an image. The receptive field is expanded by changing the sampling interval with the same number of parameters.
The use of dilated convolution can efficiently expand the receptive field, and in fact, a combination of DenseNet and dilated convolution has already been proposed. In this paper, we focus on the aliasing problem that occurs in this case and make improvements. This means that high frequencies above the Nyquist frequency can be indistinguishable from low frequencies, resulting in an aliasing problem.
Existing methods apply multiple standard convolution layers before dilated convolution to remove high-frequency components that cannot be processed uniquely, by making them take the role of low-pass filters. However, in the case of Skip-Connection as in DenseNet, such processing is not possible, and aliasing problems such as (a) in the figure below occur.
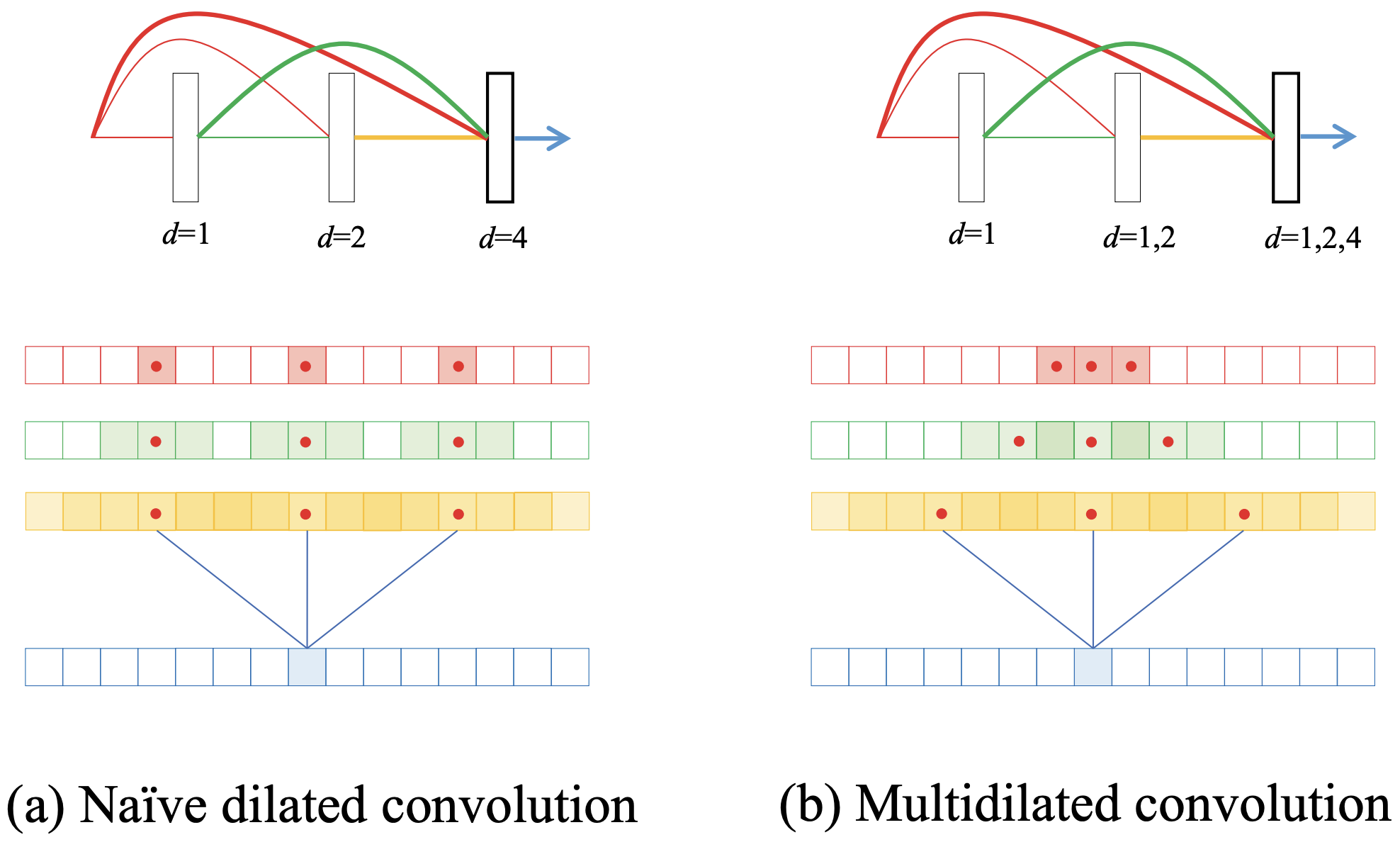
By doubling the expansion rate d, the receptive field is expanded exponentially. For simplicity, we can grasp the aliasing problem by expressing the sampling for the feature map in one dimension. If there are no blind spots in the feature map sampling, aliasing will not occur. the third layer of dilated convolution (d=4) is connected to the feature maps from all previous layers by skip-connection. Here, sampling each map at d=4 (red dots) allows us to see the blind spots in the receptive field. Since the red map is the input itself, the receptive field is only at the sampled point (red square), where the aliasing problem is most pronounced. Then consider the sampling of the green map processed with d=1, i.e. the usual 3x3 convolution: by sampling one square we can indirectly take into account 3x3 squares (green squares), but we can still see that there are blind spots in the receptive field. Since there are no blind spots in the previous yellow map, at first glance, it appears that there is no effect if we continue to increase d. However, D3Net will never increase d. However, D3Net does not continue to increase d. Instead, it resets d to 1 again block by block, and repeats dilated convolution over and over again. This is because it is important to densely repeat high- and low-resolution feature extraction. In other words, this would result in an unstable model with significant aliasing problems in each block.
The proposed method (see (b) above) solves the aliasing problem by using multiple expansion rates. There is nothing difficult about it; it simply samples each map with the maximum expansion ratio that does not cause aliasing, such as d=2 for a feature map with d=1 and d=4 for a map with d=2. This solves the aliasing problem while allowing convolution at multiple resolutions in a single layer. the third layer convolution shows that the feature map is compatible with a local feature map densely extracted at d=1 to a feature map that becomes global at d=1, d=2, and d=4, in that order. The equation is expressed as follows. l is the current layer and x is the feature map. 0 to l-1 feature maps are obtained by skip-connection, and Batch Normalization and ReLU are applied (ψ in Eq.) In contrast, conventional dilated convolution simply applies a filter for each layer. In contrast, multidilated convolution applies a different dilatation di and filter for each i, which represents which dilatation d is skip-connected from the convolution.
![]()
![\begin{align*}
x_l = \sum_{i=0}^{l-1}\psi([x_0,x_1,\cdots,x_{l-1}])\;\circledast_{d_i}\;w_l^i
\end{align*}](https://texclip.marutank.net/render.php/texclip20230113154150.png?s=%5Cbegin%7Balign*%7D%0A%20%20x_l%20%3D%20%5Csum_%7Bi%3D0%7D%5E%7Bl-1%7D%5Cpsi(%5Bx_0%2Cx_1%2C%5Ccdots%2Cx_%7Bl-1%7D%5D)%5C%3B%5Ccircledast_%7Bd_i%7D%5C%3Bw_l%5Ei%0A%5Cend%7Balign*%7D&f=c&r=300&m=p&b=f&k=f)
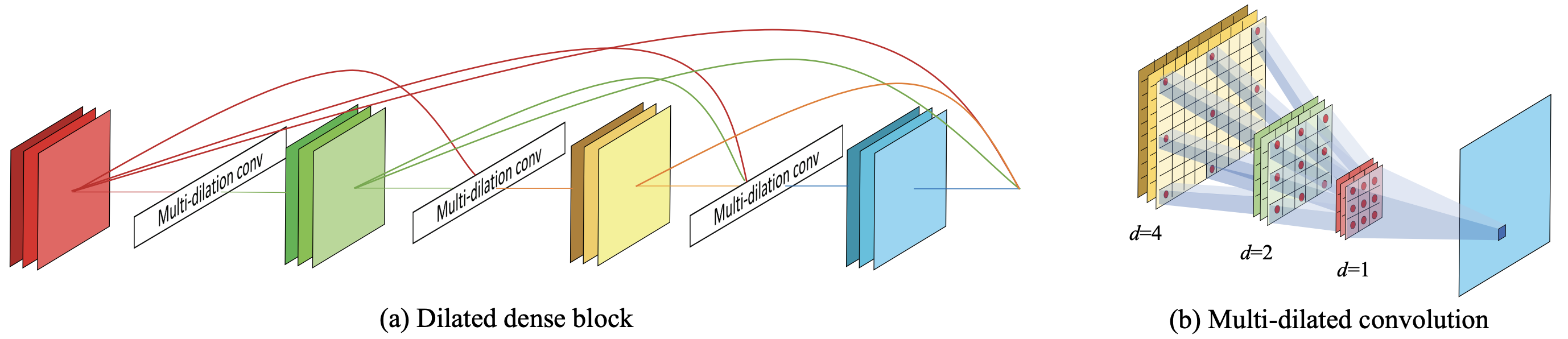
The block connecting multiple multidilated convolutions is called the D2 Block and is proposed as the core block of the D3 Block. the D2 Block can thus avoid aliasing and simultaneously model information of various resolutions in an exponentially expanding receptive field. simultaneously in an exponentially expanding receptive field, thus avoiding aliasing.
Finally, an overview diagram of the D2 Block is shown below. This is a two-dimensional example of the diagram shown above.
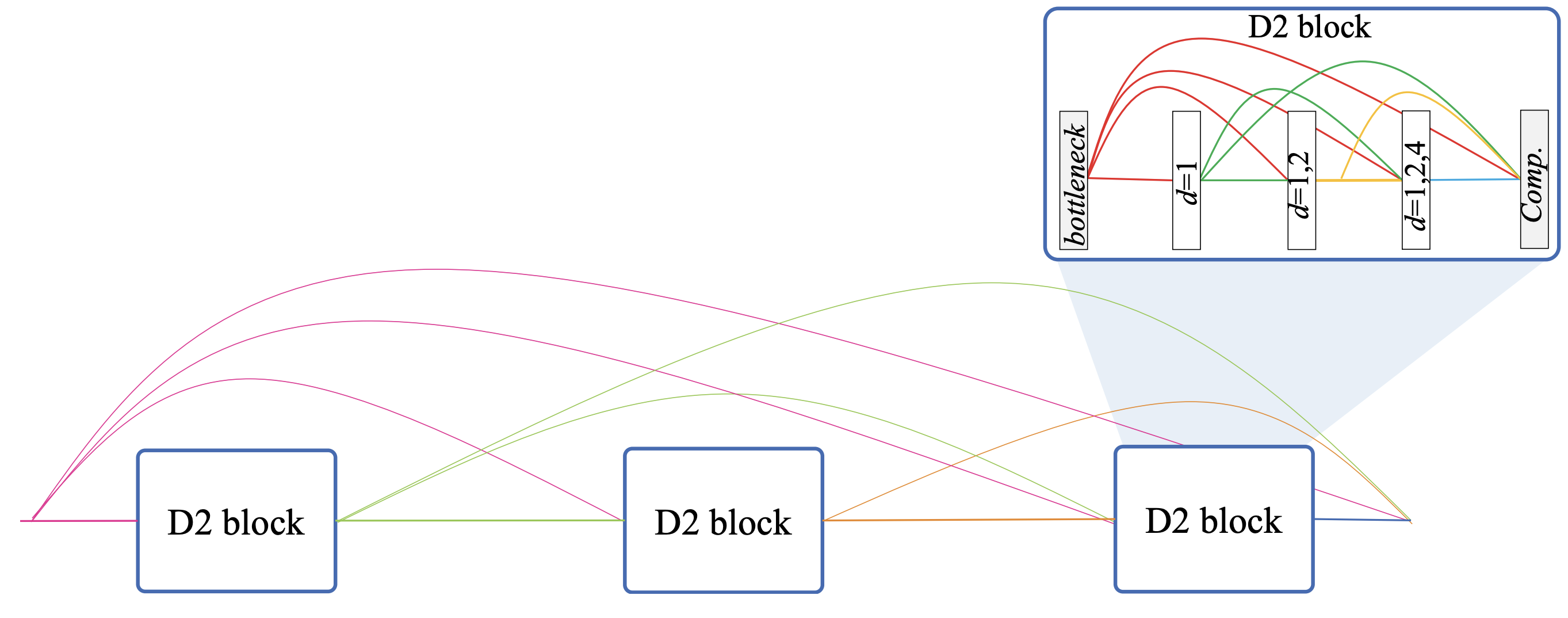
D3 Block
The D3 Block has the structure shown in the following figure. First, let us suppress the details of the D2 Block. The growth rate is k.
Growth rate k
As mentioned earlier, D3Net is based on DenseNet, which, unlike ResNet's mechanism of simply increasing the number of channels by convolution, branches off from the main n feature maps and adds k-generated feature maps to the main one (n+k). Therefore, this k is called the growth rate; in the D2 Block formula, each x0,x1,... x1,..., xl has k maps. However, n+k is not the exact number of channels, since D2 Block has a Bottleneck layer and a Comp layer before and after, and performs channel compression.
Also, up to this point, we have considered multiple resolutions with multidilated convolution, but no downsampling is performed, so the feature maps are all the same size.
nest structure
The D3 Block is composed of M D2 Blocks. As can be seen in the figure, the D3 Block has a skip-connection nested structure, just like the D2 Block, which has skip-connected all layers of the multidilated convolution. Skip-connection is applied to all blocks of the D2 Block. In other words, the structure is designed to be closely skip-connected both between and within blocks. This makes the D3 Block an extremely dense and flexible model since a given D2 Block interprets features that have already considered information at multiple resolutions in the previous D2 Block at multiple resolutions.
hyperparameter
The D3 Block has five parameters (M, L,k, B,c). As mentioned earlier, M is the number of D2 Blocks, L is the number of layers of multidilated convolution in the D2 Block, k is the growth rate, B is the number of channels in the bottleneck layer, and in this paper we set B=4k. The last c is the compression ratio of the Comp layer, which compresses the number of channels by a factor of c.
D3Net
D3Net refers to any model that employs D3 Block, but this paper uses an improved model based on DenseNet. Although no downsampling has been done so far, D3Net, like DenseNet, performs channel count changes and downsampling at the Transition layer. This will allow the next D3 Block to perform feature extraction at different map sizes and multiple resolutions.
experiment
Experiments demonstrate the generality of the proposed method to the task domain by validating it on two tasks that require high-density estimation.
semantic segmentation
The focus is on evaluating D3Net as a backbone. The dataset used is CityScapes, a dataset consisting of 5000 images of car fronts-capes in 50 cities. In each image, the corresponding object class is annotated at the pixel level as follows The evaluation is the average mIoU of IoU per class for the 19 classes.
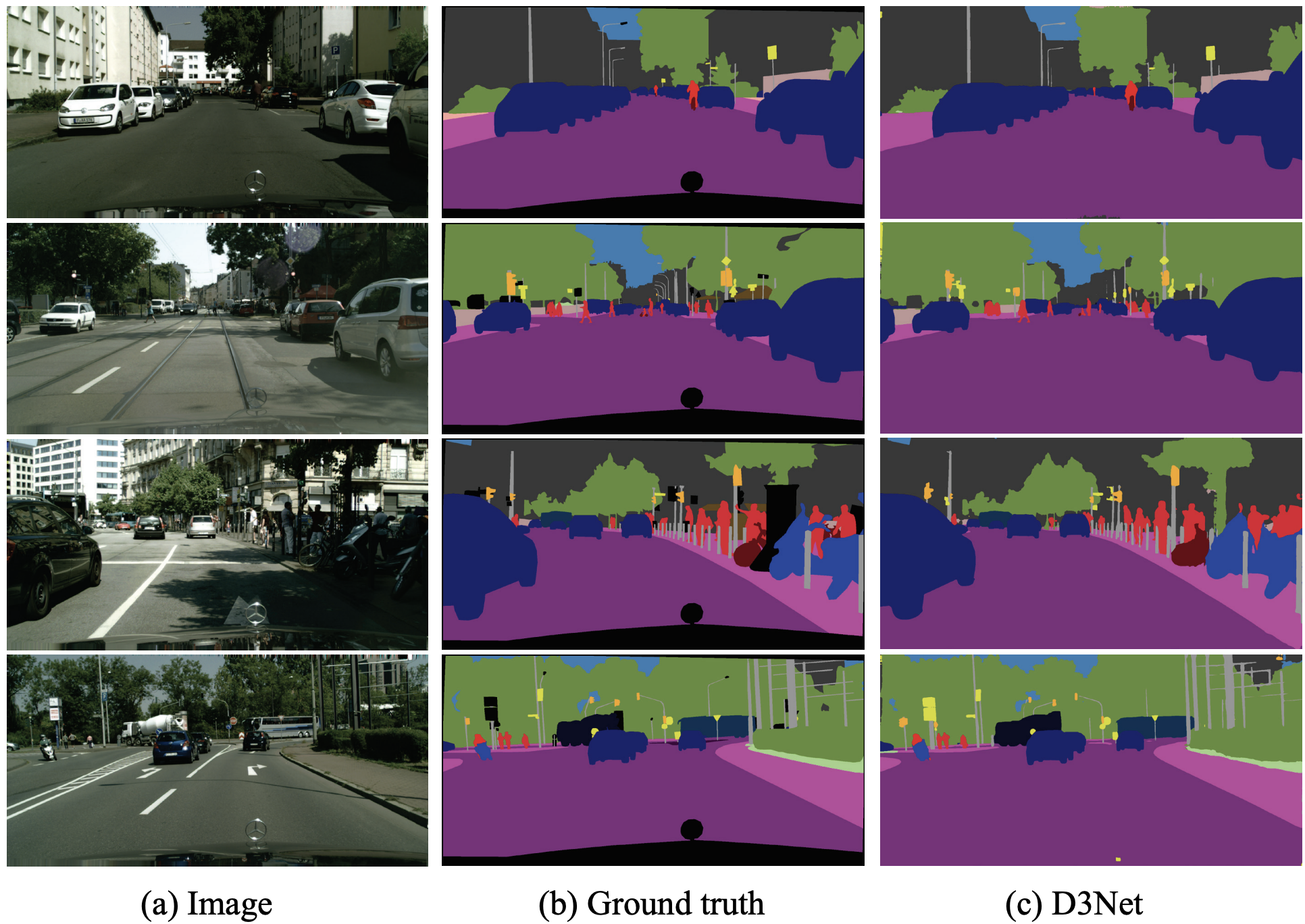
architecture
D3Net assumes two models: D3Net-S has (M,L,k,c)=(4,8,36,0.2) and the number of output channels in each D3 Block is (32,40,64,128); D3Net-L has (M,L,k,c)=(32,48,96,192).
result
To show the effectiveness of multidilated convolution (D2 Block), we also trained with standard convolution (without dilation) and standard dilation (standard dilation). To demonstrate the effectiveness of D3 Block, DenseNet-133 and DenseNet-189 with a similar number of parameters are also prepared and compared with DenseBlock.
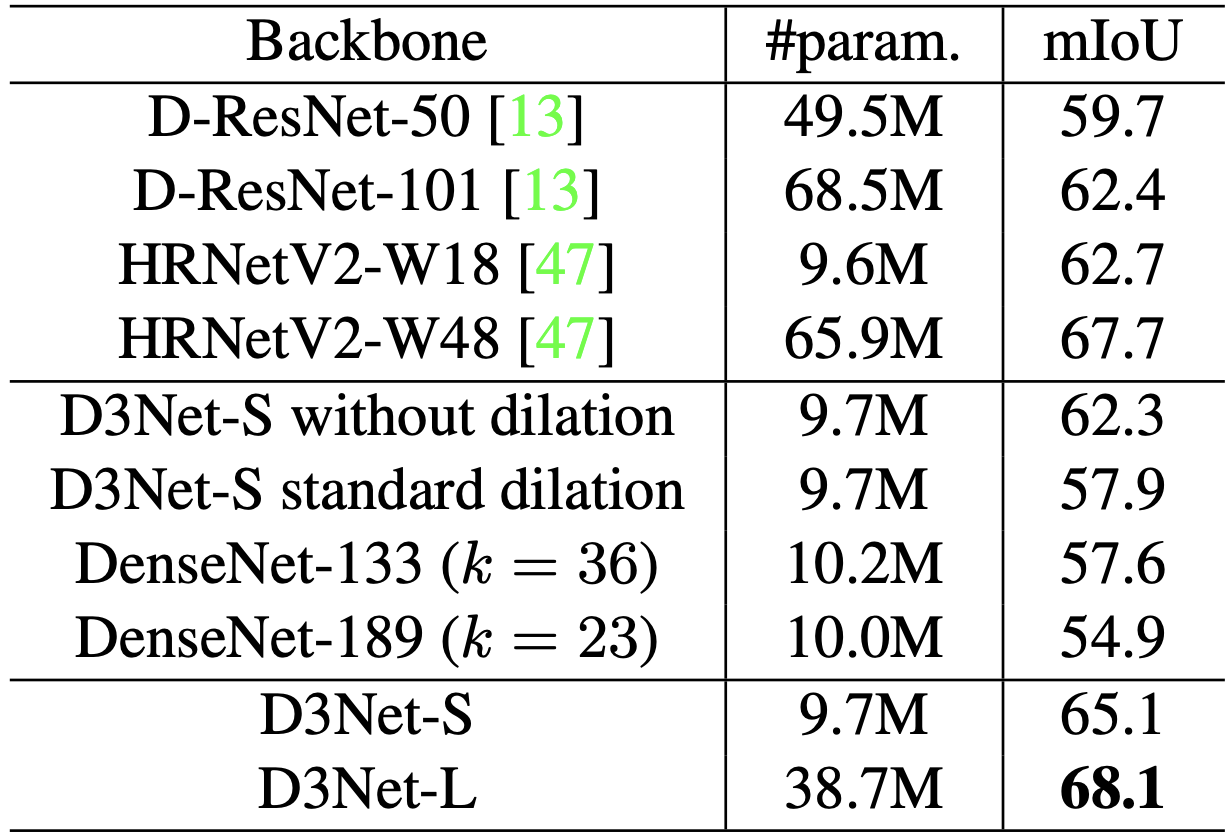
D3Net-S performed significantly better than WITHOUT dilation and STANDARD dilation, improving mIoU. Interestingly, standard dilation also showed lower accuracy than without dilation. This may be due to aliasing issues. The proposed method avoids aliasing and successfully improves accuracy. It also achieves higher accuracy for DenseNet, which has a similar size to D3Net, showing the effectiveness of D3Net in increasing the receptive field by dilated conv and allowing a higher k due to the efficient number of parameters.
D3Net-L achieved the highest accuracy over all baselines with fewer parameterizes than the SoTA model HRNetV2W48 at the time of publication.
Next is a comparison with the SoTA model, only D3Net-L has more training times to keep the model scale fair.
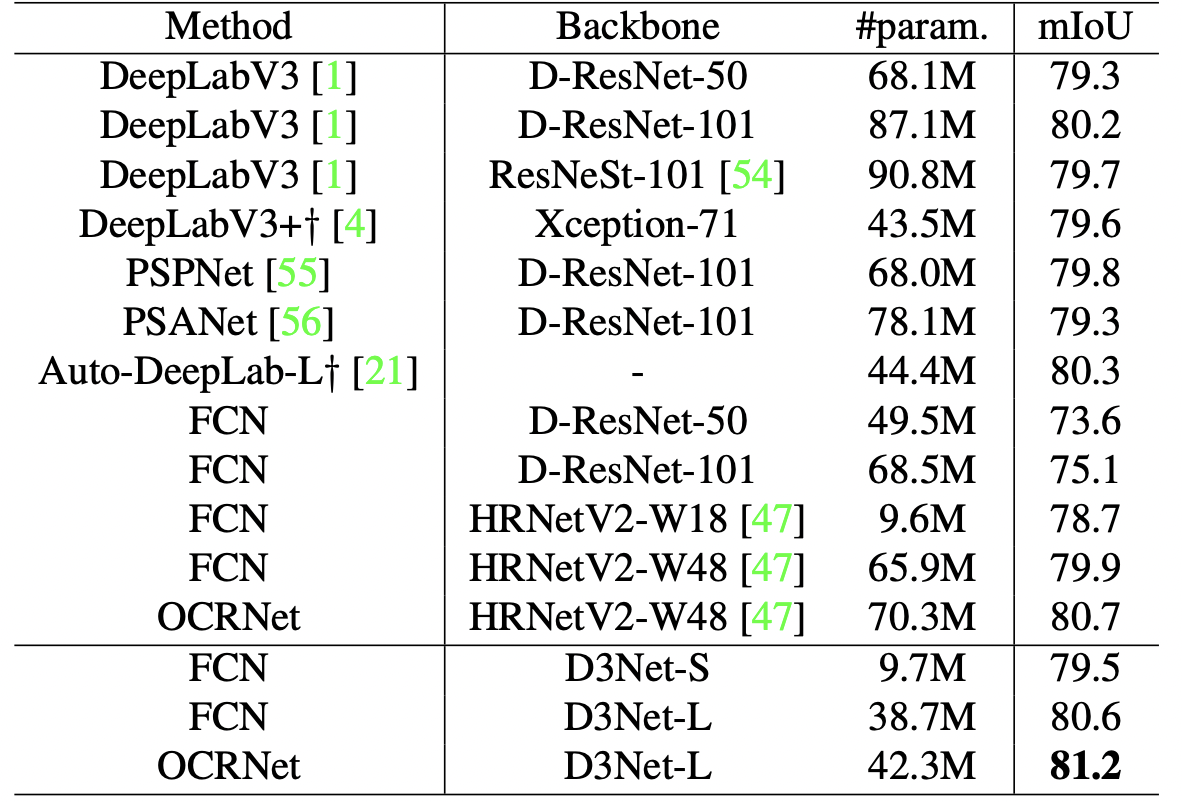
There are two methods: a DCN-based method and an OCRNet-based method, and in the FCN-based method, D3Net-L outperformed all baselines with far fewer parameters than HRNetV2p-W48, D-ResNet-101, and DResnet-50. D3Net-L performed even better, achieving 81.2% accuracy, the highest accuracy at the time of publication.
sound source separation
Sound Source Separation is the task of separating an audio signal into its sound sources. For the MUSDB18 dataset used in this paper, the goal is to separate the sound sources of approximately 10 hours and 150 songs into four sound sources: Bass, Drums, Vocals, and Other.
evaluation
Many methods use the short-time Fourier transform (STFT) to transform time-domain signals into frequency information in time window units and treat them as images. In other words, this task is similar to the segmentation task, which is to estimate the amplitude of each source for a two-dimensional STFT map. It differs from segmentation in some ways. It differs from segmentation in several ways: it is a regression problem to estimate amplitude, not just classification; unlike images, which only show the front object closest to the camera, speech signals are complex superpositions of multiple sources; and STFTs do not have global invariance concerning frequency.
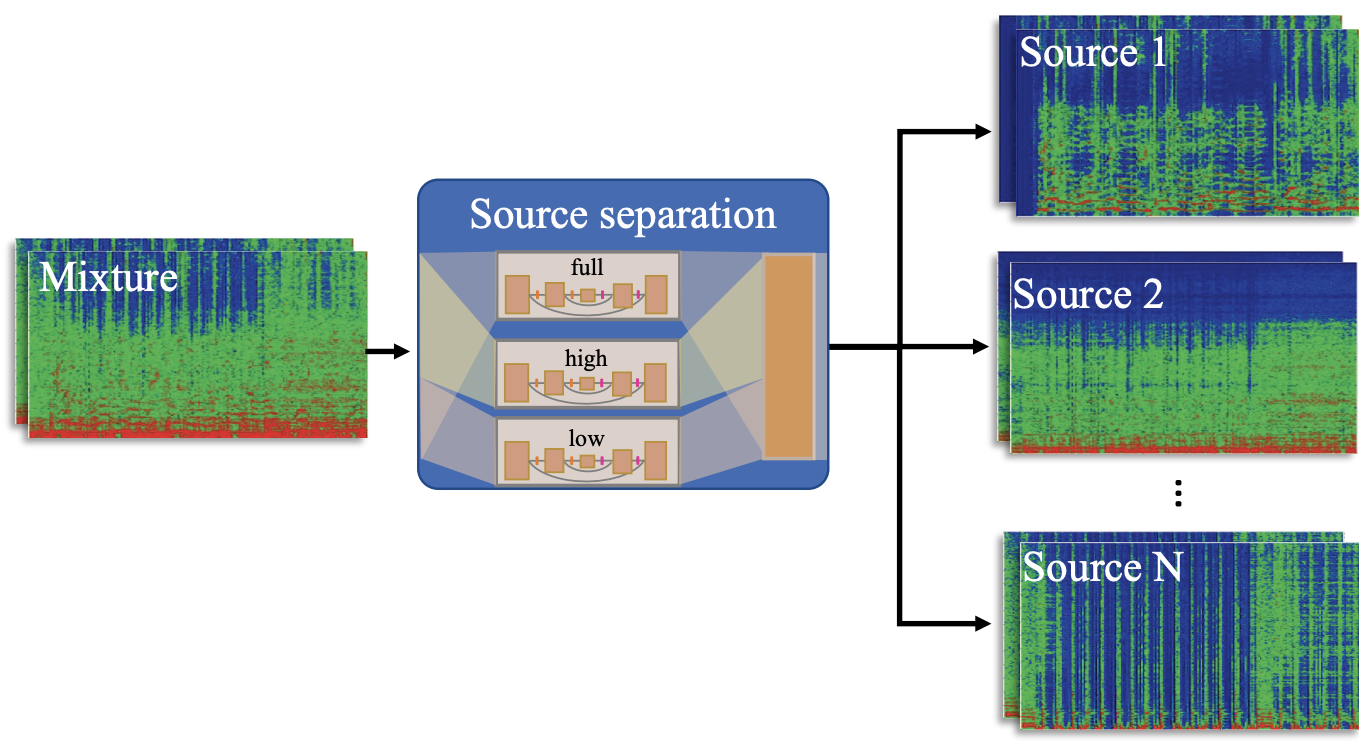
architecture
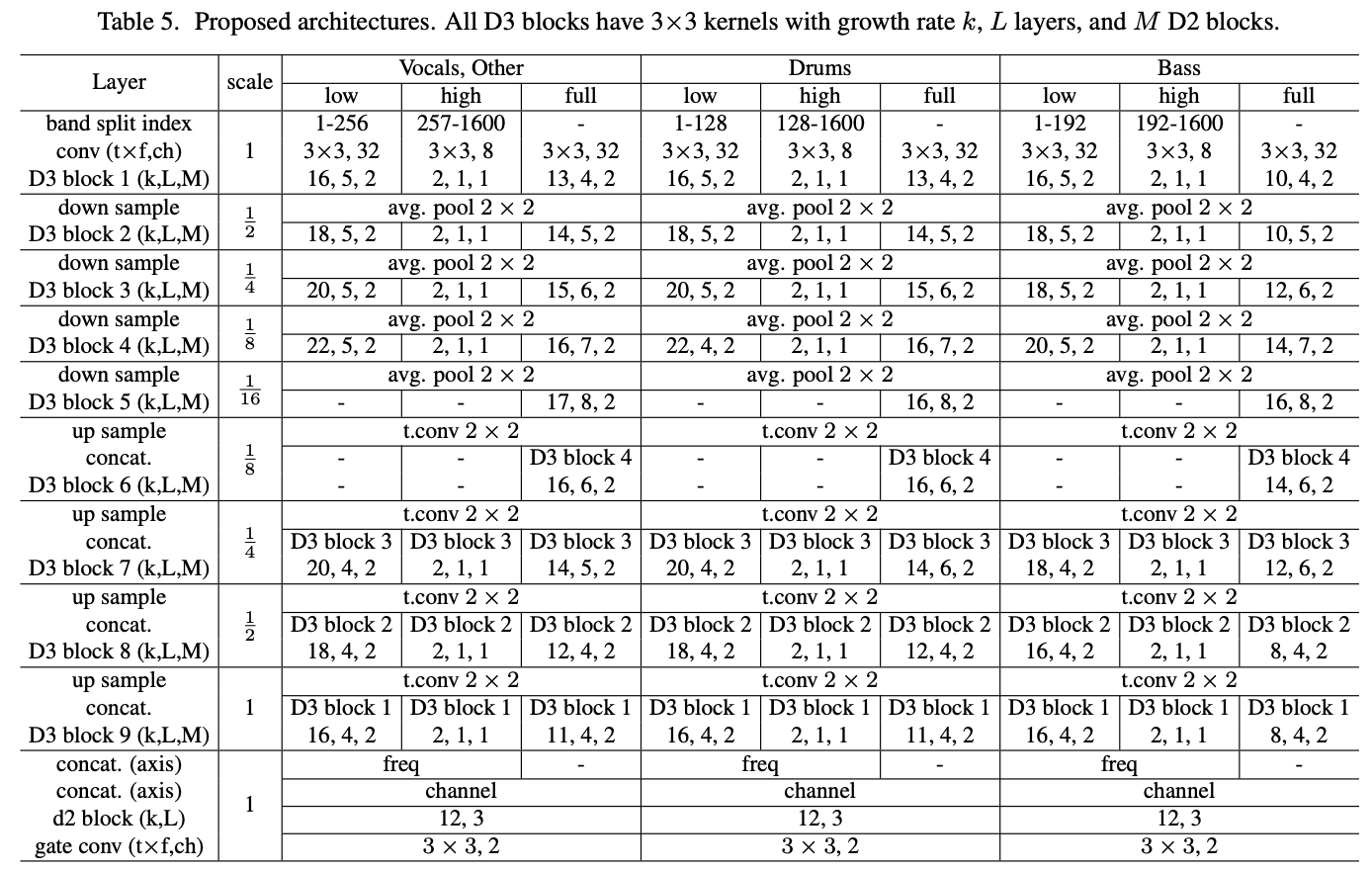
D3Net prepares a network for each of the four sources and trains and estimates the spectrogram. The output of the network is MSE for loss. The output of the network is the MSE for the loss, and the frequency bands are trained separately for low, high, and full according to the best model. In other words, D3Net uses a total of 12 networks trained on 3 bands for each of the 4 sources. The output of the networks is used in a commonly used frequency domain source separation method called multichannel Wiener filter (WMF) to obtain the final separation result. The details of the model are shown in the table below.
result
The signal-to-distribution ratios (SDR) of the proposed method and the SoTA model are shown. D3Net showed the highest accuracy for vocals, drums, and accompaniment (Acco), where Acco is the sum of drums, bass, and Other. The average SDR for the four instruments was 6.01 dB, which is better than all the bass lines, including the SoTA models such as TAK1 and UHL2.
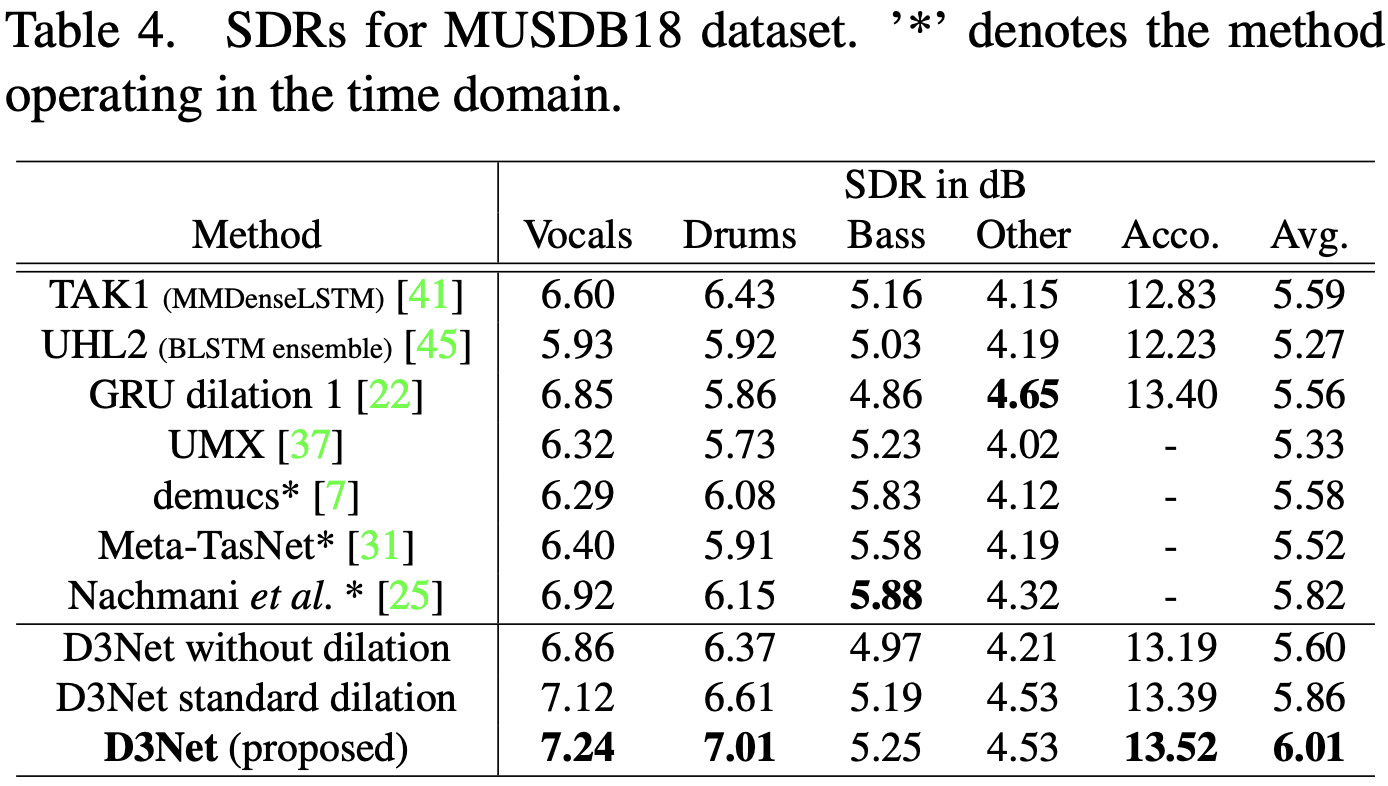 The effectiveness of D3 Block, which employs multidilated conv and its nested structure, is evident for TAK1, which uses LSTM to expand the receptive field. Also, GRU dilaltion1 is composed of dilated conv and dilated GRU units without using up-sampling or down-sampling, indicating the effectiveness of D3Net for dense processing at multiple resolutions.
The effectiveness of D3 Block, which employs multidilated conv and its nested structure, is evident for TAK1, which uses LSTM to expand the receptive field. Also, GRU dilaltion1 is composed of dilated conv and dilated GRU units without using up-sampling or down-sampling, indicating the effectiveness of D3Net for dense processing at multiple resolutions.
For bass, D3Net could not outperform existing methods because time-domain methods are easier to recover. However, D3Net is the best-performing frequency-domain method.
Standard dilation performed better than WITHOUT dilation for source separation ablation. In any case, the multidilated conv of the proposed method significantly outperforms standard convolution and standard dilated conv, a result that demonstrates the importance of handling the aliasing problem.
impression
I was wondering how the dilated conv would be affected by the blind spots in between, but it was a good insight because I had not thought of solving it in terms of aliasing.
By the way, there is Deformable Convolution (Deformable Convolution) which is more flexible and dynamic sampling than dilated conv, but I am wondering how aliasing affects it here. InternImage, introduced previously, uses DCNv3 as a strategy to bring performance closer to ViT, but I would like to investigate whether aliasing issues arise.
summary
In this study, we demonstrated the importance of learning multiple resolutions densely for high-density estimation tasks and proposed D3Net. It works accurately in the high-density estimation task by combining and nesting dense skip connections while solving the aliasing problem that occurs in standard dilated conv.
Experiments on semantic segmentation and source separation demonstrate the effectiveness and generality of the proposed method in different tasks and domains, outperforming the state-of-the-art backbone with a small number of parameters.
The paper claims to show important insights into the frequency of tightly coupling local and global information at multiple resolutions when designing CNNs. We look forward to future developments.
Categories related to this article





