SSSD Model Applying A Diffusion Model To The Missing Completion Problem For Time Series Data

3 main points
✔️ Applying a diffusion model and a structured state-space model to complement missing time-series data, a key issue in practical applications
✔️ The model greatly improves on the poor performance of previous completion algorithms depending on the faulty scenario
✔️ The same mechanism is applied to the time-series prediction problem

Diffusion-based Time Series Imputation and Forecasting with Structured State Space Models
written by Juan Miguel Lopez Alcaraz, Nils Strodthoff
(Submitted on 19 Aug 2022)
Comments: Published on arxiv.
Subjects: Machine Learning (cs.LG); Machine Learning (stat.ML)

code：  

The images used in this article are from the paper, the introductory slides, or were created based on them.

summary

This paper proposes a new method for the completion of missing values in time series data: the diffusion model, made famous by its use in DALL-E2, Stable Diffusion, etc., is applied here to time series data rather than images. In many real-world data analysis tasks, missing value completion is often required. In this paper, we propose SSSD, a completion model based on two novel techniques: a state-of-the-art generative model, the (conditional) diffusion model, and an internal model structured state-space model, which is particularly suited to capture long-term dependencies in time series data. We demonstrate that SSSD outputs probabilistic attribution and forecasting performance that rivals or exceeds the state-of-the-art on a wide range of challenging data sets, including pause-missing scenarios that failed to provide meaningful results, and on a variety of missing scenarios.

Introduction

There are many reasons for missing input data, including poor data entry, equipment failure, and lost files. Dealing with missing input data is a significant challenge in machine learning applications because most algorithms require data without missing values to learn. Unfortunately, as demonstrated in previous studies, the quality of data completion can have a significant impact on downstream tasks, and inadequate completion can even bias downstream analyses, thus calling into question the validity of the resulting results.

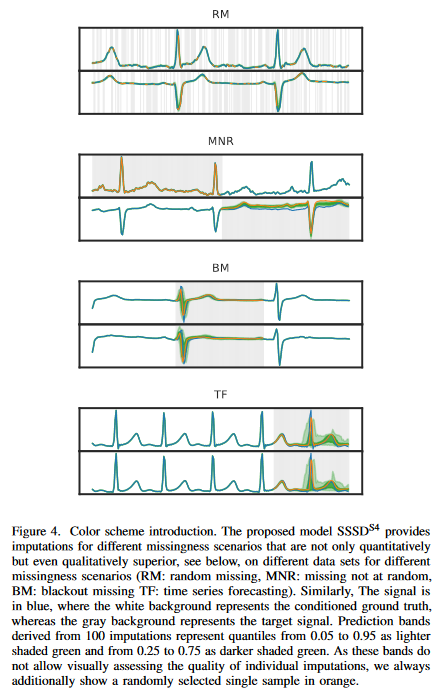
This study focuses on time series data. We then consider various missing scenarios (Fig. 4): RM: random missing, MNR: non-random missing, BM: pause missing, and TF: time series forecasting. Thus, time series prediction can be regarded as one of the cases of pause missing and can be discussed in a unified way if the location of the completion window is at the end of the sequence. We also emphasize that the most realistic scenario for dealing with completion as an unspecified problem class is the use of stochastic completion methods. This permits a sample of various plausible completions rather than providing only a single completion. Thus, we can examine the sensitivity of downstream algorithms to the completion portion, which represents one of the foundations of perturbation-based explainable AI methods. Finally, the breadth of the prediction interval provides a way to quantify the inherent uncertainty in the data.

There is a vast literature on time series completion, ranging from statistical methods to autoregressive models. Recently, deep generative models have begun to emerge as a promising paradigm for modeling time series completion in long sequences and time series prediction problems in long horizons. However, many existing models are limited to random missing scenarios or exhibit unstable behavior during training. In some datasets, even state-of-the-art approaches have failed to provide even qualitatively meaningful completions in pause-missing scenarios.

This study aims to address these shortcomings by proposing a novel generative model-based approach for complementing time series. The paper uses diffusion models, more specifically the DiffWave framework proposed in the context of speech generation, as the current state-of-the-art in terms of generative modeling in different data modalities. The second main element is the use of structured state-space models instead of extended convolution or transformer layers as the main computational building blocks of the model, which is particularly suitable for handling long-term dependencies in time series data.

In summary, the main contributions of this paper are

STRUCTURED STATE SPACE DIFFUSION (SSSD) model for time series completion

time-series complement

As with time series data, let _x0 be a data sample with the shape of ^RL×K where L is the number of time steps and K is the number of features or channels. A binary mask that matches the shape of the input data, i.e., mimp _∈ [0, 1] ^L×K, is commonly used, where the conditional value is 1 and 0 represents the value to be complimented. If there are missing values in the input, an additional mask _{mmvi of} the same shape is needed to distinguish between values that are present in the input data (1) and values that are not present (0).

We restate the different missing scenarios defined in the literature, although we classify them separately. We define random missing (RM) as the situation where zero entries in the imputation mask are randomly sampled according to a uniform distribution over all channels of the entire input sample. Next, Missing Not at random (MNR) assumes a random subset of xi missing at x0 in the L dimension of each K. Finally, blackout missing (BM) assumes that there is a missing subset of xi in x0 of the L dimensions for all K. As mentioned earlier, time series forecasting (TF) is a special case of BM completion, where the completion domain spans a continuous domain of t time steps. The signal color is blue, with a white background representing the conditional ground truth and a gray background representing the target signal. The prediction bands resulting from the completion represent the 0.05 to 0.95 quantile in light green and the 0.25 to 0.75 quantile in dark green. Since these bands do not allow a visual assessment of the quality of individual completions, a single completion sample, always randomly selected here, is additionally displayed in orange.

diffusion model

Diffusion models are a type of generative model that has shown state-of-the-art performance in a variety of data modalities, from images to audio and video data. Diffusion models learn to map from the latent space to the signal space by sequentially learning to remove noise that is Markovianly added successively in the so-called forward process and released in the inverse process. These two processes are therefore the backbone of the diffusion model. The forward process is parameterized as follows

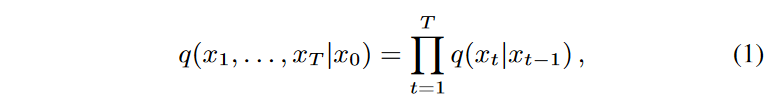
where q(xt|xt-1) = N (xt; √1 - βtxt-1, βt1) and the variance βt of the (fixed or learnable) forward process is the noise level adjustment. Equivalently, xt can be expressed in closed form as xt = √αtx0 + (1-αt) for ∼N (0, 1), where αt = ∑t i=1(1 - βt).

The inverse process is parameterized as follows

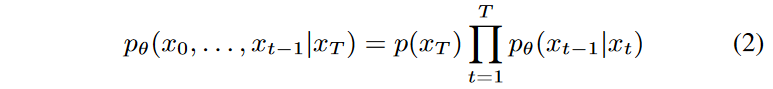
where _xT ∼ N (0, 1). Again, pθ(xt-1|xt) is assumed to be a normal distribution (with diagonal covariance matrix) with learnable parameters; Ho et al. showed that with a particular parameterization of pθ(xt-1|xt), the inverse can be learned with the following objective

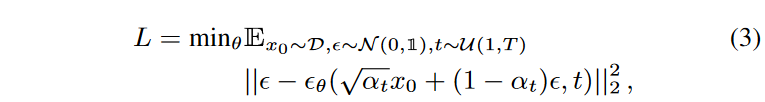
where D refers to the data distribution and θ(xt, t) is parameterized using a neural network. The objective can be viewed as a weighted variational limit of the negative log-likelihood, which reduces the importance of terms when t is small, i.e. when the noise level is small.

Extending the unconditional diffusion process described so far, we can consider a conditional deformation in which the inverse process is conditioned on additional information, namely θ = θ(xt, t, c). Here, the exact nature of the conditional information c depends on the application at the time and ranges from global labels to spectrograms. Here, it is given by the concatenation of the input (masked according to the completion mask) and the completion mask itself, i.e., c = Concat(x0 ( _{mimp mmvi}), (_mimpmmvi)). (where represent pointwise multiplication). In this study, we will consider two different setups (denoted D0 and D1, respectively), one in which the diffusion process is applied to the entire signal and the other in which it is applied only to the complementary region. In any case, the evaluation of the loss function in equation (3) is assumed to be performed only on input values for which ground truth is available, i.e.,_mmvi = 1. In D0, this is the reconstruction loss for input values corresponding to the nonzero portion of the (conditionally available) completion mask and the input token for which the completion mask vanishes In D1, the reconstruction loss vanishes by construction.

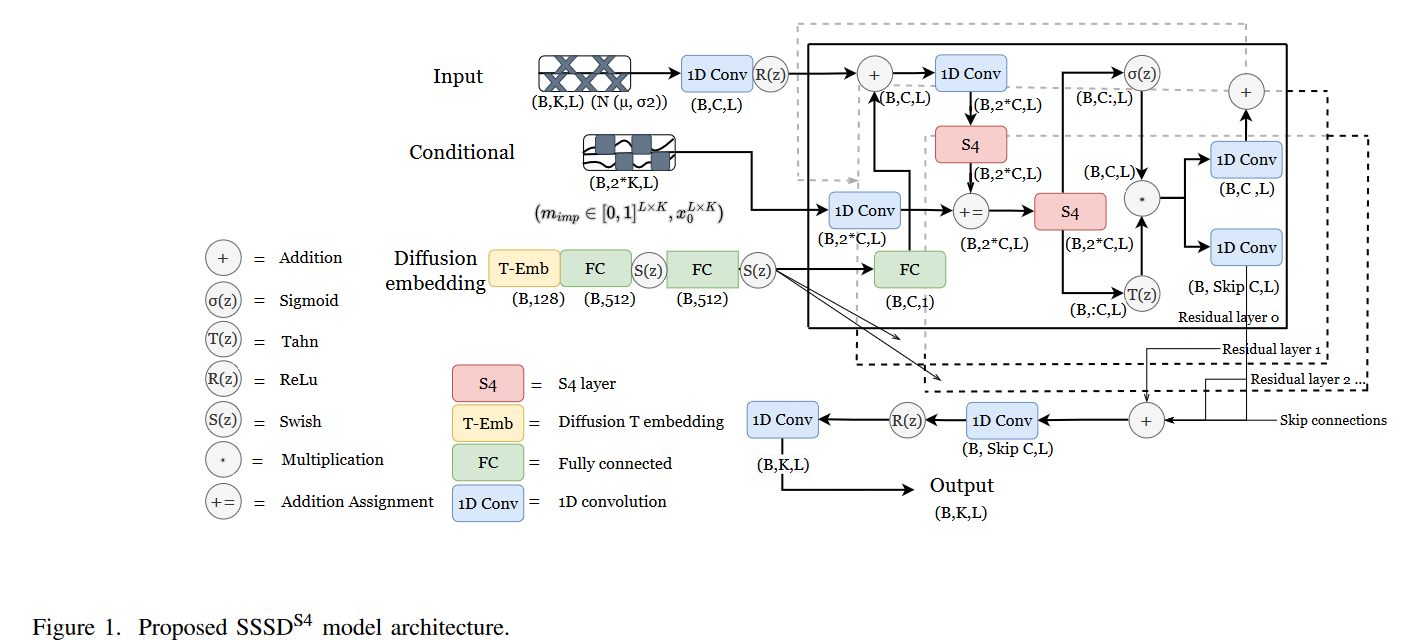
Like Tashiro et al. the authors perform a parameterization of θ(xt, t, c) based on the DiffWave architecture; unlike Tashiro et al. we do not deal here with an extended 4D internal representation of the shape (batch dimension, diffusion dimension, input channel dimension, time dimension). This is because many modern architectures for sequential data, such as transformers and structured state-space models discussed below, can only process sequential, i.e., 3D input batches, and thus require alternating processing of the time dimension and feature dimension. Here, we take the more conceptually simple approach of mapping the input channels to the diffusion dimension and only diffusing along the time dimension. That is, we process batches of shapes in (batch dimension, diffusion dimension, and time dimension). In addition, we modify the internals of the DiffWave architecture by using the S4 layer, which is better suited for processing time series data than the extended convolution used in the original architecture.

state-space model

The recently introduced structured state-space model (SSM) represents a very promising modeling paradigm, especially for capturing long-term dependence in time series. The core of this formulation is a linear state-space transition equation that connects a one-dimensional input series u(t) to a one-dimensional output series y(t) via an N-dimensional hidden state x(t). This transition equation is expressed 

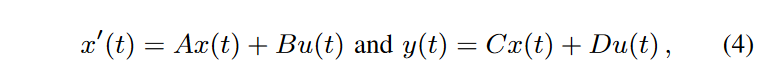
where A, B, C, and D are transition matrices. After discretization, the input-output relationship can be written as a convolution operation, which can be efficiently evaluated on modern GPUs. The ability to capture long-term dependencies relates to a specific initialization of A ∈ ^RN×N according to HiPPO theory. The Structured State Space Model(SSM)proposes a Structured State Space Sequence Model (S4) by stacking multiple copies of the above SSM block with appropriate normalization layers and point-order fully connected layers in the style of transformer layers and has demonstrated excellent performance on a variety of sequence classification tasks The S4 layer has demonstrated excellent performance in a variety of sequence classification tasks. Indeed, the resulting S4 layer can be used (with appropriate padding) as a drop-in replacement for the transformer layer, RNN layer, and 1D convolutional layer to parameterize the shape-preserving mapping between data and shape (batch, model dimension, and length dimension). based on the S4 layer, U net-inspired configuration, resulting from the combination of S4 layers, a generative model architecture for sequence generation, SaShiMi, has been presented. Although the model was proposed as an autoregressive model, the authors point out that it is already possible to use (non-causal) SaShiMi as a component of state-of-the-art non-autoregressive models such as DiffWave.

Proposed Method

The authors propose three different variants of the Diffwave-based diffusion model. First, we proposed ^SSSDS4, a conditional DiffWave-variant, which replaces and fits the S4 layer as a diffusion layer within each of its residual blocks after adding the diffusion embedding, instead of a two-way extended convolution. As a second modification, we include a second S4 layer after the additive assignment with the conditional information, giving the model additional flexibility after combining the processed input and the conditional information. This architecture is shown schematically in Fig. 1. Second, named ^SSSDSA, we explore extending the nonautoregressive nature of the SaShiMi architecture for time series assignment with the appropriate conditioning. Third, we consider ^CSDIS4, which improves on the CSDI architecture and replaces the transformer layer operating in the time direction with the S4 model. In this way, the authors aim to evaluate potential improvements to the architecture that are more adapted to the domain of time series.

Related Research

Time series completion based on deep learning

A full discussion of time series completion is clearly beyond the scope of this work, even in the deep learning literature alone, so we refer the reader to recent reviews on this topic. Deep learning-based time series completion methods can be broadly categorized based on the techniques used.

(1) RNN-based approaches such asBRITS, GRU-D, NAOMI, and M-RNN use single or multi-directional RNNs to model time series. However, these algorithms suffer from diverse learning limitations, and many of them may only show suboptimal performance in diverse missing scenarios and different missing rates, as noted in recent studies.

(2) Generative models are the second major approach in this area. These include GAN-based approaches such as E2-GAN, and GRUI-GAN, and VAE-based approaches such as GP-VAE. Many of these have proven to be unstable in learning and unable to reach state-of-the-art performance. Diffusion models such as CSDI, the closest competitor to the authors' work, have also recently been considered with very strong results.

(3) Finally, there is a group of approaches that rely on modern architectures such as graph neural networks ( GRIN), permutation equivalent networks ( NRTSI), self-attention capturing time and feature correlation ( SAITS), control differential equation networks, and ordinal differential equation networks.

Conditional Generative Modeling with Diffusion Models

Diffusion models have been used for related tasks such as inpainting, especially in the image domain. With appropriate modifications, such methods from the image domain can be directly applied to the time series domain as well. Sound is a very specific time series, and diffusion models such as DiffWave, subject to different global labels and Mel spectrograms, have shown excellent performance in different sound generation tasks. Returning to the general time series, as already mentioned above, the closest competitor is CSDI; the main differences between the two approaches are (1) the use of SSMs instead of transformers, (2) a conceptually simpler setup of the diffusion process only in the time direction rather than in the feature and time direction, ( (3) the different learning objective of denoising only the segment being imputed (D1). In all experiments, we compare with CSDI.

time-series forecast

As noted above, time series forecasting can be viewed as a special case of time series completion in a suspended defect (BM) scenario. The literature on time series forecasting is even richer than the literature on time series completion. On the one hand, there are recursive general architectures such as LSTNet andLSTMa, and on the other hand, there are state-of-the-art architectures such as Informer, a very new transformer-based encoder-decoder design, which have shown excellent performance in long series prediction. Similarly, diverse methods such as GP-Copula, TransformerMAF, and TLAE have contributed significantly.

experiment

experimental procedure

In this paper, the (input) channel dimension is not retained as an explicit dimension during the diffusion process, but only implicitly by mapping the channel dimension to the diffusion dimension. This is inspired by the original DiffWave approach designed for single-channel audio data. As discussed below, this approach yields excellent results in scenarios where the number of input channels is limited to approximately 100 channels or less. This covers typical single-patient sensor data such as ECG or EEG in the healthcare domain, for example. When the number of input channels is large, the model often does not converge and has to resort to different learning strategies, for example by splitting the input channels. For this reason, the main experimental evaluation in this study focuses on datasets with less than 100 input channels.

Here we always train and evaluate the complementary model with the same missing scenarios and ratios. For example, it is trained with a 20% RM and evaluated based on the same settings. The reason for diversifying the dataset in this study is to show that the proposed method, in particular ^SSSDS4, is robust to a variety of qualitative data and a variety of baselines, and for this reason, experiments were conducted on healthcare-related datasets to show that the method is reliable in scenarios with high importance The performance metrics used in this study are The performance metrics utilized in this study are diverse. In all cases, a lower score means a better completion result. In most cases, we are comparing a single completion to a grand truth, while others incorporate a completion distribution and are therefore specific to stochastic completions.

time-series complement

On the proposed PTB-XL ECG dataset, SSSDS4 outperforms state-of-the-art complements

As a first dataset, we consider electrocardiogram (ECG) data from the PTB-XL dataset, which is interesting because ECG data must capture a consistent periodic structure of the signal over several beats to generate a coherent complement over random missing scenarios Represents a benchmark case: the ECG signal was preprocessed at a sampling rate of 100 Hz and L = 250-time steps (248 for ^SSSDSA ) was considered Three missing scenarios were considered, RM, NRM and BM, ^{includingCSDIS4,} SSSDSA ^andSSSDS4 We present the results for the diffusion model, considering its applicability for both study objectives D0 and D1. As baselines, we considered deterministic LAMC, and CSDI as strong stochastic baselines, and conditional adaptations of the original DiffWave architecture. We report the average of the MAE, RMSE, and CRPS for the 10 samples generated for each of the test subsets.

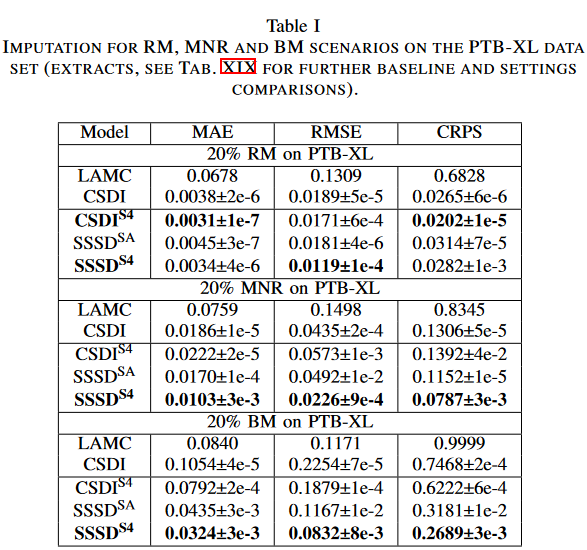
For all model types and defect scenarios, applying the diffusion process to a portion of the sample being imputed (D1) consistently produces better results than the diffusion process applied to the entire sample (D0). Therefore, in the following, we will limit our discussion to the D1 setting. We find that the proposed ^SSSDS4 significantly outperforms other completion models in most scenarios, especially in BM, where it reduces MAE by more than 50% compared to CSDI. in the BM scenario, ^SSSDS4 shows a small difference in the cumulative distribution function (CDF) of completion relative to the target CDF, with a CRPS of 0.2689, while the CSDI was 0.746. Similarly, it is noteworthy that the proposed ^SSSDS4 shows a clear improvement in time series attribution and generation in all settings, even though DiffWave shows very strong results as a baseline and is comparable to the more technically advanced ^SSSDSA in some scenarios. The S4 layer of ^CSDIS4 also shows clear improvements in CSDI in the RM and BM settings, especially in the RM scenario, where ^CSDIS4 outperforms the other methods with lower MAE and CRPS. The method assumes that the CSDI approach is useful in the RM setting, where feature and time consistency must be achieved. At the same time, ^{SSSDIS4 and} its variants show clear advantages in MNR and BM (and TF, discussed below), where time-dependent modeling is most important.

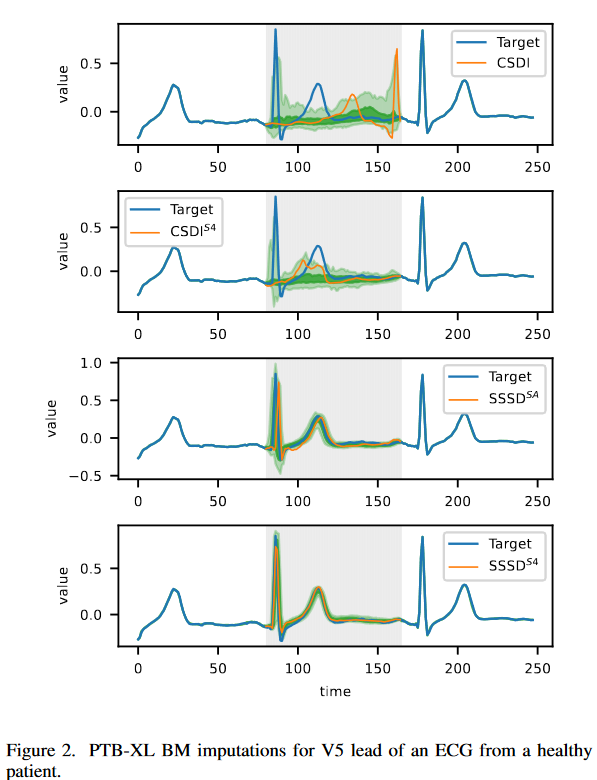
Existing approaches cannot generate meaningful BM completion

Fig. 2 shows the completion of the BM scenario for a subset of models in the PTB-XL completion task. The main objective is to demonstrate that the improvements achieved by the proposed approach lead to a better sample that is visible to the naked eye. The top left figure shows that state-of-the-art completion fails to produce meaningful completions. As an example, the identification of a QRS complex with a duration in the range of 0.08 to 0.12 seconds is considered a normal signal, but the model fails to detect the complex and rather displays a false R peak; ^CSDIS4 shows a qualitative improvement but lacks the essential signal; SSSDSA ^andSSSDS4 are the only two models that capture all essential signal features; ^SSSDS4 is superior to the task and can achieve qualitatively the best results, showing well-controlled quantile bands, as expected for a normal ECG sample.

^SSSDS4 has shown competitive completion performance compared to state-of-the-art approaches for other data sets and high loss rates.

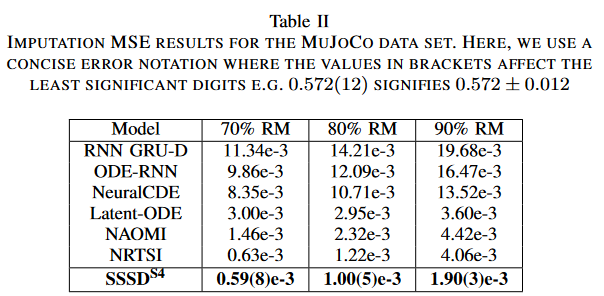
To show that SSSDS4 ^'s superior performance extends to additional datasets, we collected the MuJoCo dataset from NRTSI and tested ^SSSDS4 on very sparse RM scenarios such as 70%, 80%, and 90%, against baseline RNN GRU-D, ODE-RNN, NeuralCDE, Latent-ODE, NAOMI, and NRTSI and compared their performance. We report the average MSE of the single completion per sample on the test set over three trials. All baseline results were collected from NRTSI.

Table II shows the empirical RM results for the MuJoCo dataset, where ^SSSDS4 outperforms all baselines in all missing scenarios, especially at the highest RM ratio of 90%, where ^SSSDS4 achieves over 50% error reduction. The paper hypothesizes that a small percentage of condition values is sufficient for ^SSSDS4 to be able to properly reconstruct from time series signals of backward degenerative processes, as demonstrated in the experiments.

Performance of ^SSSDS4 on high-dimensional data sets

We also explored the potential of ^SSSDS4 for data sets with more than 100 channels, following the simple but suboptimal channel-splitting strategy described above.

The method implemented the RM completion task on the SAITSElectricity dataset, which contains 370 features with different missing rates of 10%, 30%, and 50%. M-RNN, GPVAE, BRITS, SAITS, and SAITS variants were used as baselines; we report the average MAE, RMSE, and MRE from one sample generated per test sample over three trials.

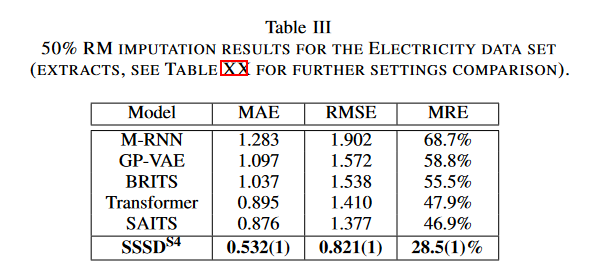
As shown in Table III, SAITS showed MAE, RMSE, and MRE of 0.876, 1.377, and 49.9%, respectively, while ^SSSDS4 showed 0.532, 0.821, and 28.5%, achieving a significant error reduction of 39.3, 40, and 39.2%, respectively. For the remaining RM settings, ^SSSDS4 also showed significant error reduction. Similarly, the 25% RM task forGRINwas tested on the PEMS-Bay and METR-LA datasets; on the PEMS-Bay dataset, ^SSSDS4 outperformed established baselines such as MICE,rGAIN, BRITS, andMPGRU on the MAE, MSE, and MREIn the METR-LA dataset, ^SSSDS4was again inferior to GRIN, but comparable to the remaining models.

time-series forecast

^SSSDS4 on the proposed data set

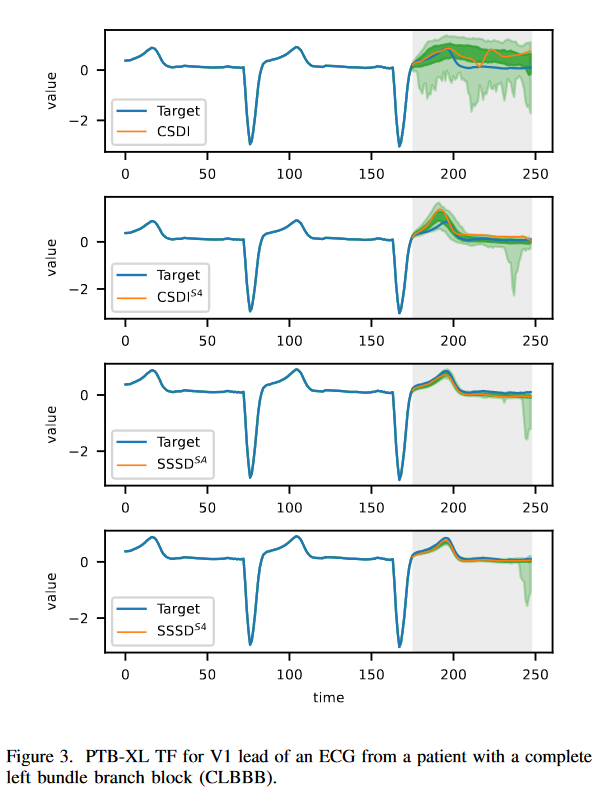
The CSDI, ^CSDIS4, ^SSSDSA, and ^{SSSDS4 models} were implemented on two datasets. For both, we report MAE, RMSE, and CRPS as indices for 10 samples generated for each test sample in three trials. First, this study again reconsidered the PTBXL from before, sampled at 100 Hz, but conditioned at 800-time steps, with L = 1000 time steps per sample for this task, and predicted at 200. ^SSSDSA outperformed MAE and CRPS by 0.087 and 0 ^SSSDS4 outperforms RMSE by 0.219, and ^CSDIS4 achieves smaller errors than CSDI on all three measures. The samples shown in Fig. 3 also show a clear improvement that can be seen by the naked eye.

^SSSDS4 offers competitive predictive performance compared to state-of-the-art approaches on a variety of data sets

In this study, the Solar dataset collected from GluonTS was tested with a forecasting task with condition values and forecast horizons of 168 and 24-hour steps, respectively. CSDI, GP-copula, Transformer MAF (TransMAF), and TLAE were considered as baselines. All baseline results were collected from their original papers; we report the average of the MSE and CRPS for the 10 samples generated per test sample over three trials.

For the solar dataset demonstration results, ^SSSDS4 achieved an error reduction of 60%, achieving 2.7e-2 for the MSE compared to 6.8e2 for the TLAE. Similarly, for the probabilistic measure CRPS, the strongest baseline, TLAE, reported 0.335, while ^SSSDS4 achieved 0.219, a significant error reduction of approximately 34%.

Finally, the cleverness of ^SSSDS4 was demonstrated on a traditional benchmark dataset for long-period forecasting. This study collected the preprocessed ETTm1 dataset from Informer and used it for forecasting in five different forecast settings. Prediction lengths were 24, 48, 96, 288, and 672-time steps, with condition values of 96, 48, 284, 288, and 384-time steps, respectively. The study was compared to LSTnet, LSTMa, Reformer, LogTrans, Informer, and one of its variants Informer(†) as a baseline. The paper reports the average of MAE and MSE for the test sample generated by the two trials.

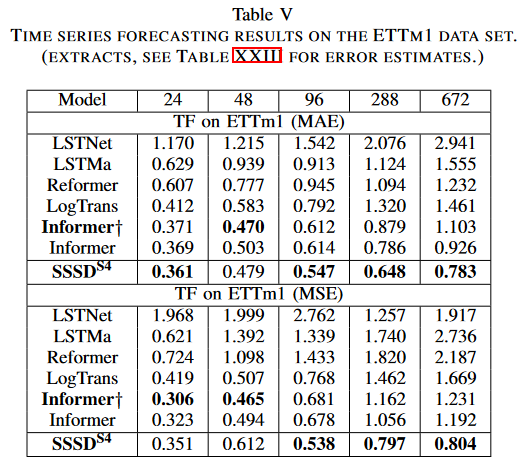
Experimental results again confirmed ^SSSDS4 's robust forecasting ability, especially for long-horizon forecasts with increasing conditional time steps. In the first setting, ^SSSDS4 outperformed the other baselines in MAE, but was close to Informer† 's score in MSE; in the second setting, ^SSSDS4 was comparable to Informer and Informer† in short forecast conditions and target length, but in the remaining three settings the ^SSSDS4 significantly reduced errors over the remaining baselines, obtaining, for example, 0.783 and 0.804 for MAE and MSE, respectively, compared to the strongest baseline Informer, which was 0.926 and 1.192, respectively.

summary

We propose a combination of a new model paradigm for sequential data with long-term dependence, the structured state-space model, and one of the current state-of-the-art approaches to generative modeling, the diffusion model. ^ssdss4 can be used in a variety of missing scenarios, we find that SSSDS4 improves the performance of existing state-of-the-art completions on a variety of data sets, with particularly high performance in pause missing and forecast scenarios. In particular, we have shown examples of qualitative improvements in completion quality that are visible to the naked eye. The proposed technique is very promising for generative models in the time series domain, opening up the possibility of building generative models conditional on various types of information, from global labels to local information such as semantic partition masks, thereby enabling a wide range of further downstream applications.

• 
• 
• 

Categories related to this article

• Article
• Time Series
• Time-series
• Diffusion Model