
Survey The Latest Transformers For Time Series
3 main points
✔️ Review Transformers for Time Series and focus on their strengths and limitations
✔️ Summary of Transformers in terms of network structure and applications
✔️ Suggestions for future development
Transformers in Time Series: A Survey
written by Qingsong Wen, Tian Zhou, Chaoli Zhang, Weiqi Chen, Ziqing Ma, Junchi Yan, Liang Sun
(Submitted on 15 Feb 2022 (v1), last revised 10 Feb 2023 (this version, v4))
Comments: Published on arxiv.
Subjects: Machine Learning (cs.LG); Artificial Intelligence (cs.AI); Signal Processing (eess.SP); Machine Learning (stat.ML)
code:

The images used in this article are from the paper, the introductory slides, or were created based on them.
summary
Transformers have demonstrated excellent performance in many tasks in natural language processing and computer vision, and have generated considerable interest in time series applications. Among the multiple advantages of transformers, the ability to capture long-range dependencies and interactions is particularly attractive for time series modeling and has led to remarkable advances in a variety of time series applications. In this paper, we systematically review transformer schemes for time series modeling and highlight their advantages and limitations.
In particular, it examines the development of time series transformers from two perspectives. From the network structure perspective, it summarizes the adaptations and modifications made to transformers to meet the challenges of time series analysis. From an application perspective, it classifies time-series transformers based on everyday tasks such as prediction, anomaly detection, and classification. As practical examples, robust analysis, model size analysis, and seasonal-trend decomposition analysis are performed to review how transformers perform in time series. Finally, future directions are discussed and suggested to provide useful research guidance.
Please refer to the references of the original papers for the sources of the papers reviewed in this paper.
Introduction
Transformerinnovations in deep learning[Vaswani et al., 2017] have attracted significant interest recently due to their superior performance in natural language processing (NLP) [Kenton and Toutanova, 2019], computer vision (CV) [Dosovitskiy et al., 2021], speech processing [Dong et al. ., 2018], and other areas [Chen et al., 2021b] have generated significant interest recently due to their superior performance. Over the past few years, a number oftransformervariants have been proposed to significantly advance state-of-the-art performance in various tasks: in NLP applications [Qiu et al., 2020; Han et al., 2021], in CV applications [Han et al, 2020; Khan et al., 2021; Selva et al., 2022], efficient Transformer [Tay et al., 2020], and attention models [Chaudhari et al., 2021; Galassi et al., 2020] from different aspects, quite Many literature reviews are available.
Transformers have shown excellent modeling capabilities for long-range dependencies and interactions in sequential data and have therefore been applied to time series modeling. To address the special challenges in time series modeling, many analogs of Transformer have been proposed, including prediction [Li et al. 2019; Zhou et al. 2021; Zhou et al. 2022], anomaly detection [Xu et al. 2022; Tuli et al, 2022], classification [Zerveas et al., 2021; Yang et al. For example, seasonality and periodicity are important features of time series [Wen et al., 2021a]. On the other hand, how to effectively model long- and short-range time dependence and capture seasonality simultaneously remains a challenge [Wu et al., 2021; Zhou et al., 2022]. Since Transformer for Time Series is an emerging challenge in deep learning, a systematic and comprehensive survey would greatly benefit the time series community. Several surveys exist related to deep learning for time series, including prediction [Lim and Zohren, 2021; Benidis et al. 2020; Torres et al. 2021], classification [Ismail Fawaz et al. 2019], anomaly detection [Choi et al, 2021; Bl ́ azquez-Garc ́a et al., 2021], and data augmentation [Wen et al., 2021b] were included, but Transformers for time series were barely mentioned.
This paper aims to fill that gap by summarizing the main developments in time series transformers. We propose a new taxonomy of time series transformers, both in terms of network modifications and application domains. For network modifications, we discuss the improvements made for both the low-level (i.e., modules) and high-level (i.e., architecture ) of transformers to optimize the performance of time-series modeling. For applications, transformers for common time series tasks including prediction, anomaly detection, and classification are analyzed and summarized. For each time series transformer, its insights, strengths, and limitations are analyzed. To provide practical guidelines on how to effectively use transformers for time series modeling, we conduct an extensive empirical study examining multiple aspects of time series modeling, including robustness analysis, model size analysis, and seasonal-trend decomposition analysis. Finally, we discuss possible future directions for time series transformers, including induced bias in time series transformers, time series transform ers andGNNs,pre-training of time series transformers, and time series transformers and NAS. This is the first comprehensive and systematic review of the major developments in transformers for modeling time series data.
Classification of Transformers in Chronological Order
To organize the existing time series transformers, we propose a taxonomy as shown in Fig. 1, in terms of network modifications and application areas. Based on this taxonomy, we systematically review the existing time series transformers. From the perspective of network modifications, we summarize the changes made at both the module and architectural levels of the transformers to address the particular challenges in time series modeling. From an application perspective, we classify time series transformers based on application tasks such as forecasting, anomaly detection, classification, and clustering.
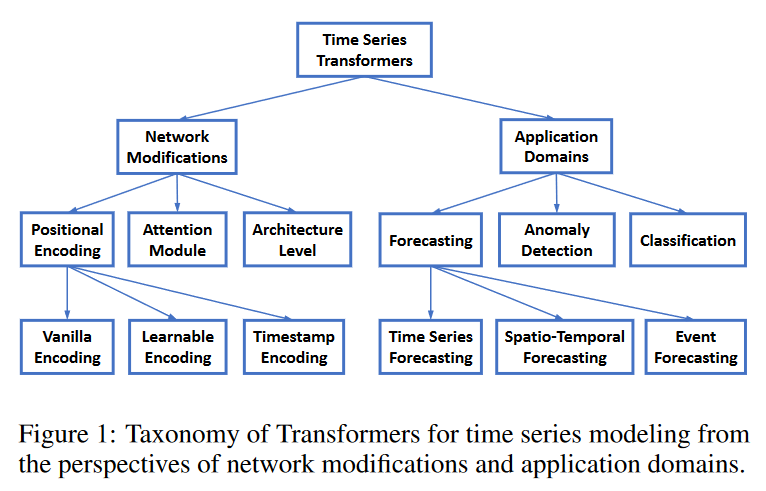
Network modification for time series
positional encoding
Since transformers are permutationally equivalent and the order of the time series is important, it is very important to encoding the positions of the input time series into the transformer. A typical design first encodes the location information as a vector, which is then injected into the model as an additional input along with the input time series. How these vectors are obtained when modeling the time series in the transformer can be divided into three main categories.
Vanilla positional encoding
Some studies [Li et al., 2019] simply introduced the vanilla position encoding used in [Vaswani et al., 2017] and added it to the embedding of the input time series to feed the transformer. While this plain application allows for some location information to be extracted from the time series, it fails to fully exploit important features of the time series data.
Learning-enabled position encoding
Several studies have shown that learning appropriate position encodings from time series data is more effective because vanilla position encodings are handmade and less expressive and adaptive. Compared to fixed vanilla position encodings, learned encodings are more flexible and can be adapted to specific tasks.
[Zerveas et al., 2021]introduced an embedding layer in the transformer, where the embedding vector for each position index is learned jointly with other model parameters. [Lim et al., 2019] used LSTM networks to encode position embeddings with the goal of better exploiting ordinal information in time series.
Timestamp encoding
When modeling time series in real-world scenarios, timestamp information is typically accessible in the form of calendar timestamps (e.g., seconds, minutes, hours, weeks, months, years) and unique timestamps (e.g., holidays, events). Although these timestamps are quite useful in real applications, they are rarely utilized in vanilla transformers. To alleviate this problem, Informer [Zhou et al, 2021] proposed encoding timestamps as additional location information by using learnable embedding. Similar timestamp encoding schemes have been used by Autoformer [Wu et al, 2021] and FEDformer [Zhou et al, 2022].
Attention Module
The heart of the transformer is the self-attachment module. It can be viewed as a fully connected layer with weights that are dynamically generated based on the pairwise similarity of input patterns. As a result, it shares the same maximum path length as the fully connected layer, but has far fewer parameters, making it suitable for modeling long-term dependencies.
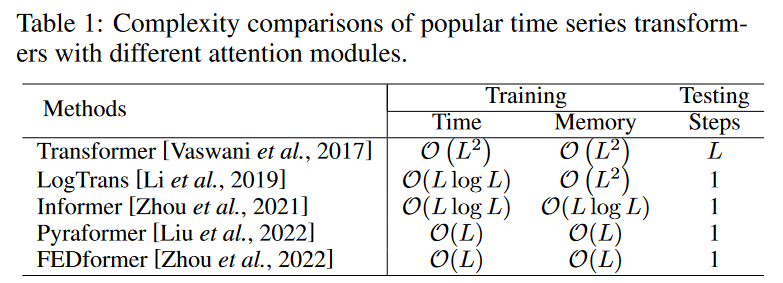
Vanilla transformer self-attention modules have a time/memory complexity of O(L2) (where L is the input time series length), which is a computational bottleneck when dealing with long time series. To reduce this secondary complexity, several efficient transformers have been proposed, which fall into two main categories.
(1)those that explicitly introduce sparsity bias in the attention mechanism, such as LogTrans [Li et al., 2019] and Pyraformer [Liu et al., 2022].
(2) Informer [Zhou et al., 2021] and FEDformer [Zhou et al., 2022], which explore low-rank properties of self-attention matrices to speed up computation; Table 1 provides a general summarizes both the time and memory complexity of the transformer.
Architecture-level innovation
In addition to adapting individual modules of the transformer to model time series, several studies [Zhou et al, 2021; Liu et al, 2022]have attempted to innovate the transformer at the architectural level. Recent work has introduced a hierarchical architecture to the transformer to account for the multi-resolution aspect of time series; Informer [Zhou et al, 2021]inserts a maximum pool layer of stride 2 between attention blocks and down-samples the series into its half-slice Sampling.
Pyraformer [Liu et al., 2022]designed aC-ary tree-based attention mechanism, with nodes at the finest scales corresponding to the original time series and nodes at coarser scales representing series at lower resolutions. Pyraformer has developed both within-scale and between-scale attention to better capture the time dependence across different resolutions. In addition to the ability to integrate information from different multi-resolutions, the hierarchical architecture also benefits from efficient computation, especially for long-time series.
Time Series Transformer Applications
The application of transformer stocritical time series tasks such as forecasting, anomaly detection, and classification will be reviewed.
Transformers in projections
Three types of forecasting tasks are discussed here: time series forecasting, spatial/temporal forecasting, and event forecasting.
Time Series Forecasting
Forecasting is the most common and important application of time series; LogTrans [Li et al., 2019]proposedconvolutionalself-attention by employing causal convolution to generate queries and keys in the self-attention layer. It introduces a sparse bias (Logsparse mask) in the self-attention model, which reduces the computational complexity from O(L) to O(Llog L).
Informer [Zhou et al., 2021] achieves similar computational improvements as LogTrans by selecting O(log L) dominant queries based on the query and key similarity instead of explicitly introducing a sparse bias.
It achieves the same computational improvements as LogTrans. It also designs a mold decoder that directly generates long-term forecasts, avoiding the cumulative error caused by one-step forecasting for long-term forecasts.
AST [Wu et al., 2020] uses a generative adversarial encoder-decoder framework. The encoder-decoder framework is used to learn as a parse-transformer model for time series prediction. It has been able to improve time series prediction by directly forming the adversarial network output distribution and by avoiding the accumulation of errors due to one-step-ahead inference. It also avoids the accumulation of errors due to one-step-ahead inference.
Autoformer [Wu et al., 2021] devised a simple seasonal trend decomposition architecture with an autocorrelation mechanism that works as an attention module. We devised a simple seasonal trend decomposition architecture in which the mechanism acts as an attention module. The autocorrelation block is not a traditional attention block. It measures the similarity of time delays between input signals and aggregates the top k similar subsequences to produce an output, reducing the complexity of O(Llog L).
FEDformer [Zhou et al., 2022] applies frequency-domain attention operations using Fourier and wavelet transforms. It achieves linear complexity by randomly selecting a fixed-size subset of frequencies; it is worth noting that the success of Autoformer and FEDformer has led to more attention in the community to explore self-attention mechanisms in the frequency domain for time series modeling The following is a list of some of the most important and promising new technologies that have been developed.
TFT [Lim et al., 2021] designs a multi-horizon prediction model with static covariate encoding. The multi-horizon prediction model with static covariate encoder, gating feature selection, temporalself-attentiondecoder, and temporalself-attentiondecoder is included. It encodes and selects useful information from various covariates for prediction. It also preserves globally incorporated interpretability. In addition, it preserves interpretability that incorporates time dependence, events, etc.
SSDNet [Lin et al., 2021] and ProTran [Tang and Matteson, 2021] combine Transformer and state-space models to provide probabilistic forecasts; SSDNet first uses Transformer to learn temporal patterns and estimate the parameters of the SSM, and then apply the SSM to perform seasonal trend decomposition to maintain interpretabilityProTran designs a generative modeling and inference procedure based on variational inference.
Pyraformer [Liu et al., 2022] designs hierarchical pyramidal attention modules with paths that follow a binary tree to capture different ranges of time dependence in linear time and memory complexity.
Aliformer [Qi et al., 2021] uses knowledge-guided attention and branching to modify and denoise attention maps to make sequential predictions for time series data.
Spatio-temporal Prediction
Spatio-temporal prediction requires consideration of both temporal and spatiotemporal dependencies for accurate prediction, and Traffic Transformer [Cai et al., 2020] has designed an encoder-decoder structure with an aself-attentionmodule to capture spatiotemporal dependencies and a Graph neural network module to capture spatiotemporal dependence and an encoder-decoder structure is designed. Spatialtemporal Transformer [Xu et al., 2020] for traffic flow prediction goes a step further. In addition to introducing a temporal transformer block to capture temporal dependencies, we also design an aspatial transformer block along with a graph convolution network to better capture spatial dependencies. The spatiotemporal graphtransformer [Yu et al., 2020]designs an attention-based graph convolution mechanism that can learn complex temporal-spatial attention patterns to improve pedestrian trajectory prediction.
Event Forecasting
In real-world applications, event sequence data with irregular and asynchronous timestamps are naturally observed. This is in contrast to normal time series data with equal sampling intervals. Event prediction is intended to
Event forecasting aims to predict the time and mark of future events from a history of past events, often modeled by a time point process (TPP) [Shchur et al., 2021].
Recently, several neural TPP models have begun to incorporate transformers to improve their event prediction performance.
The Self-attentive Hawkes process (SAHP) [Zhang et al., 2020] and the Transformer Hawkes process (THP) [Zuo et al., 2020] summarize the effects of historical events and calculate intensity functions for event predictionTransformer encoder architecture is employed to do this. They modify the position encoding by converting the time interval to a sinusoidal function so that intervals between events are available. Later, a more flexible attentive neural Datalog through time (A-NDTT) [Mei et al., 2022] was proposed to extend the SAHP/THP scheme to embed all possible events and times in the attention. Experiments show that it better captures sophisticated event dependencies than existing methods.
Transformers in anomaly detection
Deep learning also triggers novel developments for anomaly detection [Ruff et al., 2021]. Since deep learning is a type of representation learning, reconstruction models play an important role in the anomaly detection task. Reconstruction models aim to train a neural network that maps a vector from a simple predefined source distribution Q to the actual input distribution P + where Q is usually a Gaussian or uniform distribution, and P + is the number of possible anomalies in the input distribution. The anomaly score is defined by the reconstruction error. Intuitively, the greater the reconstruction error, i.e., the less likely it is from the input distribution, the higher the anomaly score. A threshold is set to distinguish between abnormal and normal.
Recently, [Meng et al., 2019]revealed the advantages of using transformers for anomaly detection compared to other traditional models for time dependency (e.g., LSTM ). In addition to higher detection quality (as measured by F1 ), transformer-based anomaly detection is significantly more efficient than LSTM-based methods, mostly due to the parallel computation of transformer architecturesTranAD [Tuli et al., 2022], MT- RVAEs [Wang et al., 2022], and TransAnomaly [Zhang et al., 2021], researchers in several studies, such as VAEs [Kingma and Welling, 2013] and GANs [ Goodfellow et al. 2014] and others have proposed coupling neural generative models with transformers.
TranADproposes an adversarial learning procedure to amplify the reconstruction error since simple transformer-based networks tend to miss small deviations in anomalies. an adversarial learning procedure in the form of a GAN is designed with two transformer encoders and two transformer decoders to obtain stability. The results of the isolation analysis show that the F1 score drops by nearly 11% when the transformer encoder-decoder is replaced, indicating that the transformer architecture is important for anomaly detection.
MT-RVAE and TransAnomaly are a combination ofVAEandtransformers, but they share different goals: TransAnomalycombinesVAE and transformers to enable more parallelization and reduce learning costs by nearly 80%, while TransAnomaly combines VAE and transformers to enable more parallelization and reduce learning costs by nearly 80%. In MT-RVAE, the multi-scale transformer is designed to extract and integrate time series information at different scales. It overcomes the shortcomings of conventional transformers, which extract only local information and analyze it sequentially.
Several time series transformers have been designed for multivariate time series that combine a transformer with a graph-based learning architecture such as GTA [Chen et al., 2021d]MT-RVAE is also for multivariate time series, but with fewer dimensions or insufficient close relationships between sequences.
This is the case where there are few dimensions or not enough close relationships between sequences such that the graph neural network model does not work well. Therefore, MT-RVAE modifies the position encoding module and introduces a feature learning module: the GTA has a graph convolutional structure and models the influence propagation process; like MT-RVAE, the GTA considers "global" information, but with vanilla multi-head attention. Instead, it employs a multi-branch attention mechanism, i.e., a combination of globally learned attention, vanilla multi-head attention, and neighborhood convolution.
That is a combination of global learned attention, vanilla multi-head attention, and neighborhood convolution.
AnomalyTrans [Xu et al., 2022] combines a transformer with Gaussian Prior-Association to make rare anomalies more distinguishable; it shares the same motivation as TranAD, but AnomalyTrans achieves this goal in a very different way to achieve this goal. In AnomalyTrans, prior and serial associations are modeled simultaneously. In addition to reconstruction loss, the anomaly model is optimized with a minimax strategy to constrain prior and serial associations to be more distinguishable.
Transformers in classification
Transformers have proven effective for a variety of time series classification tasks because they can capture long-term dependencies. Classification transformers typically employ a simple encoder structure where the self-attention layer performs representation learning and the feedforward layer generates probabilities for each class.
GTN [Liu et al., 2021] uses a transformer consisting of two towers, each of which acts on time-step-wiseandchannel-wiseattention, respectively. (also called "gating") is used to integrate the features of the two towers. The proposed transformer extension achieves the best results in the classification of 13 multivariate time series. [Rußwurm and Korner, 2020]studied a transform based on self-attention for the classification of raw optical satellite time series and compared it with recurrent and convolutional neural networks to achieve the best results.
Pre-trained transformers have also been studied in classification tasks. [Yuan and Lin, 2020] study transformers for time series classification of raw optical satellite images. The authors use a self-supervised pre-training schema due to limited labeled data. [Zerveas et al., 2021] introduce an unsupervised pre-training framework, where models are pre-trained on proportionally masked data. Pre-trained models are fine-tuned in downstream tasks such as classification.
[Yang et al., 2021] proposed using a large pre-trained speech processing model for the downstream time series classification problem, generating 19 dominant results on 30 common time series classification data sets.
Experimental Evaluation and Discussion
In this section, we conduct an empirical study to analyze how transformers perform on time series data. Specifically, we test different algorithms in different configurations on a typical benchmark dataset ETTm2 [Zhou et al., 2021].
Robustness Analysis
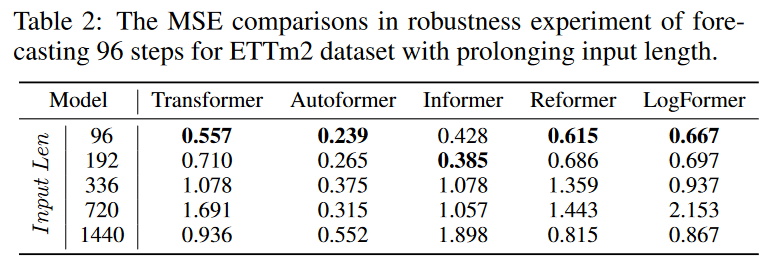
However, these studies have obtained the best results using short fixed-size inputs. It is questionable whether such efficient designs are used in practice. Therefore, we conducted experiments with longer input sequences to verify the predictive power and robustness of long input sequences.
As shown in Table 2, a comparison of the prediction results with longer input columns reveals that the varioustransformer-basedmodels degrade rapidly. This phenomenon means that many carefully designed transformers are not practical for long-term forecasting tasks because they cannot effectively utilize long-input information. More research is needed to fully exploit, rather than simply perform, long continuous inputs.
Model Size Analysis
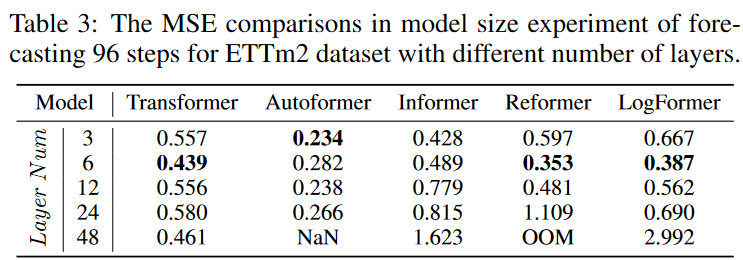
Before its introduction into the field of time series forecasting, Transformer showed dominant performance in the NLP and CV communities. [Vaswani et al, 2017; Kenton and Toutanova, 2019; Qiu et al, 2020; Han et al, 2021; Han et al, 2020; Khan et al, 2021; Selva et al, 2022]. One of the key advantages that transformers have in these areas is the ability to increase predictive power by increasing model size. Typically, model capacity is controlled by the number of layers in the transformer, which is typically set between 12 and 128 for CV and NLP.
However, as shown in the experiments in Table 3, when comparing prediction results for transformer models with varying numbers of layers, the shallowest transformers with 3 to 6 layers prevail. This raises the question of how to design an appropriate transformer architecture with deeper layers to increase model capacity and achieve better prediction performance.
Seasonal trend decomposition analysis
In their latest work, researchers [Wu et al., 2021; Zhou et al., 2022; Lin et al., 2021; Liu et al., 2022]have begun to realize the importance of seasonal-trend decomposition for transformer performance in time series forecasting. Table 4testsvariousattentionmodulesusing the moving-average trend decomposition architecture proposed by [Wu et al., 2021] as a simple experiment shown in the seasonal trend decomposition model can significantly improve the performance of the model from 50 % to 80 %. This is a unique block and such a performance boost due to decomposition seems to be a consistent phenomenon in time series forecasting for transformer applications and merits further investigation.

Future Research Opportunities
Here we highlight several potentially promising directions in the study of transformers in time series.
Induced bias toward time series transformers
Vanilla transformers make no assumptions about the patterns or properties of the data. It is a general and universal network for modeling long-range dependencies, but at the cost, i.e., that it requires a lot of data to train the transformer to avoid overfitting the data. One important feature of time series data is seasonality/periodicity and trend patterns [Wen et al., 2019; Cleveland et al., 1990]. Several recent studies have shown that incorporating series periodicity [Wu et al., 2021] and frequency processing [Zhou et al., 2022] in time series transformers can significantly improve performance. Thus, one future direction is to investigate ways to more effectively introduce induced bias into the transformer based on an understanding of time series data and specific task characteristics.
Transformers and GNN for time series
Multivariate and spatiotemporal time series are becoming increasingly common and require high-dimensional processing techniques, especially the ability to capture the underlying relationships between dimensions. The introduction of graph neural networks (GNNs) is a natural way to model spatial dependencies and relationships between dimensions. Recently, several studies have shown that the combination of GNNs and transformer/attention not only provides significant performance improvements, as in traffic forecasting [Cai et al., 2020; Xu et al., 2020] and multimodal forecasting [Li et al., 2021] but also provides a better understanding of spatiotemporal dynamics and a better understanding of potential coincidences have also been demonstrated. Combining transformers and GNNs to effectively perform spatial-temporal modeling of time series is an important future direction.
Pre-learning transformer for time series
Large-scale pre-trained transformer models have significantly improved the performance of various tasks in NLP [Kenton and Toutanova, 2019; Brown et al., 2020] and CV [Chen et al., 2021a]. However, research on pre-trained transformers for time series is limited, and existing work focuses mainly on time series classification [Zerveas et al., 2021; Yang et al.] Therefore, how to develop suitable pre-trained-transformer models for various tasks in time series remains a topic for future investigation.
Transformer with NAS for time series
Hyperparameters such as embedding dimension, number of heads, and number of layers have a significant impact on transformer performance. Manually setting these hyperparameters is time-consuming and often results in suboptimal performance. Neural architecture search (NAS) [Elsken et al., 2019; Wang et al., 2020] is a popular method for discovering effective deep neural architectures, and automation of transformer design using NAS in NLP and CV has been also seen in [So et al. 2019; Chen et al. 2021c]. Automatically discovering transformer architectures that are both memory and computationally efficient for industrial-scale time series data, which can be high-dimensional and long, is of practical importance and an important future direction for time series transformers.
summary
This paper provides a comprehensive survey of time series transformers in a variety of tasks. The reviewed methods are organized in a new taxonomy consisting of network modification and application domains. Representative methods in each category are summarized, their strengths and limitations are discussed through experimental evaluation, and directions for future research are highlighted.
Categories related to this article









