【Double Descent】なぜ「大きなモデル」と「大きなデータセット」が重要なのか

Neural Network 2024年07月25日

3つの要点

✔️ Double Descent（二重降下）とは、過学習のために増加した誤差が、さらなる学習により減少に転じる現象である。
✔️ モデルを大きくするとDouble Descent が生じるが、エポック数でも同様の現象が見られた。
✔️ Double Descent が生じるかどうかを論じるために、有効モデル複雑性 effective model complexity と呼ばれる新しい指標を作った。

Deep Double Descent: Where Bigger Models and More Data Hurt
written by Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever
(Submitted on 4 Dec 2019)
Comments: G.K. and Y.B. contributed equally
Subjects: Machine Learning (cs.LG); Computer Vision and Pattern Recognition (cs.CV); Neural and Evolutionary Computing (cs.NE); Machine Learning (stat.ML)

code：

本記事で使用している画像は論文中のもの、紹介スライドのもの、またはそれを参考に作成したものを使用しております。

はじめに

統計的学習理論には「バイアス・分散トレードオフ（bias-variance trade-off）」という概念があります。バイアスか分散かの二者択一という意味ですが、別の言い方をすると、モデルが単純すぎてもダメで複雑すぎてもダメということです。

モデルのパラメータが少なすぎると、データのパターンに対応できずに誤差が生じます。これを「バイアスが大きい」といいます。そして逆に、パラメータが多すぎると、訓練データにフィットしすぎてテストデータに対応できません。これを「分散（バリアンス）が大きい」といいます。つまり、あるデータ（タスク）には、最適なモデルの大きさがあるということを bias-variance trade-off は指摘しているわけです。

このことは古典的な統計的機械学習で言われてきたことですが、ニューラルネットワークでも成り立つと言われていました。ところが本論文では、近年のディープラーニングではこのトレードオフは常に成立するわけではない、と指摘しています。

トレードオフが正しいのであれば、あるタスクにおいてモデルサイズを増やし続けると、バリアンスが増加するため（過学習するため）にモデルの性能は下がるはずです。そして多くの場合、その通りです。しかし著者等はさらにモデルの大きさを増やしました。すると過学習のせいで増加した誤差が、また下がり始める現象が見られました。この現象こそがDouble Descent（二重降下）です。

このことから「モデルは大きければ大きいほどよい」ということが示され、今日の「論理ではなくパワーでぶん殴る」ような風潮が生まれ、世界的なGPUの争奪戦が始まったと言われています。

二重降下（Double Descent）の様子

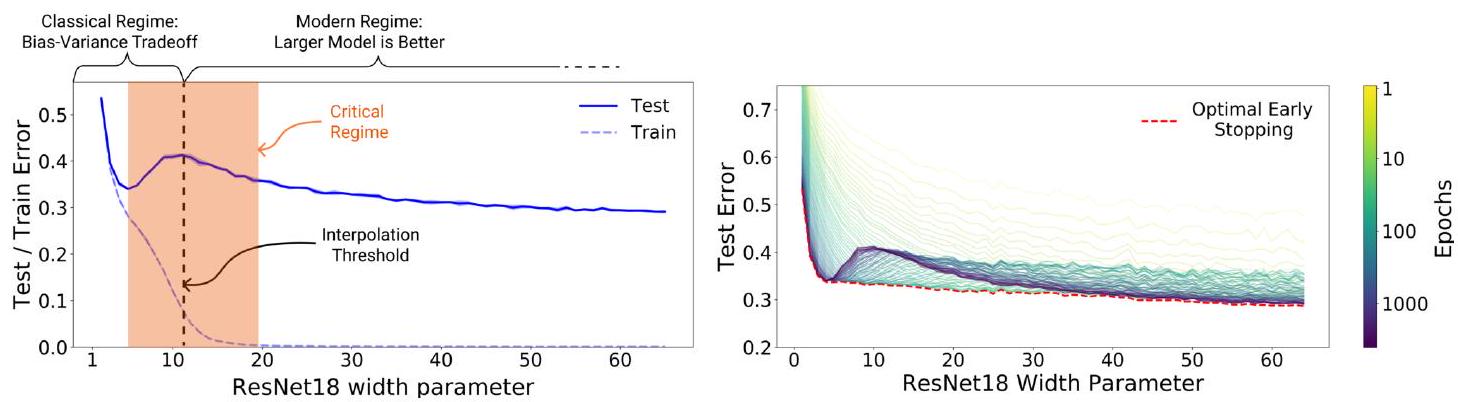
左図でDouble Descent を見てみましょう。

縦軸は誤差、横軸はパラメータ数です。バイアス・分散トレードオフによると、パラメータ数が多すぎても誤差は増えるのでしたね。左図の青い実線を見ると、確かにパラメータ数が5 あたりで誤差が増えています。しかしさらにパラメータ数を増やして、10あたりから誤差が減っていることもわかります。これがDouble Descent 現象です。ちなみに破線は、訓練データなので誤差は単調減少していますね（過学習）。

Double Descent 現象が生じることはわかったとして、どこまで誤差は降下するのか気になりますね。それを示したのが右図です。縦軸と横軸は左図と同じですが、エポック数で色分けしています。薄い色（黄色~黄緑）の部分を見ると、そもそもDouble Descent は生じていないように見えます。緑色（100 epochs）あたりでDouble Descent が生じており、青色（1000 epochs）あたりが最も降下量が大きいように見えます。つまり同じ大きさのモデルでも、エポック数が大きいほど誤差は小さくなる傾向にあることがわかります。

つまり「大きなモデルで何度も学習させると良い」というシンプルな結論が得られます。なお、ここで注意しておきたいのが、赤い破線（Early Stopping）です。右図からは「大きなモデルで何度も学習させると良い」という結論も得られますが、Eearly Stopping を利用するとより早く、誤差最小の状態を獲得することが可能であることもわかります。適切な時点で学習を止めれば、最良の結果が得られることを示しています。

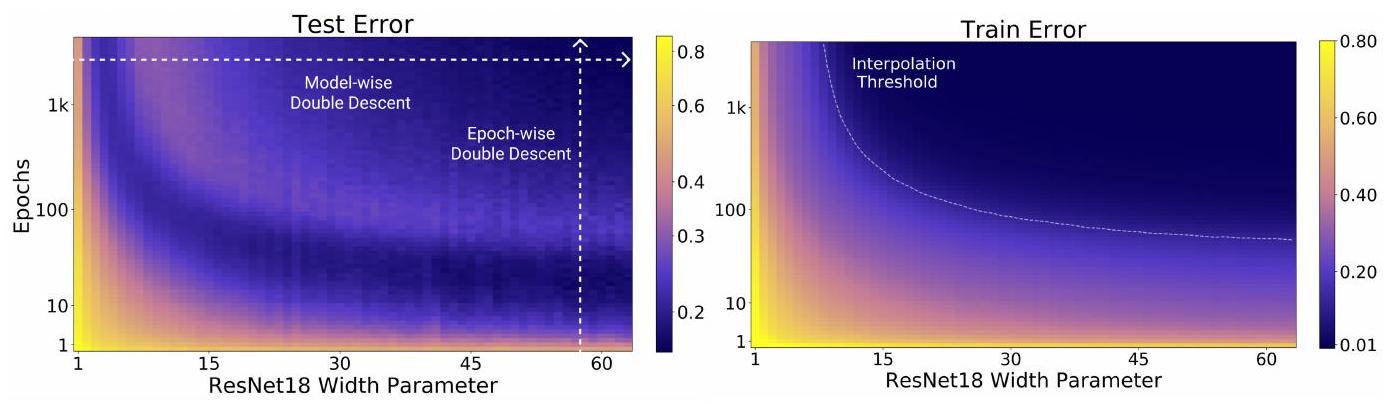
この図は、さきほどのDouble Descent の様子を別の方法で示したものです。横軸はパラメータ数で変わりませんが、縦軸がエポック数になりました。そして色が誤差を示しています。つまり左図のように縞模様に見える（同じ色が出てくる）のは、誤差が上下していることを示しており、Double Descent を別の方法で表現しています。

実験と結論

この論文では「モデルのパラメータを可変とする」、「エポック数を可変とする」、「訓練サンプルを可変とする」という3つの実験でDouble Descent が生じる条件が検討されました。

モデルはResNet18, 標準的なCNN, Transformer が利用され、データセットにはCIFAR-10, CIFAR-100, IWSLT'14, WMT'14 です。実験に使用したデータセットとモデルの組み合わせは以下のとおりです。

モデルの大きさによる二重降下 Model-wise Double Descent

Double Descent の導入で示したように、Model-wise Double Descent とは、モデルサイズを増やすと最初はテスト誤差が減少し、ある点を超えるとテスト誤差が増加し、さらにモデルサイズを増やすと再びモデル誤差が減少する現象です。

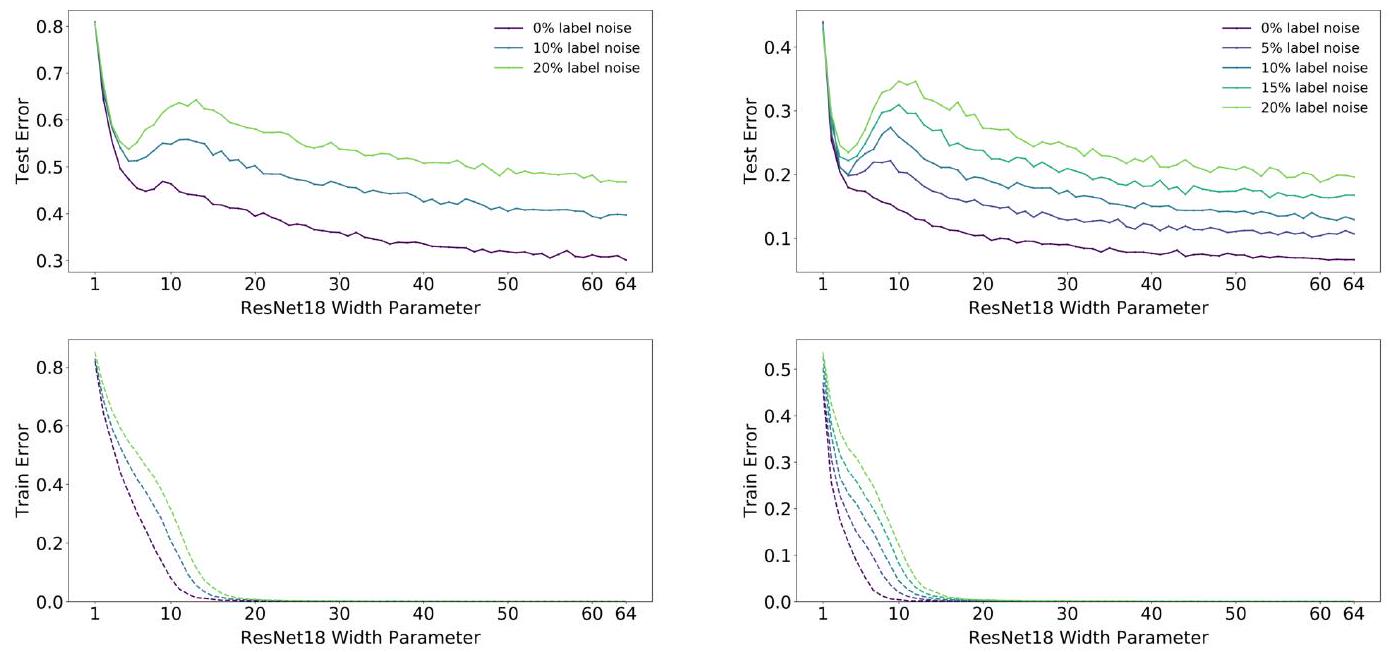
この図は、ResNet18とCIFARを使ってDouble Descent を評価したグラフです。ラベルノイズ（誤った正解を与えること）の程度によらず、あるモデルサイズでDouble Descent が観察されます。Double Descent が生じるモデルサイズを著者等は補間点（interpolation point）と呼んでいます。

ここでよく見ると、ラベルノイズが大きいほど補間点が右にシフトしていることがわかりますか? 論文の補足情報には、データ拡張の使用や訓練サンプルの増加も補間点を右にシフトさせることが示されています。つまりラベルノイズ、データ拡張、訓練サンプルの増加は、より大きなモデルサイズを要求するということです。

エポック数による二重降下 Epoch-wise Double Descent

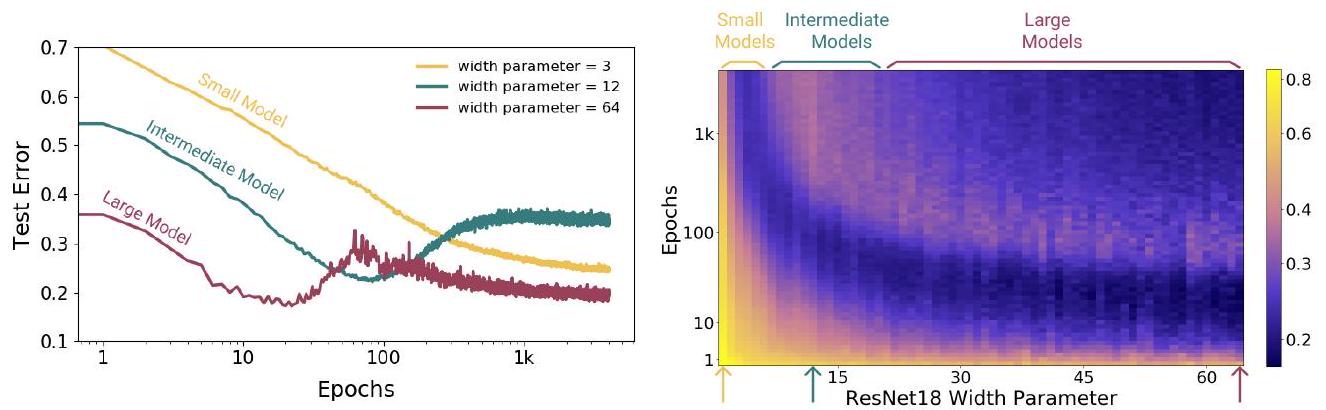この現象も導入部で説明しています。

この図で重要なことは、大きなモデルではDouble Descent が生じますが、小さい~中程度の大きさのモデルではDouble Descent は生じていないということです。さらに言えば、中程度の大きさのモデルではテスト誤差が増加した状態で学習が停滞してしまいます。

サンプル数による非単調性 Sample-wise non-monotonicity

サンプル非単調性 sample non-monotonicity とは、訓練データを増やすことが、必ずしもテストデータでの性能を向上させるわけではないという直感に反する現象です。

私たちはすでに Double Descent を見てきましたが、この現象は「パラメータを増やす」、「エポック数を増やす」ことについて言及されたものでした。サンプル非単調性は「訓練データ数」について、Double Descent が生じるかを議論します。

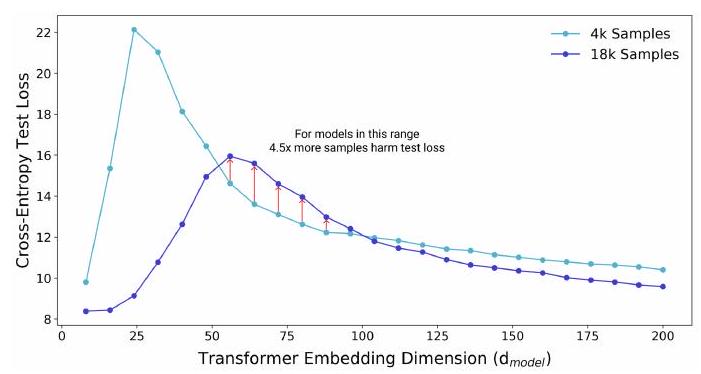
この図は、Transformer モデルのサイズ（埋め込み次元 $d_{\text {model }}$）と、言語翻訳タスク（IWSLT'14 German-to-English）におけるテストデータのクロスエントロピーロスの関係を示しています。

2つのモデル（4k, 18k）があります。直感では、18kの訓練データで学習したモデルは、常に4kで学習したモデルより性能が高いはずです。しかしながら、モデルサイズが50~100あたりでは、4kモデルの方がロスが小さいことがわかります。

このことは、訓練データセットの大きさによって、適切なモデルの大きさが決まることを示唆しています。このことからサンプル非単調性が指摘されています。逆に言えば、ある条件下では、訓練サンプルを増やしたせいで性能が下がることもあり得るということです。

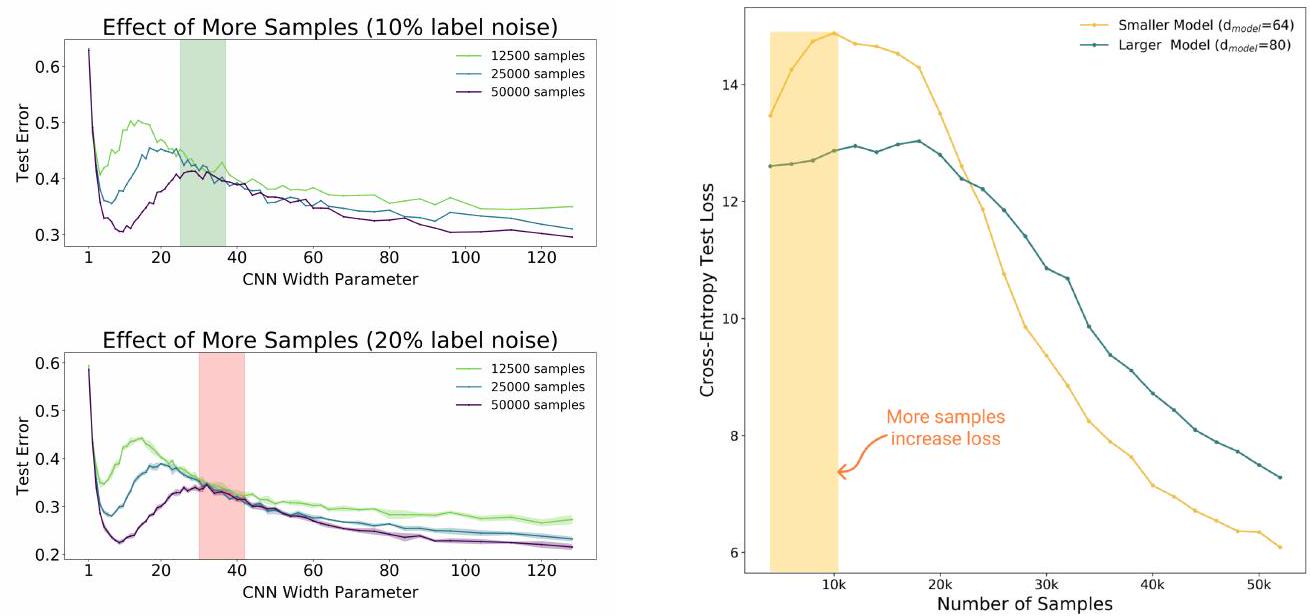
ここでは5層のCNNモデルとCIFAR-10で実験を行いました。左図で重要なことは、緑色の帯あるいは赤色の帯で示された領域において、各モデル（125k, 250k, 500k）のテスト誤差に大差はないということです。つまりモデルの大きさ、エポック数を固定したとき、訓練サンプル数を4倍に増やしてもモデルの性能は向上しないかもしれない、ということです。厳密に言えば、訓練サンプル数を増やしてもあまり意味がないようなモデルサイズがあるということです（左図の帯の部分ですね）。

右図は、Transformer とIWSLT'14 を使った実験です。ここでも同様の結果が生じています。むしろ黄色の帯の領域では訓練サンプル数の増加が、モデルの性能の悪化を引き起こしています。

モデルサイズや訓練データの量を単純に大きくすることが、必ずしもモデルの性能向上につながるわけではなく、特定の条件下では逆に性能悪化につながる可能性があることを示しています。このことからモデルの大きさと訓練データサイズのバランスが重要であることが示唆されます。

有効モデル複雑性 Effective Model Complexity

著者等は、有効モデル複雑性 Effective Model Complexity (EMC) と呼ばれる指標を提案し、Double Descent が生じる条件を定式化しました。

訓練手順 $\mathcal{T}$ とは、ラベル付き訓練サンプルセット $S=\left\{\left(x_{1}, y_{1}\right), \ldots,\left(x_{n}, y_{n}\right)\right\}$ を入力として受けとり、分類器 $\mathcal{T}(S)$ を出力するものと定義されます。このとき、手順 $\mathcal{T}$ （分布を $\mathcal{D}$ として）に対するECMは、訓練誤差がほぼ $0$ となる最大のサンプル数 $n$ として定義されます。

$$\operatorname{EMC}_{\mathcal{D}, \epsilon}(\mathcal{T}):=\max \left\{n \mid \mathbb{E}_{S \sim \mathcal{D}^{n}}\left[\operatorname{Error}_{S}(\mathcal{T}(S))\right] \leq \epsilon\right\}$$

$\operatorname{Error}_{S}(M)$ は、訓練サンプル数 $S$ を持つモデル $M$ の平均誤差を表しています。

仮説（一般Double Descent仮説）

自然なデータ分布 $\mathcal{D}$ 、ニューラルネットワークベースの学習手順 $\mathcal{T}$ 、十分に小さい $\epsilon>0$ に対して、分布 $\mathcal{D}$ から得た $n$ 個のサンプルで訓練した場合を考える。

パラメータ不足領域 under-parameterized regime

$\mathrm{EMC}_{\mathcal{D}, \epsilon}(\mathcal{T})$ が $n$ よりも十分に小さい場合、ECMを増加させる変更はテスト誤差を減少させる。

パラメータ過剰領域 over-parameterized regime

$\mathrm{EMC}_{\mathcal{D}, \epsilon}(\mathcal{T})$ が $n$ よりも十分に大きい場合、ECMを増加させる変更はテスト誤差を減少させる。

パラメータ適正領域 critically parameterized regime

$\mathrm{EMC}_{\mathcal{D}, \epsilon}(\mathcal{T})$ が $n$ に近い場合、ECMを増加させる変更は、テスト誤差を減少させるか増加させるかのいずれかになる。

この仮説は、モデルの複雑性を増加させることが一概に良いとは限らず、モデルの複雑性とトレーニングデータの量のバランスによって最適な性能が変わることを示唆しています。

まとめ

この論文では、あるモデルとその訓練手順において、訓練データ数がEMCに近しいときに非典型的な振る舞いが生じることを示しました。一般化Double Descent 仮説は、データセット、モデルアーキテクチャ、学習手順によらずに成り立つことが示唆されています。特に、model-wise double descent では、より大きなモデルに対して小さなデータセット（ECMを減少させる）を与えた場合には、性能が低下する可能性があることを示しました。また逆に、モデルの大きさ、データセット数、学習手順が適正であるとき、データセット数を増やす試みがかえって性能低下を引き起こすかもしれません。

この論文では「データセット数とモデルの大きさを適切に設定しましょう」という論調ですが、逆説的に、「より大きなモデル」と「より大きなデータ数」があれば精度があがるともいえます。本論文は「LLMのScaling Laws」と並んで重要な論文であると感じますね。