GANの発展の歴史を振り返る!GANの包括的なサーベイ論文の紹介(アルゴリズム編)
3つの要点
✔️様々な分野で使用されている 「GAN」の包括的なサーベイ論文の紹介
✔️アルゴリズム編では、「GAN」のアルゴリズムに焦点を絞って様々なアプローチを紹介
✔️ この記事で「GAN」の最新動向までをキャッチアップ可能
A Review on Generative Adversarial Networks: Algorithms, Theory, and Applications
written by Jie Gui, Zhenan Sun, Yonggang Wen, Dacheng Tao, Jieping Ye
(Submitted on 20 Jan 2020)
subjects : Computer Vision and Pattern Recognition (cs.CV); Machine Learning (cs.LG)
はじめに
2014年に画像生成のためのアルゴリズム「GAN」が発表されました。先日チューリング賞を受賞したYann LeCun氏は、GAN を「機械学習において、この10年でもっとも面白いアイディア」と評価しています。
GANの発表以降、GANに関する大量の論文が発表されており、2018にはGANに関係する論文が11800本発表されたとの報告があります。画像生成の枠組みで生まれたGANですが、今では自然言語処理や音声処理などの様々な分野で応用されています。
本記事では、GANの発展の歴史をアルゴリズムの側面から紹介します。
GANとは
GANとは、一言で表すなら生成器(以後、G)と識別器(以後、D)の二つが互いに敵対的な学習を行うというものです。
Gは生成した画像をなるべく本物に近づけるように、そしてDは入力された画像が本物か、それともGが生成した偽物か精度良く識別するように学習が行われます。これを表したものが以下の図です。
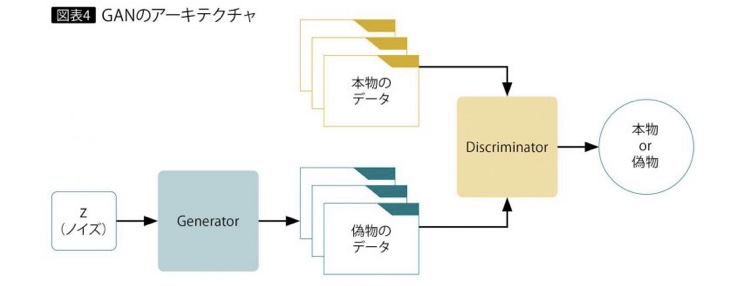
図1. GANの概要図
Gはノイズzから本物に近い画像を生成するように学習します。本物の画像とGが生成した画像の区別をDが出来なくなったとき、学習が収束します。つまり、Gは学習データの分布を学習できたということを表しています。
オリジナルのGANの損失関数は以下のように表せます。
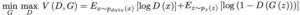
Gを固定して、Dの最適解を求めると以下のようになります。
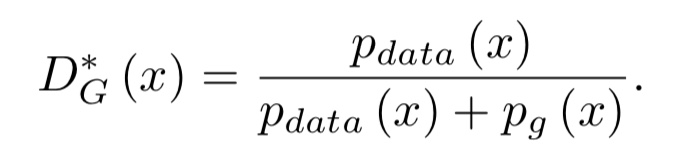
ここで、PgはGが獲得したデータの分布です。つまり、Pg=Pdataとなるとき、Dは1/2となります。
ここで、このD✳︎Gを元の式に代入すると、オリジナルのGANはJS距離と呼ばれるものを最小化する問題に帰着します。ここで、JS距離はKL距離を対称にした距離です。
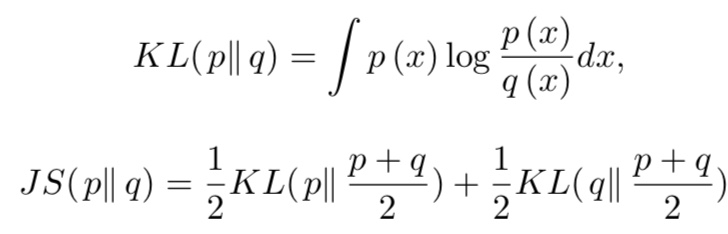
GANの問題点
GANは学習に大きな問題を抱えています。それは、勾配消失問題とモード崩壊です。下記の図はオリジナルのGANの損失関数をD(G(z))を軸に表したものです。
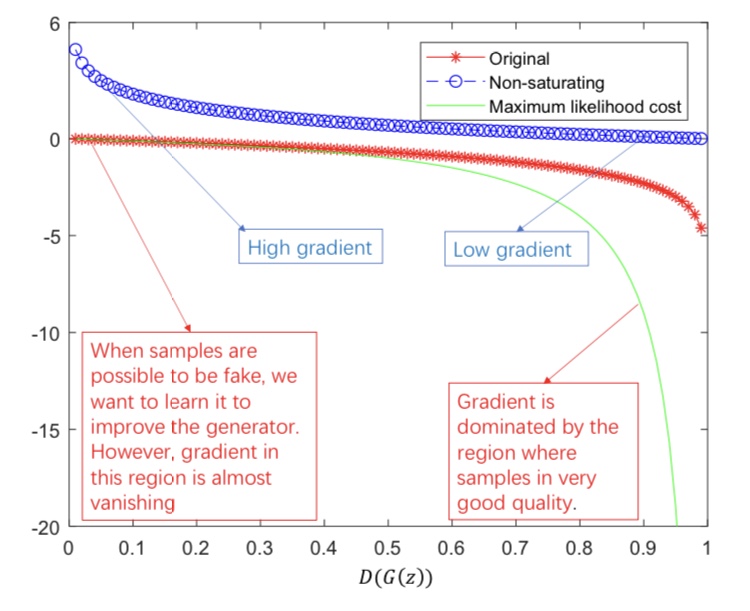
赤の線がオリジナルのGANを表しています。学習の初期には、本物のデータとGが生成するデータは簡単に判別できます。つまり、D(G(z))は0に近くなります。0付近ではほとんど勾配が0であり、Gの学習が十分に行われません。これを勾配消失問題と呼びます。
また、たまたまGがDを騙せる画像を生成した際に、その画像ばかり生成すれば損失関数は小さくなります。つまり、学習されたGは同じような画像ばかりを生成するようになります。これをモード崩壊と呼びます。
GANの代表的な亜種
では、ここからはGANの代表的な亜種を紹介していきます。
InfoGAN
オリジナルのGANでは、ノイズzをどう変更すれば画像が変わるか調整が難しいという問題がありました。InfoGANは、潜在変数cを用意し、相互情報量の最大化を行うことで、cに画像の特徴を埋め込むことに成功しました。下記の式が、InfoGANの損失関数です。
$V(D, G) − λI(c, G(c, z))$
上の式にあるように、 Gの生成する画像の情報をcに埋め込むように、学習が進みます。なぜ、相互情報量の最大化で、情報が埋め込めるのかは、こちらのサイトを参照してみて下さい。
Conditional GAN
Conditional GANはある条件の元、画像を生成するというものです。例えば、クラスラベルや文章特徴で条件付けて、それに対応する画像生成するというものがあります。
有名なConditional GANの例として、pix2pixが挙げられます。これは画像間のスタイル変換を行う手法です。以下の図は、白黒画像に色を付けるというタスクを表しています。
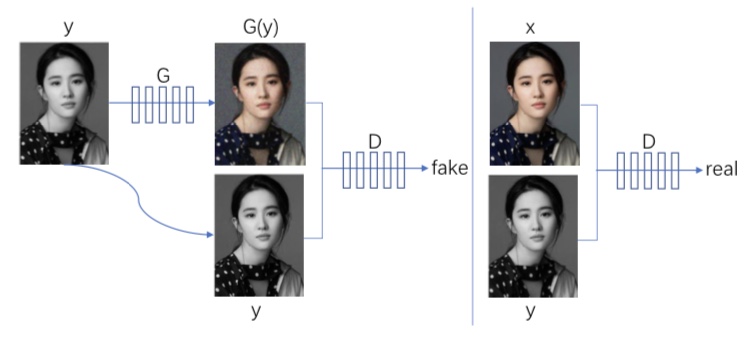
図2. 白黒画像に色を付けるpix2pixの例
pix2pixでは、元の画像yをGによって変換します。yと変換後の画像G(y)が本当のペアであるか、そして同時にxという本物の画像についても、xとyが本物のペアかであるか正確に識別するようにDの学習が進みます。
一方、 GはyとG(y)が本物のペアだとDに誤認識させるように学習を行います。これにより、Gは自然な変換の仕方を学習できます。(x,y)というペアで学習している点において、条件付きだと言うことが出来ます。
CycleGAN
CycleGANは、pix2pixに似ていますが条件設定が異なります。pix2pixでは画像ごとに1対1にペア(白黒画像と、それに対応した色の付いた画像など)が存在しています。しかし、ペアが得られないという場合も多々あります。例えば、馬とシマウマの画像はあるが、1対1に画像が対応してない場合などです。
このような場合でも、スタイル変換を行うことが出来るのがCycleGANです。下記の図はCycleGANの概要図です。
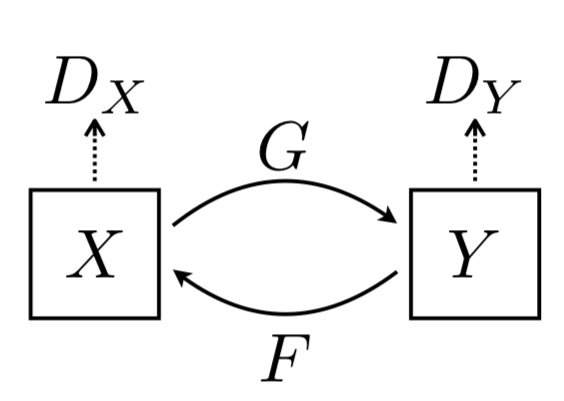
図3. CycleGANの概要
CycleGANには、二つの生成器G・Fと二つの識別器Dx・DYが存在します。Gを用いてxをyに変換し、それをDYによって識別します。yについても同様です。
このまま学習を行うと、ペアが存在していないため、スタイルだけでなく他の部分も変化してしまう可能性があります。そこで、CycleGANでは
$G(F(y)) = y, F(G(x)) = x$
となるように制約をかけることを提案しています。元に戻るという制約をかけることで、変換後の画像が復元可能、つまり大きく変化しないようにしています。
WGAN
WGANはGANの学習を安定させるために、Wasserstein距離と呼ばれる二つの分布間の距離測度を用いた損失関数を提案したGANです。
Wasserstein距離は、ある分布を対象となる分布に一致させるために必要な最小距離です。離散分布を用いるとイメージしやすいと思います。分布PとQがあり、PをQに一致させることを考えます。ここでは、以下のようなPとQを想定します。
P1=0.3, P2=0.2, P3=0.1, P4=0.4
Q1=0.1, Q2=0.2, Q3=0.4, Q4=0.3
この二つの分布を一致させるためには、P1からP2に0.2、P2からP3へ0.2、Q3からQ4へ0.1移動させることで、二つの分布を一致させることが出来ました。これを示したのが以下の図です。
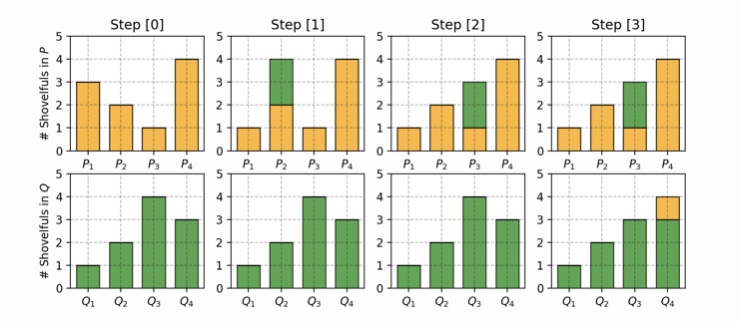
この合計がWasserstein距離(0.2+0.2+0.1=0.5)となります。これを連続分布に適応すると、以下のようになります。
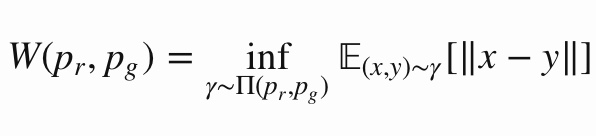
GANの問題点でも紹介しましたが、JS距離とW距離では何が異なるのでしょうか。この差分を見るために、以下のような想定でJS距離とW距離を計算してみましょう。
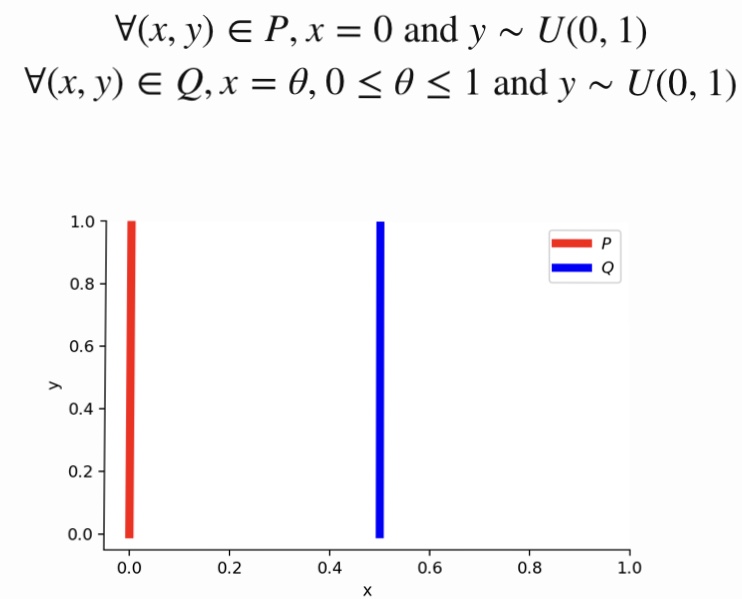
つまり、Pはx=0のみで確率値を、Qはx=θのみで確率値を持つ分布です。このとき、
JS距離=log2(θ≠0), W距離=$|θ|$
となります。θ=0のときはJS距離は0となり、不連続な関数であることが分かります。一方、W距離は連続であり、これがGANの安定した学習を可能にします。より詳細な議論はこちらのサイトをご覧下さい。
損失関数を工夫したGAN
GANの問題点の章でも述べたように、オリジナルのGANの学習は非常に不安定です。これを解決するために、様々な損失関数によるGANが提案されています。
LSGAN
LSGANは、非常にシンプルでありながらGの学習の初期における、勾配消失問題を解決する損失関数を提案しています。
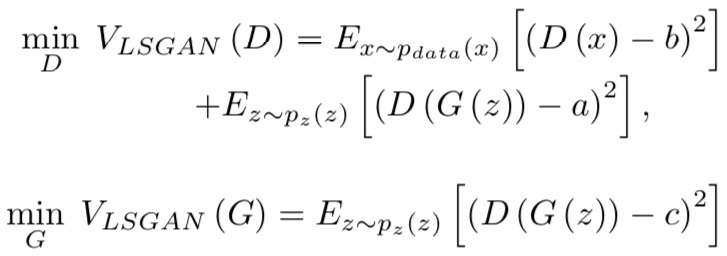
ここで、a,b,cはハイパーパラメータで、論文では、
a=0, b=1, c=1
などが推奨されています。二つ目の式からわかるように、学習の初期においてもc=1とすることで、Gの学習に十分な勾配が得られます。
Hinge loss based GAN
ヒンジロスを用いた損失関数を用いたGANも提案されています。
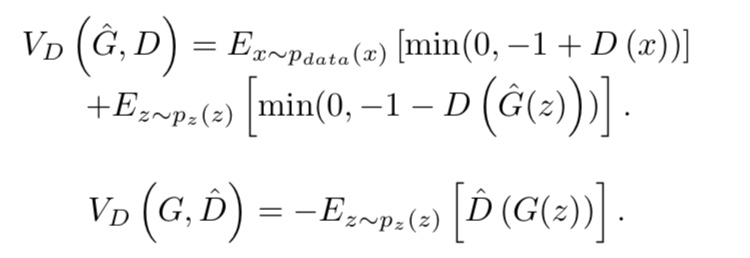
BEGAN
BEGANでは、Dはauto encorderとなっています。つまり、Dは本物の画像か、Gが生成した画像か明示的に識別しません。その代わりに、以下のWasserstein距離を最大化します。
W(μreal, μgen) = |mreal – mgen|
ここで、mrealは本物の画像の復元誤差で、mgenはGによって生成された画像の復元誤差です。Wを最大化するということは、本物の画像の復元誤差を0に近づけ、生成された偽物の画像の復元誤差を♾にするということです。
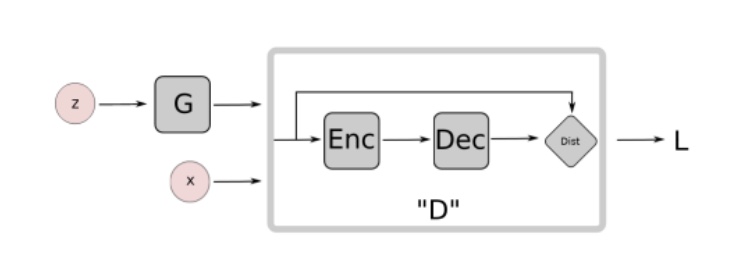
同時に、Gは自分自身が生成した画像の復元誤差を小さくするように学習します。つまりGはリアルな画像を生成することでしか、 GとDのどちらの学習を成功させることが出来ません。より詳細な議論はこちらのサイトをご覧ください。
GANの代表的な構造
DCGAN
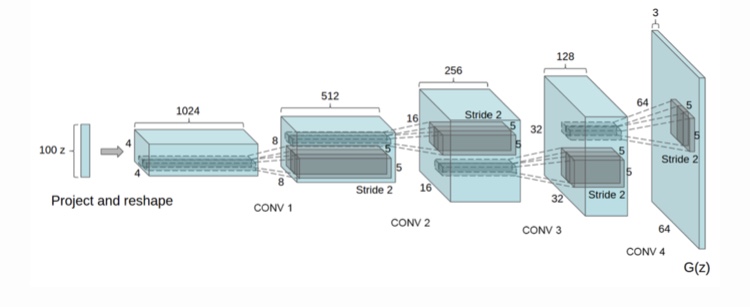
オリジナルのGANでは、GとDはMLP(多層パーセプトロン)で構成されていました。これに対して、DCGANでは、畳み込み層を用いて、GとDの表現力を高めています。下記の図はGに使用された構造の例です。
SAGAN
従来のGANの構造はCNNをベースにしており、局所的な部分に注目して画像生成してしまうという問題がありました。Self AttentionGAN(SAGAN)は、Self Attention機構をGANの構造に組み込むことで、大域的な特徴にも基づいて生成を行います。
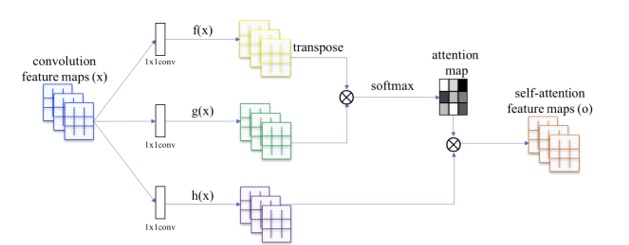
上図のf(x):クエリーとg(x):キーにより、各画素と似ている画素部分を抽出し、attention mapを生成します。その後、h(x):重みとattention mapを掛け合わせることで、Self Attetion mapを作成します。これを GANの構造に組み込むことで、より大域的な特徴を考慮した高品質の画像を生成することに成功しています。
StyleGAN
StyleGANは高品質の顔画像を生成することに成功したGANです。それだけでなく、StyleGANでは、髪・年齢・性別などをコントロールすることが可能です。下記の図がStyleGANの概要図です。
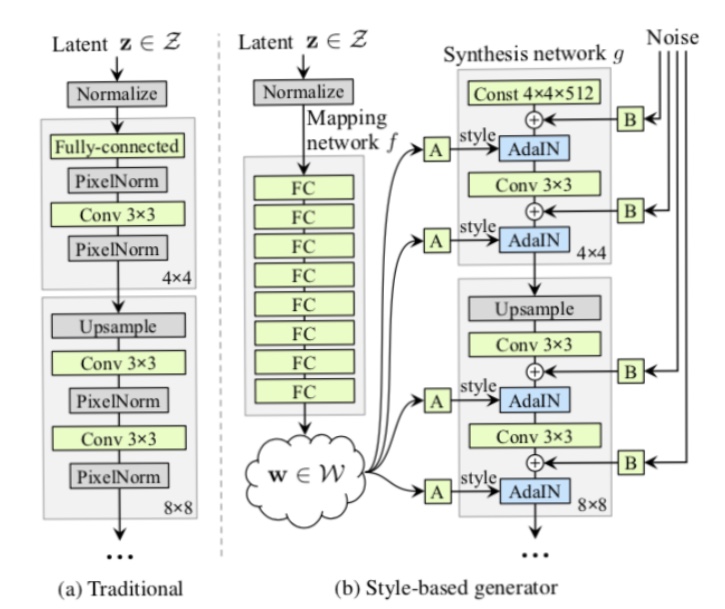
StyleGANでは、潜在変数zから直接画像を生成するのではなく、中間特徴量としてGのAdaIN部分に入力されます。ここで、AdaINは
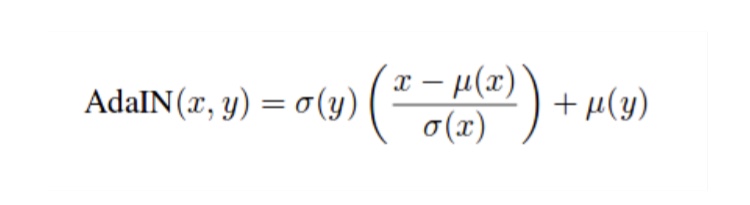
上記のように定義されます。xは入力で、yは画風変換を行いたいスタイル画像です。そのスタイル画像の平均$μ(y)$と標準偏差$σ(y)$を用いて変換することで、画風変換を行います。
学習によって、髪や性別などのスタイルが学習され、コントロール可能な変数となります。さらにStyleGANでは、ノイズをGの中間へ入力することで、髪の流れやそばかすなどを変化させることが可能です。
Progressive GAN
Progressive GANは低解像度の画像生成から初めて、徐々にレイヤーを追加していき高解像度の画像を生成することに成功したGANです。下記の図はProgressive GANの概要図を表しています。
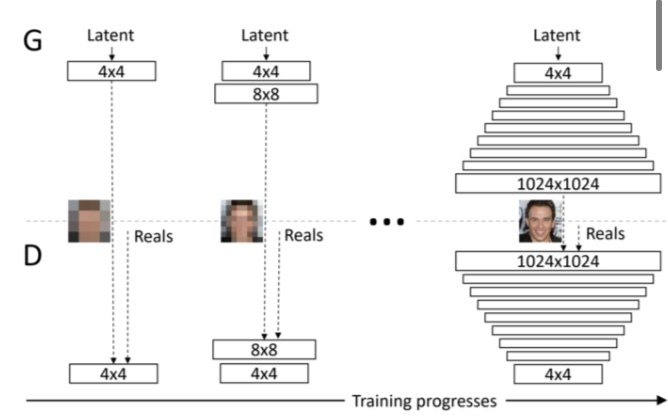
この構造の利点として、ノイズzからいきなり高画質の画像を再生するよりも、低画質の粗い画像の生成の方が簡単なタスクであるため、学習が簡単ということです。学習が簡単ということは、学習時間も削減できるという利点も発生します。
BiGAN
従来のGANでは、ノイズzから画像を生成するという一方向の学習のみを行っていました。BiGANでは、画像からzを生成するという双方向の生成の機構を導入することで、画像特徴量を得ることに成功しています。
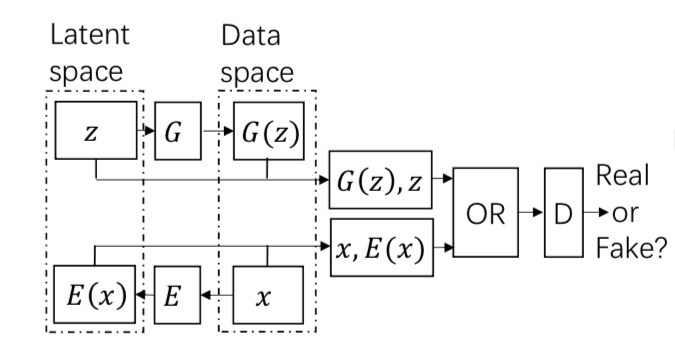
画像xはエンコーダEによって特徴抽出され、E(x)とzも含めて敵対的学習を行うことで、画像特徴量を抽出できるようにエンコーダを学習できます。
D2GAN
D2GANは、二つの識別器と一つの生成器から構成されるGANです。D2GANはモード崩壊を解決する手法となっています。
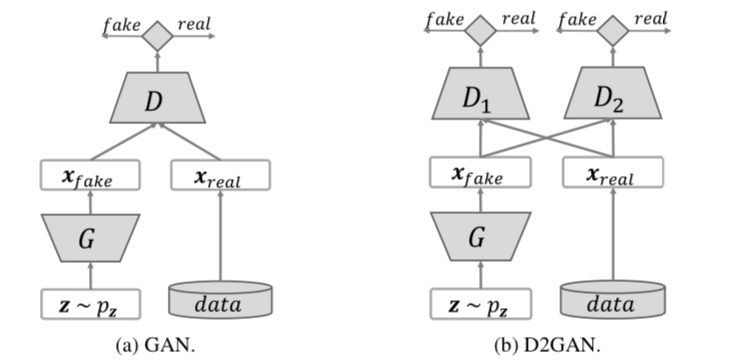
D2GANでは、損失関数がKL距離とreverse KL距離の重み付け和の関数となっています。つまり、損失関数は以下のようになります。
V(D, G) ∝ αKL(Pdata|Pg) + βKL(Pg|Pdata)
ここで、第一項がKL距離、第二項がreverse KL距離です。では、この二つの距離は何が異なるのでしょうか。
以下のような分布PとQを想定してみましょう。ここでは、QをPに近づけたいとします。
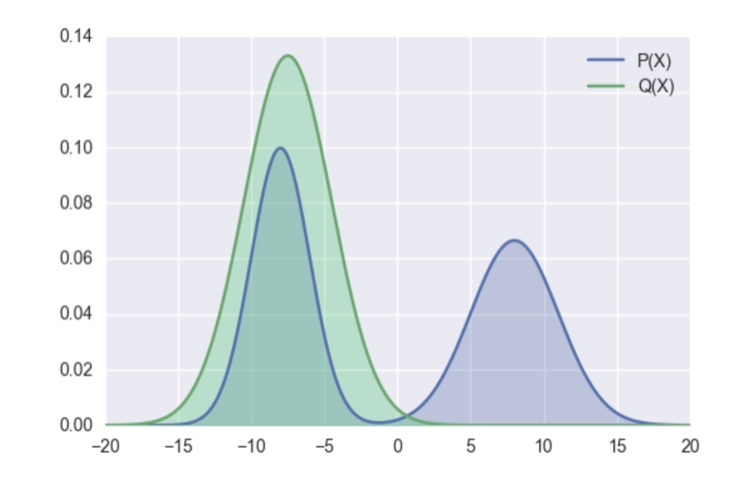
KL距離の場合、Pで重み付けされているため、KL距離は右の山によって大きくなってしまいます。KL距離を小さくしようとすると、右の山との距離を小さくしようとするため、以下のような分布となります。
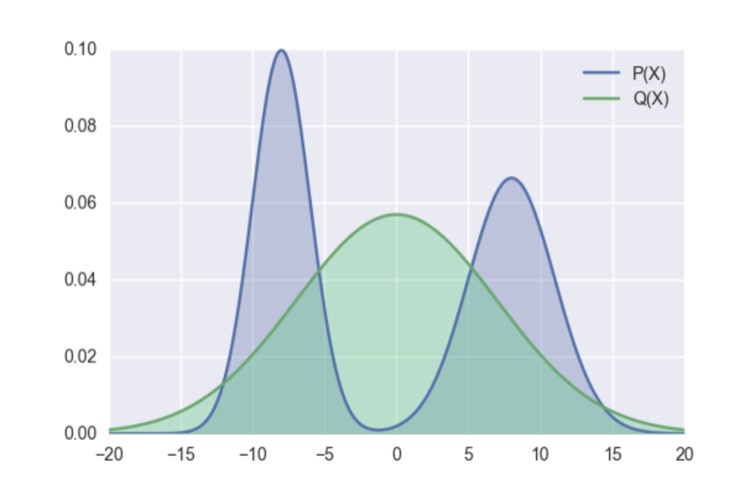
一方、reverse KL距離ではQで重み付けされているため、Pの右の山は無視されてしまいます。つまり、元の状態でKL距離が小さくなります。より詳細な議論はこちらのサイトをご覧下さい
つまり、D2GANの損失関数の最小化により、KL距離とreverse KL距離を小さくするということは、生成される画像の品質と多様性をパラメータで調整できるということです。αを大きくすれば多様性を、βを大きくすれば品質を重視するということです。
MGAN
MGANは、D2GANと対をなすもので複数の生成器と一つの識別器、そしてどの生成器から画像が生成されたか識別する分類器から構成されます。下記の図がMGANの概要図です。
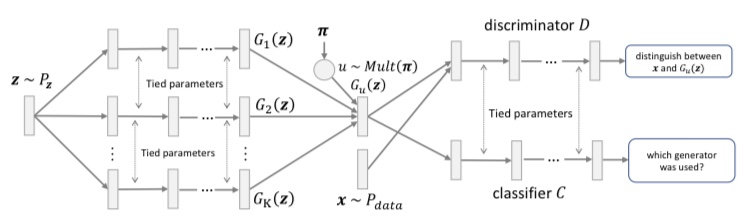
識別器は、複数の生成器が生成した画像を重み付けして得られる画像と本物の画像を識別するように学習されます。一方、それぞれの生成器の生成する画像分布のJS距離を最大化することで、各生成器が異なる画像を生成するようにします。
実際に画像を生成する際には、複数の生成器から一つ選択します。このように学習を行うことで、高品質な画像を生成でき、かつモード崩壊を防ぐことが出来ます。
まとめ
本記事ではGANの基礎から始め、これまでに提案されてきた様々なGANを紹介しました。オリジナルのGANは学習が不安定であるため、それを解決する手法がいくつも提案されています。
また、画像生成のタスクから始まったGANですが、現在では画像生成だけでなく、自然言語処理や音声処理など、様々なタスクに応用されています。次回はGANが生成する画像の品質を測る指標と、GANの応用について紹介します。
この記事に関するカテゴリー








