SSSD模型将扩散模型应用于时间序列数据的缺失完成问题。

三个要点
✔️ 应用扩散和结构化状态空间模型来补充缺失的时间序列数据，这是实践中的一个关键问题
✔️ 该模型大大改善了以前完成算法的不良表现，这取决于故障情况
✔️ 同样的机制也应用于时间序列预测问题

Diffusion-based Time Series Imputation and Forecasting with Structured State Space Models
written by Juan Miguel Lopez Alcaraz, Nils Strodthoff
(Submitted on 19 Aug 2022)
Comments: Published on arxiv.
Subjects: Machine Learning (cs.LG); Machine Learning (stat.ML)

code：  

本文所使用的图片要么来自论文、介绍性幻灯片，要么是参考这些图片制作的。

摘要

本文提出了一种完成时间序列数据缺失值的新方法：因在DALL-E2、稳定扩散和其他方面的应用而闻名的扩散模型，在这里被应用于时间序列数据而不是图像。在许多现实世界的数据分析任务中，经常需要完成缺失值。在本文中，我们提出了SSSD，一个基于两种新技术的完成模型：一个最先进的生成模型，（条件）扩散模型，以及一个内部模型结构化的状态空间模型，它特别适合于捕捉时间序列数据中的长期依赖关系。经证明，在各种具有挑战性的数据集上，包括未能提供有意义的结果的停顿情况，以及各种缺失情况下，输出的概率归因和预测性能可媲美或超过最先进水平。

介绍。

丢失输入数据的原因有很多，包括数据输入不畅、设备故障和文件丢失。处理缺失的输入数据是机器学习应用的一个主要挑战，因为大多数算法需要没有缺失值的数据才能学习。不幸的是，正如以前的研究所证明的那样，数据完成的质量会对下游的任务产生重大影响，不充分的完成甚至会使下游的分析产生偏差，从而使人们对所获得的结果的有效性产生怀疑。

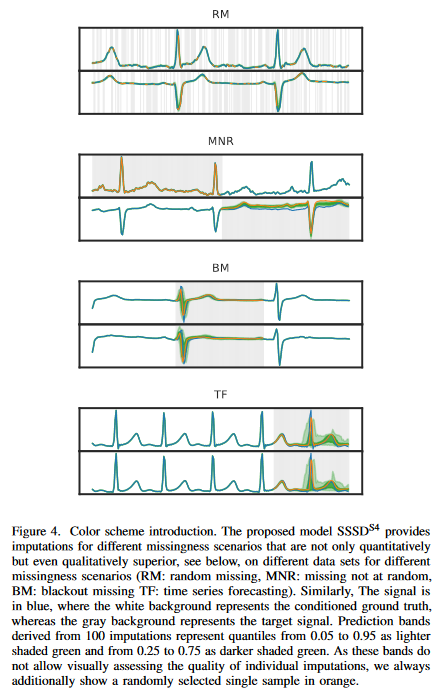
这项研究的重点是时间序列数据。然后考虑各种缺失情况（图4），即RM：随机缺失，MNR：非随机缺失，BM：暂停缺失和TF：时间序列预测。因此，时间序列预测可以被视为暂停缺失的情况之一，如果完成窗口的位置在序列的末端，就可以用统一的方式来讨论。还强调，处理作为非特定问题类别的完成度的最现实的方案是使用随机完成度方法。这并不是只提供一个单一的完成方式，而是允许对各种合理的完成方式进行抽样。因此，可以检查下游算法对完成度的敏感性，这代表了基于扰动的可解释人工智能方法的基础之一。最后，预测区间的广度提供了一种量化数据中固有不确定性的方法。

有大量关于时间序列完成的文献，从统计方法到自回归模型。最近，深度生成模型开始作为一种有前途的范式出现，用于模拟长序列的时间序列完成情况和长视野的时间序列预测问题。然而，许多现有的模型被限制在随机缺失的情况下，或在训练期间表现出不稳定的行为。在一些数据集中，即使是最先进的方法也未能在暂停缺失的情况下提供甚至是有质量意义的补充。

本研究旨在通过提出一种新颖的基于生成模型的时间序列补充方法来解决这些缺陷。本文使用扩散模型，更具体地说是在语音生成背景下提出的 DiffWave 框架，作为目前在不同数据模式下生成模型的最先进技术。第二个主要因素是使用结构化的状态空间模型，而不是使用扩展的卷积层和转换层作为模型的主要计算构件，这特别适合处理时间序列数据的长期依赖性。

综上所述，本文的主要贡献是

STRUCTURED STATE SPACE DIFFUSION（SSSD）模型，用于完成时间序列。

时间序列的补充

与时间序列数据一样，让_x0 是一个具有^RL×K 形状的数据样本。其中L是时间步数，K是特征或通道的数量。通常使用与输入数据的形状相匹配的二进制掩码，即imp_∈[0，1]^L×K ，其中条件值为1，0代表要补充的值。如果输入中存在缺失值，则需要一个相同形状的额外掩码_mmvi来区分输入数据中存在（1）和不存在（0）的数值。

文献中定义的不同缺失情景被分类但重述。随机缺失（RM）被定义为一种情况，即根据整个输入样本的所有通道的均匀分布，对归因掩码的零条目进行随机采样。接下来，非随机缺失（MNR）假设每个K的L个维度中的Xi缺失的随机子集为X0。最后，停电缺失（BM）假设在所有K的L维度的x0中存在一个缺失的xi子集。 如前所述，时间序列预测（TF）是BM完成的一个特例，其完成域跨越t个时间步骤的连续域。信号的颜色是蓝色的，白色背景代表条件地真值，灰色背景代表目标信号。完成后的预测带以浅绿色代表0.05至0.95的四分位数，以深绿色代表0.25至0.75的四分位数。由于这些带子不允许直观地评估单个完成的质量，在此总是随机选择的单个完成样本，另外显示为橙色。

扩散模型

扩散模型是一种生成模型，在各种数据模式中显示出最先进的性能，从图像到音频和视频数据。扩散模型通过依次学习去除噪声，从潜伏空间映射到信号空间，这些噪声在所谓的正向过程中连续加入马尔科夫，在逆向过程中被去除。因此，这两个过程是扩散模型的主干。前进过程的参数化如下。

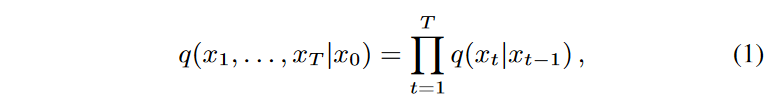
其中，q（xt|xt-1）=N（xt；√1-βtxt-1，βt1），（固定或可学习的）前向过程的方差βt是噪声水平的调整。等价地，xt可以用闭合形式表示为xt=√αtx0+（1-αt），对于∼N（0，1），其中αt=∑t i=1（1-βt）。

反向过程的参数化如下。

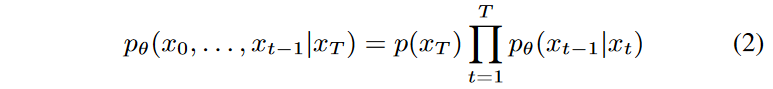
其中_xT ∼N（0，1）。同样，pθ(xt-1|xt)被假定为具有可学习参数的正态分布（具有对角线协方差矩阵）；Ho等人表明，在pθ(xt-1|xt)的特定参数化下，可以使用以下目标学习其逆。

其中D指的是数据分布，θ(xt, t)使用神经网络进行参数化。该目标可以被看作是负对数可能性的加权变异极限，当t较小时，即噪音水平较小时，该目标会降低条款的重要性。

对迄今为止描述的无条件扩散过程进行扩展，我们可以考虑一种条件性变形，即反过程是以额外信息为条件的，即θ=θ(xt, t, c)。这里，条件信息c的确切性质取决于当时的应用，范围从全局标签到频谱图。这里，它是由输入（根据完成掩码进行掩码）和完成掩码本身的串联给出的，即c = Concat(x0 (_{mimp mmvi}), (_mimpmmvi)(其中代表点状乘法)。在这项研究中，考虑了两种不同的设置（分别表示为D0和D1），其中扩散过程适用于整个信号或仅适用于互补区域。在任何情况下，方程（3）中的损失函数的评估被 假定为只对可获得地面真相的输入值 进行，即_mmvi =1。 对于D0，这是对应于（有条件获得的）完成屏蔽的非零部分的输入值的重建损失，以及完成屏蔽消失的输入标记在D1中，重建损失在结构上被消灭了。

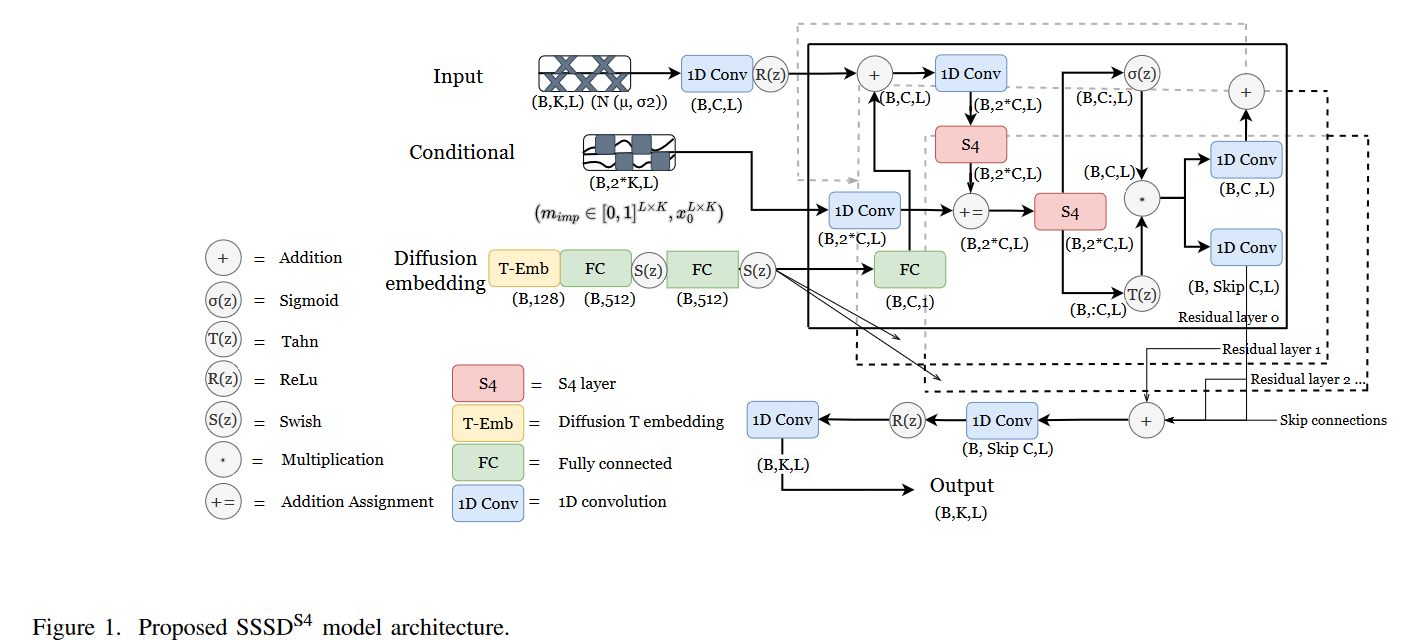
与Tashiro等人 一样，作者在 DiffWave架构 的基础上对θ(xt, t, c)进行了参数化；与Tashiro等人不同的是，我们在这里没有处理形状的扩展4D内部表示（批处理维度、扩散维度、输入通道维度和时间维度）。这是因为许多用于顺序数据的现代架构，如下面讨论的变换器和结构化状态空间模型，只能处理顺序的，即三维输入批次，因此需要交替处理时间和特征维度。在这里，我们采取了一种概念上更简单的方法，即把输入通道映射到扩散维度，只沿时间维度进行扩散。换句话说，我们处理的是批次（批次维度、扩散维度、时间维度）的几何图形。此外，我们通过使用S4层来修改DiffWave架构的内部结构，这比原始架构中使用的扩展卷积更适合处理时间序列数据。

状态空间模型

最近引入的结构化状态空间模型（SSM）代表了一种非常有前途的建模范式，特别是在捕捉时间序列中的长期依赖性方面。这个公式的核心是一个线性状态空间转换方程，它通过N维隐藏状态x(t)将一维输入序列u(t)连接到一维输出序列y(t)。这个过渡方程表示如下。

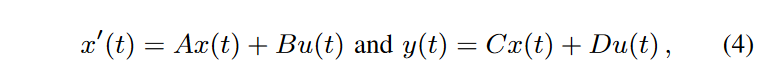
其中A、B、C和D是过渡矩阵。离散化之后，输入-输出关系可以写成卷积运算，在现代GPU上可以有效地评估。捕捉长期依赖关系的能力与根据HiPPO理论对A∈^RN×N的特定初始化有关。结构化状态空间模型（SSM）提出了结构化状态空间序列模型（S4），通过将上述SSM块的多个副本与适当的归一化层和变压器层风格的点序全连接层堆叠在一起，在各种序列分类任务上表现出卓越的性能S4.事实上，所得到的S4层可以被用来（加上适当的填充）替代变压器层、RNN层和一维卷积层，以参数化数据和形状之间的保形映射（批次、模型尺寸和长度尺寸）。 基于S4层，U通过S4层的组合，我们提出了一个用于序列生成的生成模型架构--SaShiMi，该架构受网络启发。虽然该模型是作为自回归模型提出的，但作者指出，已经可以使用（非因果）SaShiMi作为最先进的非自回归模型的组成部分，如DiffWave 。

建议的方法

作者提出了基于Diffwave的扩散模型的三种不同变体。首先，提出了^SSSDS4，一个有条件的DiffWave变体 ，并通过在添加扩散嵌入后将S4层替换为其每个剩余块内的扩散层，而不是双向扩展卷积来进行调整。作为第二项修改，在带有条件信息的加法赋值之后，还包括第二个S4层，在结合处理后的输入和条件信息之后，给模型提供了进一步的灵活性。这种结构在图1中得到了示意性的说明。第二，名为^SSSDSA，它探索了将SaShiMi架构的非自回归性质扩展到具有适当条件的时间序列分配。第三，作者考虑了^CSDIS4，它改进了CSDI架构，用S4模型取代了在时间方向运行的变压器层。通过这种方式，作者旨在评估对架构的潜在改进，使其更适应时间序列领域。

相关研究

基于深度学习的时间序列完成。

对时间序列完成的全面讨论显然超出了这项工作的范围，即使仅在深度学习文献中也是如此，因此应参考最近关于这一主题的评论。基于深度学习的时间序列完成方法可以根据所使用的技术进行大致分类。

(1) 基于RNN的方法，如BRITS、GRU-D、NAOMI和M-RNN使用单方向或多方向的RNN来模拟时间序列。然而，正如最近的研究所指出的那样，这些算法受到不同的学习限制，其中许多算法可能只在不同的缺失场景和不同的缺失率中显示出次优的性能。

(2) 生成模型是该领域的第二个主要方法。这些方法包括基于GAN的方法，如E2-GAN 、GRUI-GAN 和基于VAE 的方法，如GP-VAE 。其中许多已被发现在学习中不稳定，无法达到最先进的性能。扩散模型，如CSDI，是与作者的工作最接近的竞争者，最近也被考虑到了，结果非常好。

(3）最后，还有一组依靠现代架构的方法，如图神经网络（GRIN）、包络等效网络（NRTSI）、自我注意捕捉时间和特征关联（SAITS）、控制微分方程网络和序数微分方程网络。

扩散模型的条件生成式建模。

扩散模型已被用于相关的任务，如绘画，特别是在图像领域。经过适当的修改，这种来自图像领域的方法也可以直接应用于时间序列领域。声音是一个非常具体的时间序列，像DiffWave这样的扩散模型，受制于不同的全局标签和mel-spectrograms，在不同的声音生成任务中表现出优异的性能。回到一般的时间序列，如上所述，最接近的竞争者是CSDI；这两种方法的主要区别是：（1）使用SSM而不是变压器，（2）仅在时间方向而不是在特征和时间方向上对扩散过程进行概念上更简单的设置，((3)不同的学习目标，即只对被估算的部分进行去噪(D1)。在所有实验中，结果都与CSDI进行了比较。

时间序列预测

如上所述，时间序列预测可以被看作是悬浮缺陷（BM）情况下时间序列完成的一个特例。关于时间序列预测的文献甚至比关于时间序列完成的文献更丰富。一方面，有递归的通用架构，如LSTNet和LSTMa，另一方面，有最先进的架构，如非常新的基于变压器的Informer，其编码器-解码器的设计，在长序列预测中表现出优异的性能。同样，不同的方法，如GP-Copula 、TransformerMAF 和TLAE 也有很大的贡献。

实验

实验程序

在本文中，（输入）通道维度在扩散过程中并不作为一个明确的维度保留，而只是通过将通道维度映射到扩散维度来隐含。这是受最初为单通道音频数据设计的DiffWave方法的启发。正如下文所讨论的，在输入通道的数量被限制在大约100个通道或更少的情况下，这种方法会产生很好的效果。这涵盖了典型的单一病人传感器数据，例如医疗领域的ECG和EEG。当输入通道的数量增加时，模型往往不能收敛，不得不依靠不同的学习策略，例如通过分割输入通道。由于这个原因，本研究的主要实验评估集中在输入通道少于100个的数据集上。

在这里，补充模型总是用相同的缺失情况和比率进行训练和评估。例如，用20%的RM进行训练，并根据相同的设置进行评估。本研究中之所以将数据集多样化，是为了表明所提出的方法，特别是^SSSDS4，对多样化的定性数据和多样化的基线是稳健的，这就是为什么在与医疗有关的数据集上进行实验，以表明该方法在高度重要的场景中是可靠的本研究中使用的性能指标是方法的性能。本研究中所使用的性能指标是多种多样的。在所有情况下，较低的分数意味着更好的完成结果。在大多数情况下，对单一的完成度和地面实况进行比较，而其他情况则包含了完成度分布，因此是针对概率完成度的。

时间序列的补充

在拟议的PTB-XL心电图数据集上，SSSDS4的表现优于最先进的补充方案。

作为第一个数据集，我们考虑了来自PTB-XL数据集的心电图（ECG）数据，因为心电图数据需要在几个节拍上捕捉信号的一致周期性结构，以便在随机缺失的情况下产生一个连贯的补充，这很有趣代表一个基准案例：心电信号以100赫兹的采样率进行预处理，考虑L=250个时间步长（^SSSDSA为248个）；考虑三种缺失情况，RM、NRM和BM；^CSDIS4、SSSDSA^和SSSDS4。阐述了扩散模型的结果，以及它是否适用于D0和D1两个学习目标。作为基线，我们考虑了确定性的LAMC 、作为强随机基线的CSDI和原始DiffWave架构的条件适应。我们报告了为每个测试子集生成的10个样本的MAE、RMSE和CRPS的平均值。

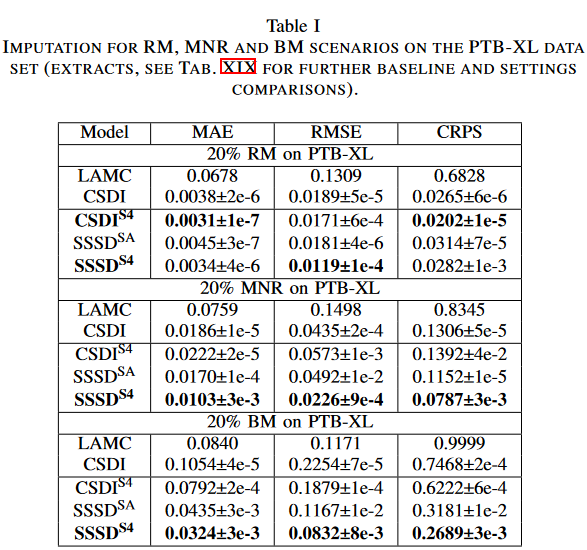
对于所有的模型类型和缺陷情况，将扩散过程应用于被估算样本的一部分（D1）始终比将扩散过程应用于整个样本（D0）的结果更好。 因此，下面的讨论仅限于D1环境。所提出的^SSSDS4在大多数情况下都明显优于其他互补模型，特别是在BM情况下，与CSDI相比，MAE降低了50%以上；在BM情况下，^SSSDS4显示出互补的累积分布函数（CDF）相对于目标CDF的差异较小，其CRPS为0.2689，而CSDI为0.746。同样，值得注意的是，尽管DiffWave作为基线显示出非常强大的结果，并且在某些情况下可以与技术上更先进的^SSSDSA相媲美，但拟议的^SSSDS4在所有设置中都显示出明显的改进。^CSDIS4的S4层也显示了在RM和BM设置中CSDI的明显改善，特别是在RM场景中，^CSDIS4以较低的MAE和CRPS超过了其他方法。该方法假定CSDI方法在必须实现特征和时间一致性的RM环境中是有用的，而^{SSSDIS4及其}变体在MNR和BM（以及TF，在下面讨论）中显示出明显的优势，在这些环境中，时间依赖性的建模最为重要。

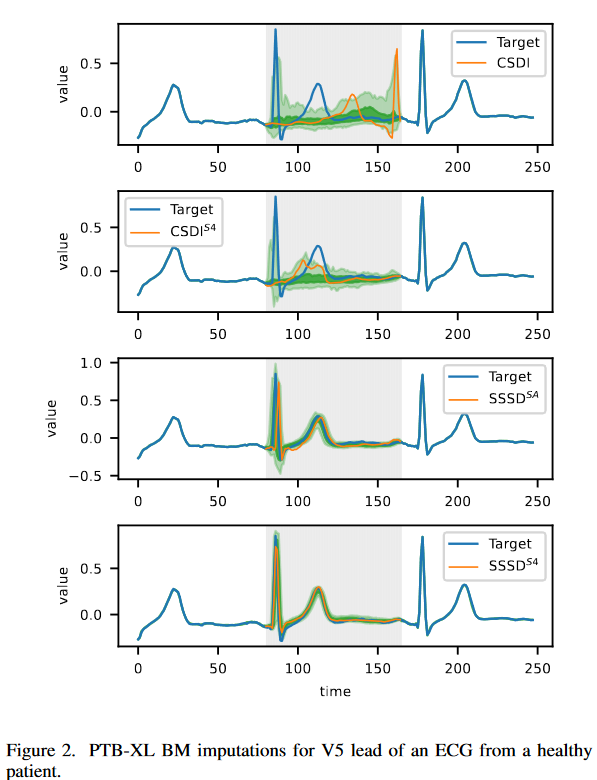
现有的方法不能产生有意义的BM互补性

图2显示了在PTB-XL补充任务中，BM场景与模型子集的补充情况。主要目的是证明所提出的方法实现的改进导致了肉眼可见的更好的样本。左上图显示，最先进的完成度未能产生有意义的完成度。作为一个例子，识别一个持续时间在0.08至0.12秒的QRS复合物被认为是一个正常的信号，但模型未能检测到该复合物，而是显示了一个错误的R峰；^CSDIS4显示了一个质量上的改善，但缺乏基本的信号；SSSDSA ^和SSSDS4是仅有的两个能捕捉到所有基本信号特征的模型；^SSSDS4在任务上更胜一筹，可以取得定性的最佳结果，显示出良好的控制量化带，这也是正常心电图样本的预期。

与最先进的方法相比，^SSSDS4在其他数据集和高损失率的情况下表现出有竞争力的互补性能。

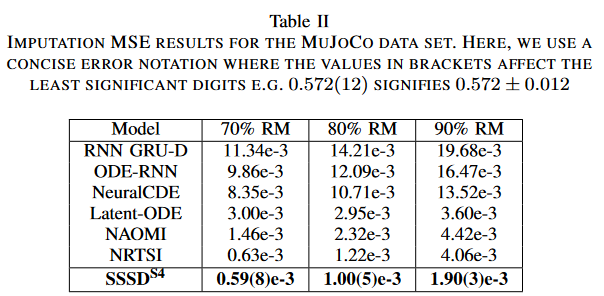
为了证明SSSDS4^的优越性能延伸到更多的数据集，我们从NRTSI收集了MuJoCo数据集，并在非常稀疏的RM场景下，如70%、80%和90%，对^SSSDS4与基线RNN GRU-D、 ODE-RNN进行了测试。 神经CDE、 Latent-ODE、 NAOMI和 NRTSI ，并比较其性能。我们报告了在三次试验中每个样本的单次完成的平均MSE。所有基线结果都是从NRTSI收集的。

表二显示了MuJoCo数据集的经验性RM结果，^SSSDS4在所有缺失情况下都优于所有基线，特别是在最高的RM比率为90%时，^SSSDS4实现了超过50%的误差降低。本文假设，小比例的条件值就足以让^SSSDS4能够正确地从时间序列信号中重建落后的退化过程，这在实验中得到了明确的证明。

^SSSDS4在高维数据集上的表现。

按照上述简单但次优的通道分割策略，^SSSDS4的潜力也被探索到了具有100多个通道的数据集。

该方法在SAITS电力数据集上实现了RM的完成任务，该数据集包含370个特征，缺失率分别为10%、30%和50%。M-RNN、 GPVAE、 BRITS、SAITS和SAITS变体被用作基线；我们报告了三次试验中每个测试样本产生的平均MAE、RMSE和MRE。

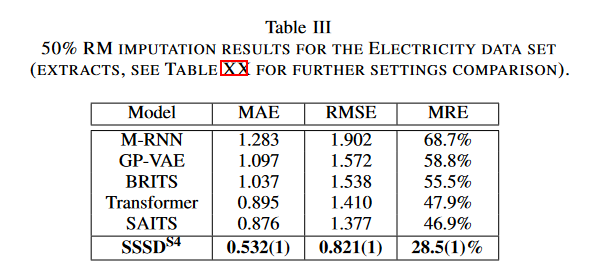
如表三所示，SAITS的MAE、RMSE和MRE分别为0.876、1.377和49.9%，而^SSSDS4则为0.532、0.821和28.5%，分别实现了39.3、40和39.2%的大幅降错。对于其余的RM设置，^SSSDS4也显示出明显的错误减少。同样，在PEMS-Bay和METR-LA数据集上测试了GRIN25% RM任务：在PEMS-Bay数据集上，^SSSDS4在MAE、MSE和MRE方面的表现超过了MICE、rGAIN、BRITS和MPGRU等既定基准。在METR-LA数据集中，^SSSDS4再次逊色于GRIN，但与其余模型相当。

时间序列预测

在拟议的数据集上的^SSSDS4。

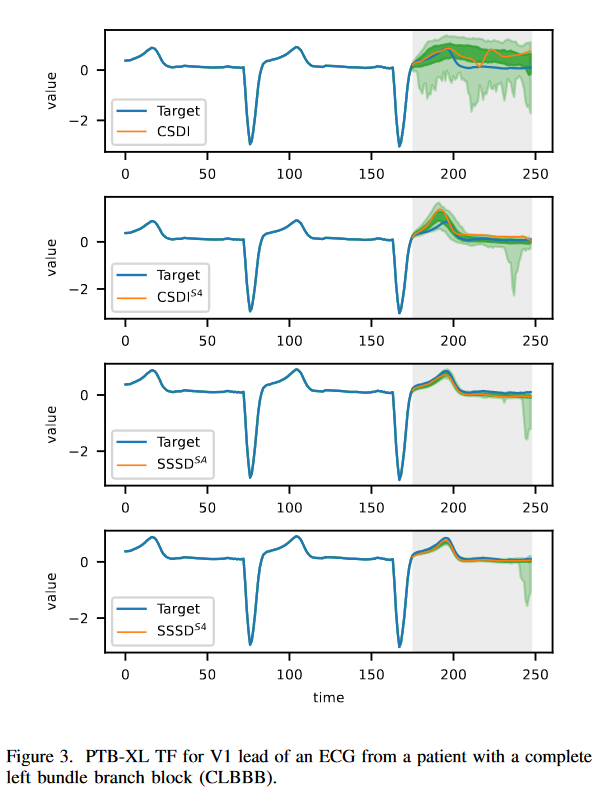
CSDI、^CSDIS4、^SSSDSA和^SSSDS4模型是在两个数据集上实现的。对于这两种情况，我们将MAE、RMSE和CRPS作为指数报告，每个测试样本在三次试验中产生10个样本。首先，本研究再次重新考虑了之前的PTBXL，以100赫兹采样，但以800个时间步数为条件，该任务每个采样的时间步数为L=1000，预测为200。^SSSDS4比RMSE高出0.219，^CSDIS4在所有三个指标上都取得了比CSDI小的误差。图3所示的样品也显示出明显的改进，肉眼可见。

与最先进的方法相比，^SSSDS4在各种数据集上提供了有竞争力的预测性能。

在这项研究中，从GluonTS收集的太阳能数据集在预测任务中进行了测试，条件值和预测范围分别为168和24小时步长。CSDI、GP-copula、Transformer MAF（TransMAF）和TLAE 被认为是基线。所有的基线结果都是从他们的原始论文中收集的；我们报告了三次试验中每个测试样本产生的10个样本的平均MSE和CRPS。

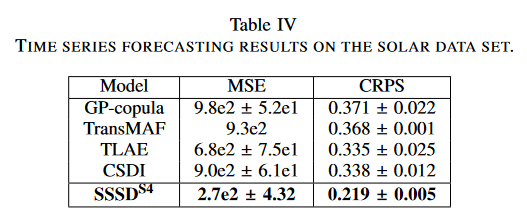
太阳能数据集的经验结果表明，^SSSDS4的MSE达到2.7e-2，而TLAE的MSE为6.8e2，误差减少了60%。同样，对于概率指标CRPS，最强的基线TLAE报告为0.335，而^SSSDS4达到了0.219，误差明显减少约34%。

最后，在一个传统的长周期预测的基准数据集上展示了^SSSDS4的聪明之处。该研究从Informer收集了预处理的ETTm1数据集，并在五个不同的预测设置中使用它进行预测。预测长度为24、48、96、288和672个时间步骤，条件值分别为96、48、284、288和384个时间步骤。该研究与LSTnet、 LSTMa、 Reformer、 LogTrans、Informer及其变体之一Informer(†)作为基线进行了比较。该文件报告了两次试验产生的测试样本的MAE和MSE的平均值。

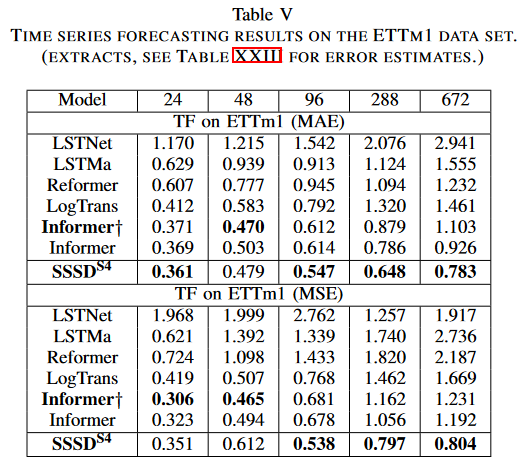
实验结果再次证实了^SSSDS4 的稳健预测能力，尤其是对于条件时间步长的长跨度预测。在第一种情况下，^SSSDS4 在MAE方面优于其他基线，但在MSE方面接近Informer†的得分；在第二种情况下，^SSSDS4在短预测条件和目标长度方面与Informer和Informer†相当，但在其余三种情况下与其余基线相比，^SSSDS4明显减少了误差，例如，与最强的基线Informer相比，分别获得0.783和0.804的MAE和MSE，分别为0.926和1.192。

摘要

我们提出将具有长期依赖性的连续数据的新建模范式--结构化状态空间模型与当前最先进的生成式建模方法之一--扩散模型^SSSDS4相结合，只要输入通道的数量不至于太大，就可以用于各种缺失数据。在各种情况下，发现它能提高现有最先进的完成度在各种数据集上的性能，在暂停缺失和预测情况下的性能尤其高。特别是，我们已经展示了可以用肉眼看到的完成质量的质的改善的例子。所提出的技术对时间序列领域的生成模型非常有前景，为建立以不同类型信息为条件的生成模型提供了可能，从全局标签到语义分区掩码等局部信息，从而实现了广泛的进一步下游应用。

• 
• 
• 

与本文相关的类别

• 论文
• 时间序列
• 时间序列
• 扩散模型