[Double Descent] Why Are "large Models" And "large Data Sets" Important?

3 main points

✔️ Double Descent is a phenomenon in which an error that increases due to overlearning turns into a decrease due to further learning.
✔️ Double Descent occurs when the model is increased in size, and the same phenomenon was observed for epoch numbers.
✔️ In order to discuss whether Double Descent occurs or not, a new measure called effective model complexity was created.

Deep Double Descent: Where Bigger Models and More Data Hurt
written by Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever
(Submitted on 4 Dec 2019)
Comments: G.K. and Y.B. contributed equally
Subjects: Machine Learning (cs.LG); Computer Vision and Pattern Recognition (cs.CV); Neural and Evolutionary Computing (cs.NE); Machine Learning (stat.ML)

code：  

The images used in this article are from the paper, the introductory slides, or were created based on them.

Introduction

There is a concept in statistical learning theory called the bias-variance trade-off (bias-variance trade-off). It means that there is a choice between bias and variance, but another way of saying this is that a model cannot be too simple and cannot be too complex.

If the model has too few parameters, it cannot cope with patterns in the data and errors will occur. This is called "large bias. Conversely, if there are too many parameters, the model fits too well to the training data and cannot handle the test data. This is called "large variance. In other words, bias-variance trade-off points out that there is an optimal model size for a certain data (task).

This has been said in classical statistical machine learning and was said to hold true for neural networks as well. However, this paper points out that in recent deep learning, this tradeoff does not always hold true.

If the tradeoff is correct, then as we continue to increase the model size for a given task, the performance of the model should decrease because of increased variance (overlearning). And in many cases, this is true. However, the authors further increased the size of the model. The error that had increased due to overlearning began to decrease again. This phenomenon is Double Descent.

This is said to have shown that "the bigger the model, the better," and gave birth to today's trend of "punching with power, not logic," and started the global competition for GPUs.

Double Descent

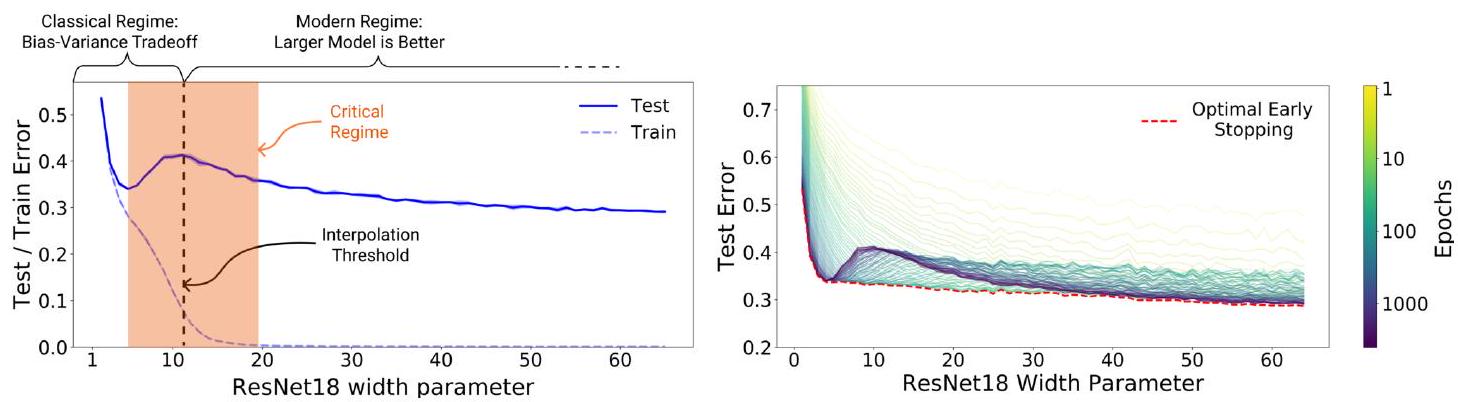
Let's look at Double Descent in the left figure.

The vertical axis is the error and the horizontal axis is the number of parameters. According to the bias-dispersion tradeoff, too many parameters increase the error. The solid blue line in the left panel shows that the error does indeed increase when the number of parameters is around 5. However, the error decreases when the number of parameters is further increased to around 10. This is the Double Descent phenomenon. Incidentally, the dashed line is training data, so the error is monotonically decreasing (overlearning).

Now that we know that the double-descent phenomenon occurs, we may be wondering how far the error will fall. This is illustrated in the figure on the right. The vertical and horizontal axes are the same as in the left figure, but they are color-coded according to the number of epochs. Looking at the light-colored areas (yellow to yellow-green), it appears that no double-descent occurred in the first place. The green area (100 epochs) shows Double Descent, and the blue area (1000 epochs) shows the largest drop. In other words, for models of the same size, the larger the epoch number, the smaller the error tends to be.

In other words, we can simply conclude that it is better to train a large model many times. It is important to note the red dashed line (Early Stopping). Although we can conclude from the figure on the right that it is better to train a large model many times, we can also see that it is possible to obtain the state with the smallest error more quickly by using Early Stopping. It shows that the best results can be obtained if the training is stopped at the appropriate point.

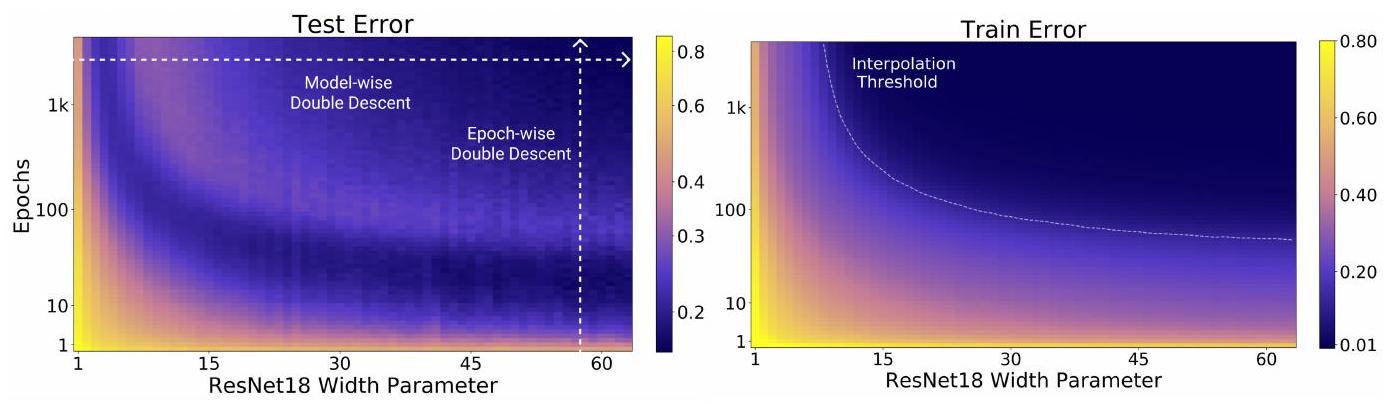
This figure shows the Double Descent in a different way. The horizontal axis remains the same as the number of parameters, but the vertical axis is now the number of epochs. The color indicates the error. In other words, the striped pattern (the same color appears) as shown in the left figure indicates that the error is going up and down, and Double Descent is expressed in a different way.

Experiments and Conclusions

In this paper, the conditions under which Double Descent occurs were examined in three experiments: "variable model parameters," "variable number of epochs," and "variable training samples.

The models used were ResNet18, a standard CNN, and Transformer, and the datasets were CIFAR-10, CIFAR-100, IWSLT'14, and WMT'14. The dataset and model combinations used in the experiments are as follows

Model-wise Double Descent by Model Size

As indicated in the introduction to Double Descent, Model-wise Double Descent is a phenomenon in which increasing the model size initially decreases the test error, beyond a certain point the test error increases, and further increasing the model size decreases the model error again.

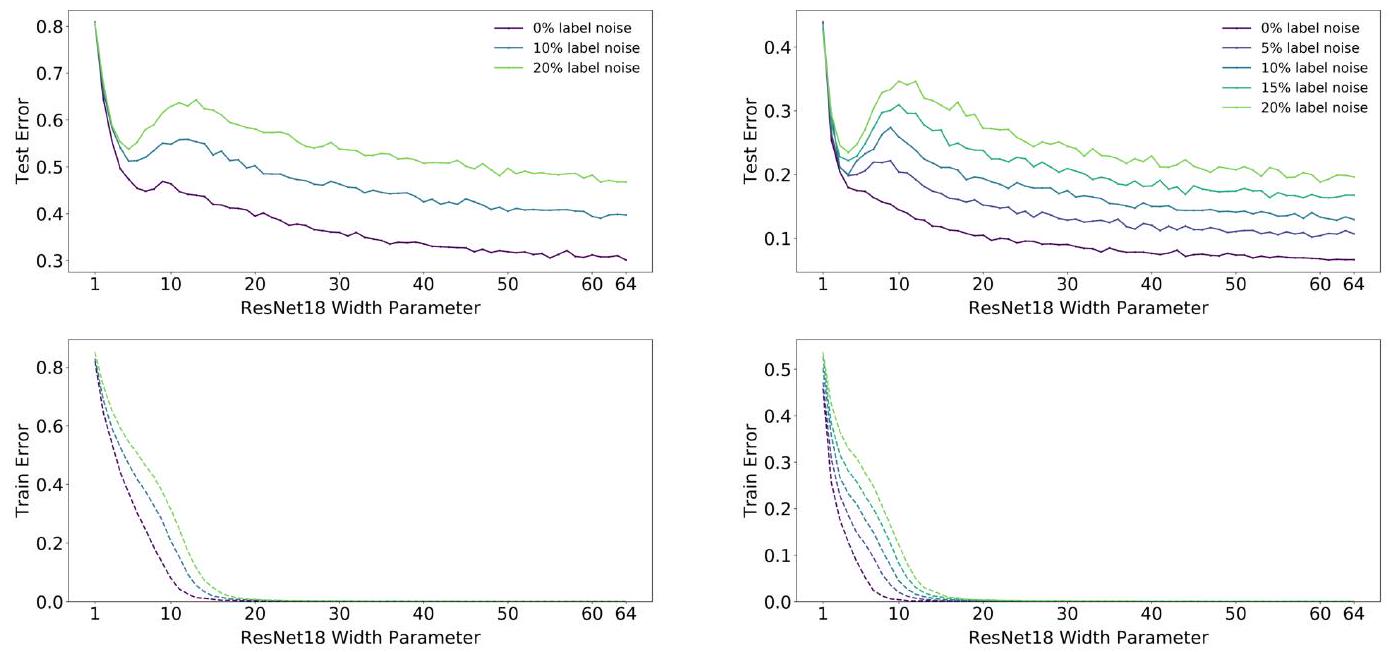
This figure shows a graph evaluating Double Descent using ResNet18 and CIFAR. The authors call the model size at which double descent occurs the interpolation point.

If you look closely here, do you see that the greater the label noise, the more the interpolation point shifts to the right? Supplementary information in the paper shows that the use of data augmentation and increasing the training sample also shift the interpolation point to the right. This means that label noise, data expansion, and increasing the training sample require larger model sizes.

Epoch-wise Double Descent

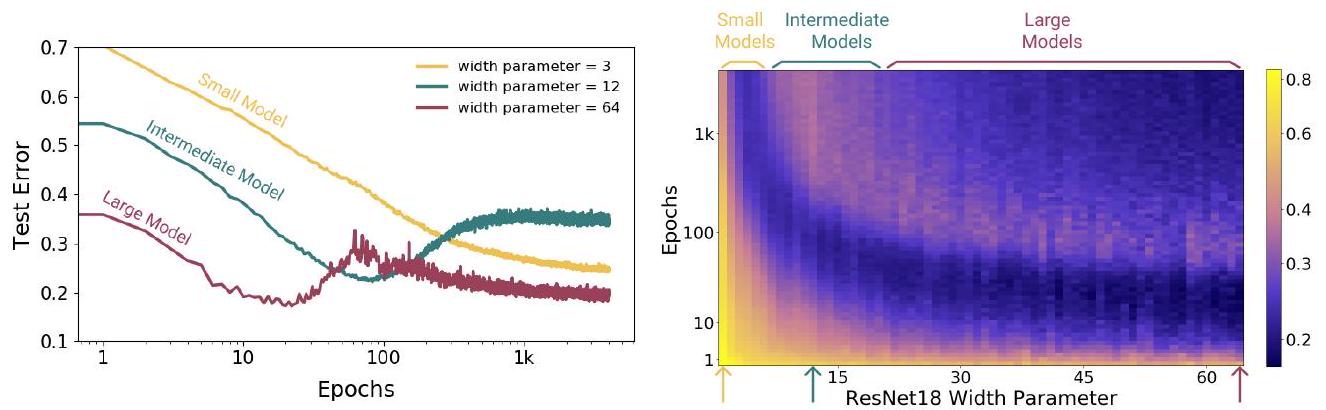This phenomenon is also explained in the introduction.

What is important to note in this figure is that a large model produces a Double Descent, while a small to medium sized model does not. More importantly, the medium-size model will stagnate with increasing test error.

Sample-wise non-monotonicity Sample-wise non-monotonicity

Sample non-monotonicity sample non-monotonicity is a counterintuitive phenomenon in which increasing training data does not necessarily improve performance on test data.

We have already seen Double Descent, but this phenomenon was referred to "increasing parameters" or "increasing the number of epochs". Sample Non-Monotonicity discusses how Double Descent occurs with respect to the "number of training data".

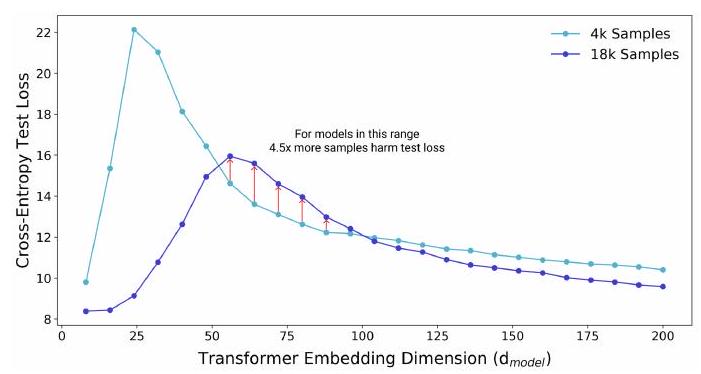
This figure shows the relationship between the size of the Transformer model (embedded dimension $d_{\text {model }}$) and the cross-entropy loss of the test data in the language translation task (IWSLT'14 German-to-English).

There are two models (4k, 18k). Intuitively, a model trained on 18k training data should always perform better than a model trained on 4k. However, at model sizes around 50~100, the 4k model shows less loss.

This suggests that the size of the training data set determines the appropriate model size. This points to sample non-monotonicity. Conversely, under certain conditions, it is possible for performance to decrease due to an increase in the training sample.

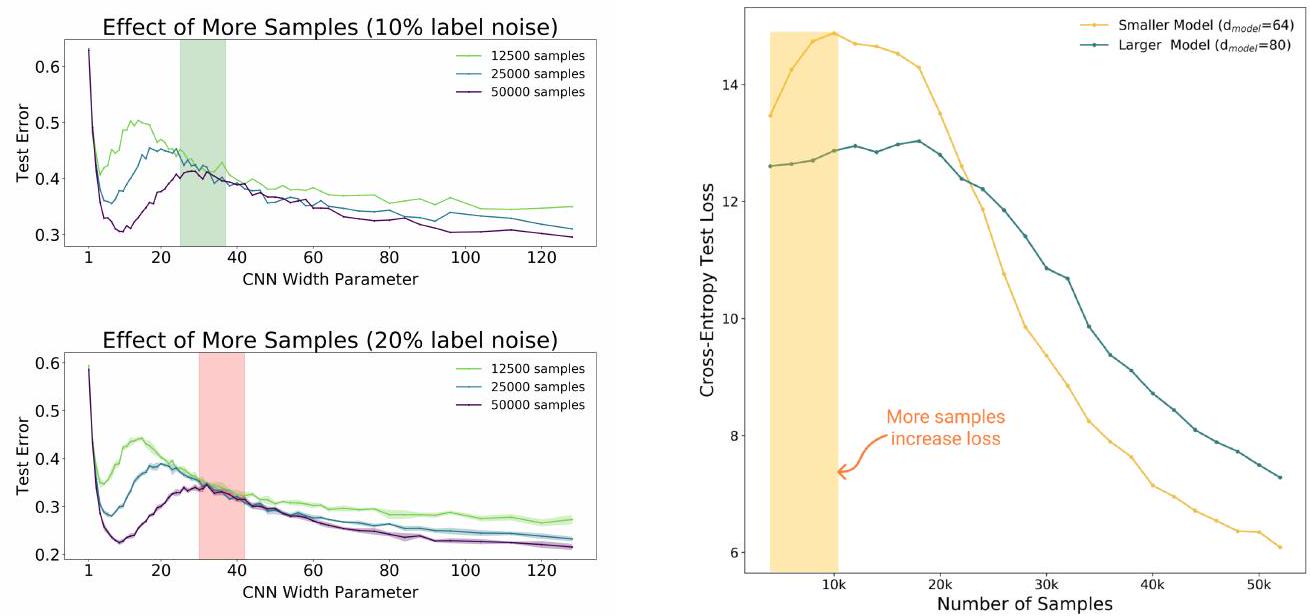
Here we experimented with a 5-layer CNN model and CIFAR-10. What is important to note in the left figure is that there is no significant difference in the test error for each model (125k, 250k, 500k) in the regions indicated by the green or red bands. This means that when the size of the model and the number of epochs are fixed, increasing the number of training samples by a factor of 4 may not improve the performance of the model. Strictly speaking, there are model sizes where increasing the number of training samples does not make much sense (see the band in the left figure).

To the right is an experiment using Transformer and IWSLT'14. Similar results occur here. Rather, in the area of the yellow band, the increase in the number of training samples is causing the performance of the model to deteriorate.

It indicates that simply increasing the model size or the amount of training data does not necessarily lead to better model performance, but may conversely lead to worse performance under certain conditions. This suggests that a balance between model size and training data size is important.

Effective Model Complexity

The authors proposed a measure called Effective Model Complexity (EMC) and formulated the conditions under which Double Descent occurs.

A training procedure $\mathcal{T}$ is defined as one that takes as input a set of labeled training samples $S=\left\{\left(x_{1}, y_{1}\right),\ldots,\left(x_{n}, y_{n}\right)\right\}$ and outputs a classifier $\ mathcal{T}(S)$ is defined as the output. The ECM for the procedure $\mathcal{T}$ (with the distribution as $\mathcal{D}$) is defined as the maximum number of samples $n$ for which the training error is approximately $0$.

$$\operatorname{EMC}_{\mathcal{D}, \epsilon}(\mathcal{T}):=\max \left\{n \mid \mathbb{E}_{S \sim \mathcal{D}^{n}}\left[\operatorname{ Error}_{S}(\mathcal{T}(S))\right] \leq \epsilon\right\}$$

The $\operatorname{Error}_{S}(M)$ represents the mean error of the model $M$ with $S$ training samples.

Hypothesis (General Double Descent Hypothesis)

Consider a natural data distribution $\mathcal{D}$, a neural network-based learning procedure $\mathcal{T}$, and a sufficiently small $\epsilon>0$, trained on $n$ samples from the distribution $\mathcal{D}$.

Under-parameterized regime

If $\mathrm{EMC}_{\mathcal{D}, \epsilon}(\mathcal{T})$ is sufficiently smaller than $n$, changes that increase the ECM will decrease the test error.

Over-parameterized regime over-parameterized regime

If $\mathrm{EMC}_{\mathcal{D}, \epsilon}(\mathcal{T})$ is sufficiently larger than $n$, changes that increase the ECM will decrease the test error.

Parameter proper region critically parameterized regime

If $\mathrm{EMC}_{\mathcal{D}, \epsilon}(\mathcal{T})$ is close to $n$, a change that increases the ECM will either decrease or increase the test error.

This hypothesis suggests that increasing model complexity is not generally a good thing, and that optimal performance depends on the balance between model complexity and the amount of training data.

Summary

In this paper, we show that for a given model and its training procedure, atypical behavior occurs when the number of training data is close to EMC. It is suggested that the generalized Double Descent Hypothesis holds regardless of the data set, model architecture, and training procedure. In particular, model-wise double descent showed that performance may be degraded when a smaller data set (decreasing ECM) is given for a larger model. Conversely, when the model size, number of datasets, and training procedure are appropriate, attempts to increase the number of datasets may in fact cause performance degradation.

This paper argues that "the number of data sets and the size of the model should be set appropriately," but paradoxically, a "larger model" and "larger number of data" will increase accuracy.I feel that this paper is important along with"Scaling Laws of LLM".

• 
• 
• 

Categories related to this article

• Article
• Machine Learning
• Double Descent
• Deep Learning
• Neural Network