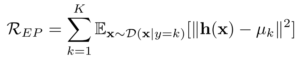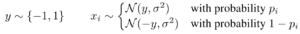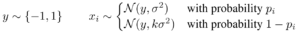データ分布の違いを攻略!情報ボトルネック法を活用した正則化手法Entropy Penalty
3つの要点
- 学習環境から分布のずれたテスト環境においても頑健なCNNモデルを学習
- 情報ボトルネック法を活用した正則化
- 事前情報なしに学習可能
独立同分布の仮定で作られたデータセットと現実環境
学習は順調に終わり、検証データで無事に効果は確認できた。しかし、テスト環境で思ったような性能が出ない…
機械学習の開発中、よくあることかもしれません。対処として、学習データが検証データにリークした可能性をチェックしたものの問題はなく、他のミスも特になさそう。だとしたら、テスト環境のデータ分布が、学習データの分布と違うのかもしれません。
機械学習に与えるデータセットは、「独立同分布 (i.i.d.)」が基本的な前提です。サンプルは全て同じ確率分布から得られ、互いに独立であると仮定されます。
例えば、犬・猫の画像で構成されるデータセットがあり、このデータセットを学習・検証・テストそれぞれのセットに分割することを考えてみます。
- 学習時・テスト時どちらにも含まれる犬・猫の比率が同じ ⇒ 同分布なのでOK、テスト時にも学習時と同様の性能が期待できる。
- 学習時には犬が多く、テスト時には猫が多くしたとき ⇒ 分布が異なり、前提条件が崩れている。テスト時に猫を犬と間違いやすくなると考えられる。
機械学習を実際に運用する現場を考えたとき、例えば猫の数が多く犬がほとんどいない地域でモデルを運用することもありえますので、後者のように分布がずれることは珍しいことではないでしょう。機械学習そのものとして学習と運用の環境が同じデータ分布であることを前提としているものの、現実的に分布が違うことは起こり得る問題です。
提案手法
「独立同分布」の前提が完全に成り立っていないケースでモデルを十分に汎化させるにはどうしたら良いのでしょうか。
一般的に学習で汎化を促すとき、下記のような方法が挙げられます。
- 正則化の各種手法を利用する。
- データ拡張(Augmentation)を使うかデータを追加して、データ分布をなるべく広げようとする。
この記事でご紹介する手法「Entropy Penalty」は前者の正則化として働き、データ分布のずれに頑健な学習を促します。
ただし通常「汎化させる」ことは、モデルの「過学習」を防ぐことを意味します。つまり学習した後、同じ分布を持つ検証セット、更にはテスト環境で十分な性能を発揮できることを目的とします。この手法では通常の汎化目的を超えて、テスト環境のデータ分布が学習時と異なる場合でも十分な性能が発揮できることを目的としており、そのための正則化手法ということになります。
とはいえ、あまりに違う分布を対象としているわけではありません。例えば犬/猫の画像のケースで説明すると、学習・検証セットは昼間の撮影画像で、テスト時に夜間の撮影画像を使った場合、これくらいのずれ方を対象としています。あくまで検出の対象(犬/猫)は入れ替わることがなく、データに含まれる周辺の特徴(昼間/夜間)がずれた場合、ということになります。
分布のずれたテスト環境にどうやって汎化させるか
先程の例のように、画像の中でも犬/猫の特徴を学習させて、それ以外の特徴は無視するようにしたいのです。
そのための枠組みとして、情報ボトルネック(IB)法を使うことを提案しています。以下、論文の数式を読み解いていきますが、簡単にはこのようになりますす。
- Entropy Penalty正則化は、CNNモデルの第一層が出力する潜在表現のばらつきを抑える働きをする。
- ミニバッチ単位で、ばらつきを抑える正則化のロスを計算する。
- バラつかない=クラスの特徴を捉えた良い表現になっていて、バラつく=背景のような望ましくないものが表現に含まれる、という考えに基づく。
このIB法を最小化する目的関数はこのようになります。
X、Yはそれぞれ入力、出力(多くの場合ラベル)。fθはパラメーターθの(決定論的)モデル、βはハイパーパラメーターで、I(・,・)は相互情報量を表します。
右辺を見てみると、
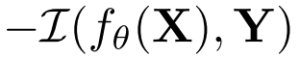 は通常の学習目的、モデルの出力とターゲットを一致させたい(=モデルの出力とターゲットの相互情報量を大きくしたい)。
は通常の学習目的、モデルの出力とターゲットを一致させたい(=モデルの出力とターゲットの相互情報量を大きくしたい)。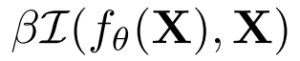 はモデル出力と入力の相互情報量をなるべく小さくしたい目的。
はモデル出力と入力の相互情報量をなるべく小さくしたい目的。
後者がこの手法のポイントになります。
ここで相互情報量とは、不確実さ(≒エントロピー)の減少量というこの説明(5.相互情報量)が的確です。前者の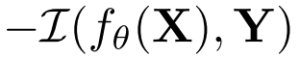 はラベルYにモデルが正解となるようにしたいので、言い換えるとモデルの出力が不確実になることを減らしたい、ということになります。
はラベルYにモデルが正解となるようにしたいので、言い換えるとモデルの出力が不確実になることを減らしたい、ということになります。
ところが後者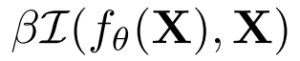 はどうでしょうか。ここで相互情報量をエントロピーに展開すると理解しやすくなります。エントロピー(平均情報量)は、ここでは単純に情報量と捉えてみます。犬の例でいうと体の色や形、四足であることなど、特徴づける情報が多岐にわたります。情報量が大きいfθ(X)は、入力画像Xの犬だけでなく背景の色や形まで含んでしまうでしょう。逆に犬であることを最小限で表すfθ(X)は、犬の情報だけを表すよう情報量が小さくなるでしょう。相互情報量はこのエントロピーH(・)で、
はどうでしょうか。ここで相互情報量をエントロピーに展開すると理解しやすくなります。エントロピー(平均情報量)は、ここでは単純に情報量と捉えてみます。犬の例でいうと体の色や形、四足であることなど、特徴づける情報が多岐にわたります。情報量が大きいfθ(X)は、入力画像Xの犬だけでなく背景の色や形まで含んでしまうでしょう。逆に犬であることを最小限で表すfθ(X)は、犬の情報だけを表すよう情報量が小さくなるでしょう。相互情報量はこのエントロピーH(・)で、
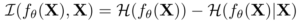
と表されます。入力画像をモデルの潜在表現に変換したときの平均情報量H(fθ(X))から、特定の入力画像Xの潜在表現の平均情報量H(fθ(X)|X)を引く、そのI(fθ(X),X)が小さくなってほしい。つまりXに関わらずfθ(X)の表す情報量が変わらない、fθ(X)は少ない情報量でXを表現させたい、ということに解釈できそうです。
このように平均情報量(エントロピー)でブレークダウンし、定数項を除くことで、Entropy Penalty正則化がこのように定義されます。
右辺を再び見ていくと、前者は最尤法のロスそのもので、後者はモデルが学習した表現の平均情報量ということになります。単に学習することに加えて、表現の情報量をできるだけ減らしたい、と解釈できます。
しかしこの式のままでは実際には扱えないので、fθ(X)をラベルYの学習データに限定します。
Cはθとは無関係にラベルYによって決める定数です。 更に仮定を追加して導いていきます。
- ここで
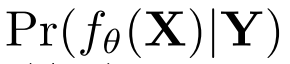 がラベルYに対するガウス分布と仮定すると、分散
がラベルYに対するガウス分布と仮定すると、分散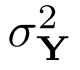 の閉形式
の閉形式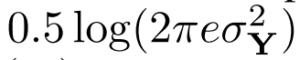 に簡単化できます。
に簡単化できます。
- また実際の深層学習に適用するとき、ネットワークのどの層の潜在表現を使って計算するのかを決める必要があります。このとき最終層ではなく、はじめの層から得た表現に適用する方が効果が大きいことがわかっています。
以上から、Entropy Penalty正則化の実装を下記のように導いて、サンプルのクラス別に分散を計算する実装としています。
ここで h(x)は最初の層の潜在表現、
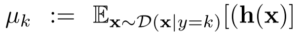
はその期待値、Dはデータ分布です。
さらに実際の学習を考慮して、期待値の計算はミニバッチでの平均で置き換えます。
人工的データセットでの分析
人工的に作り出した2つのデータセットを用いて有効性を分析しています。
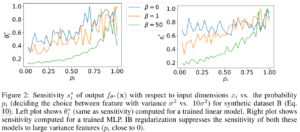
人工的データセットA 〜入力xの平均値が異なるケース
このデータセットでは、パラメータ p 次第で入力データの平均値が偏るデータを用意して分析します。
- p = 0または1に近い値では、出力との相関が強い入力データの分布となる。特徴量が頑健になる設定。
- p = 0.5に近い値では、出力と関係が薄く予測が困難な入力データ分布、特徴量が頑健ではなくなる。
このデータを使ったとき、どうなるかを見てみます。
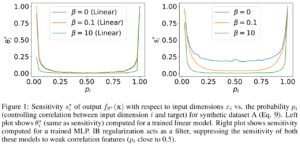
左は線形モデルで学習させたとき、右はMLPで学習させたときのグラフになります。
横軸はデータを生成するp、縦軸は入力データに対する出力の「感度」(線形モデルのときは重みθそのもの)。
特徴量の頑健さが損なわれている状況で(pが0.5に近いとき)、βを大きくするほど情報ボトルネックによる正則化が働く様子が示されています。
特にMLP(右)で感度が抑えられ、頑健ではない特徴量に依存しなくなっていることがわかります。
人工的データセットB 〜入力xの分散が異なるケース
今度は平均値ではなく、入力の分散の量が確率 p で決まるようなデータを用意します。pが小さいほど入力データの分散が大きく、pが大きいほど入力データの分散が小さくなるデータです。
この結果は、情報ボトルネックによる正則化を使うほど(βが大きいほど)、分散の大きな入力に左右されなくなることを示しています。
分散の大きな入力は頑健な特徴ではなく、テスト時に分布がずれたときモデルの推論に大きな悪影響を与えられると考えられます。
情報ボトルネックの正則化では、分散の大きな入力への感度を下げることができます。
分布のずれたデータでの実験
画像データを使った実験では、データセットとしてC-MNIST(カラー化したMNIST)、MNIST-M(背景付与などを施したMNIST)、SVHN、標準の(MNIST)が使われています。
C-MNISTの場合、学習セットに対してテストセットは配色が全く異なります。決まった色でモデルを学習させ、テスト時にはランダムな配色のサンプルを使います。
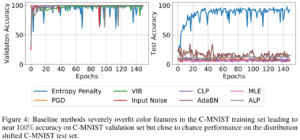
このデータを学習したとき、学習の進捗に伴う精度がどう変化したのかを下記のグラフで示しています(左: 検証時、右: テスト時)。
想定通り、Entropy Penalty以外の全ての方式は、検証セットで高い精度が出ているにも関わらず、テストセットでは全く精度が出ていません。
テストのランダムな配色に関わらずEntropy Penaltyは精度を確保できており、頑健でない特徴(色)に左右されないように学習が実現できていることがわかります。
テストセットだけの結果を見た結果は以下の通りです。
特に右側の表では、C-MNISTをEntropy Penaltyで学習したモデルが、他のMNIST系だけでなくSVHNへも汎化している例が示されています。
上からMNIST、SVHN、MNIST-Mのデータ例。
C-MNISTで学習させたモデルで、これらのデータに汎化しています。
Batch Normalizationとの関係
実験ではResNet-56を使っていますが、重要な実験条件としてBatch Normalization(BN)を使用していないということが挙げられます。
BNは正規化に必要な統計量を予め学習時に計算し、テスト時には保持された値を利用して正規化します。
このためテストでデータ分布がズレると、保持された値がもはや不適切になることが直感的にわかります。
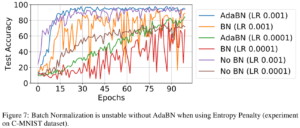
実際に実験で確かめられています。BNを使ったとき、No BNで使わなかったとき、テストデータから適応させるAdaBNを使ったときの結果です。
BNを使うオレンジや赤の結果のように、非常に不安定になることがわかります。
まとめ
情報ボトルネック法を使った正則化の手法Entropy Penaltyをここまでご紹介しました。
Entropy Penalty正則化により、学習時とテスト時でデータ分布がずれてしまうようなケースでも頑健なモデルを学習させられることが実験で示されました。
C-MNISTで色付きの文字画像認識を学習したモデルが、他の複数の文字データセットで汎化していることも実験で示されました。
しかし、Batch Normalizationとの共存が難しいことも分かっています。深層学習モデルにはBNが現実的に不可欠な状況を考えると、この手法を応用できる機会は今のところ限られていると解釈すべきかもしれません。
最後に、 独立同分布の仮定に基づくプラクティスに一石を投じて論文は締めくくっています。
“Eearly Stoppingとハイパーパラメータの選択に検証セットを使用する従来の慣習は、トレーニング/検証/テストセットが独立同分布からサンプリングされるという仮定に基づいています(Arlot et al., 2010)。しかしながら、データ分布から外れたテストセットで評価することが目標である場合には、Early Stoppingやハイパーパラメータ選択の方法は明確ではありません。これは、頑健ではない特徴が学習セットと検証セットの間で共有されるため、検証セットでの高いパフォーマンスはテストセットでも同様になることを必ずしも意味しないためです。このトピックには今後さらに注意が必要です。”


-
- 製造業を中心に数々の製品ソフトウェア設計を成功させたバックグラウンドを持ち、ディープラーニングをインパクトに変える研究開発をオープンに推進。ご相談はTwitterアカウントへのDMにてお願いします。
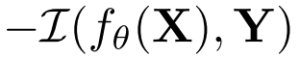 は通常の学習目的、モデルの出力とターゲットを一致させたい(=モデルの出力とターゲットの相互情報量を大きくしたい)。
は通常の学習目的、モデルの出力とターゲットを一致させたい(=モデルの出力とターゲットの相互情報量を大きくしたい)。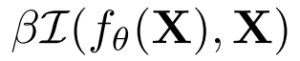 はモデル出力と入力の相互情報量をなるべく小さくしたい目的。
はモデル出力と入力の相互情報量をなるべく小さくしたい目的。![]() はラベルYにモデルが正解となるようにしたいので、言い換えるとモデルの出力が不確実になることを減らしたい、ということになります。
はラベルYにモデルが正解となるようにしたいので、言い換えるとモデルの出力が不確実になることを減らしたい、ということになります。![]() はどうでしょうか。ここで相互情報量をエントロピーに展開すると理解しやすくなります。エントロピー(平均情報量)は、ここでは単純に情報量と捉えてみます。犬の例でいうと体の色や形、四足であることなど、特徴づける情報が多岐にわたります。情報量が大きいfθ(X)は、入力画像Xの犬だけでなく背景の色や形まで含んでしまうでしょう。逆に犬であることを最小限で表すfθ(X)は、犬の情報だけを表すよう情報量が小さくなるでしょう。相互情報量はこのエントロピーH(・)で、
はどうでしょうか。ここで相互情報量をエントロピーに展開すると理解しやすくなります。エントロピー(平均情報量)は、ここでは単純に情報量と捉えてみます。犬の例でいうと体の色や形、四足であることなど、特徴づける情報が多岐にわたります。情報量が大きいfθ(X)は、入力画像Xの犬だけでなく背景の色や形まで含んでしまうでしょう。逆に犬であることを最小限で表すfθ(X)は、犬の情報だけを表すよう情報量が小さくなるでしょう。相互情報量はこのエントロピーH(・)で、![]()
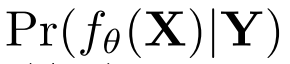 がラベルYに対するガウス分布と仮定すると、分散
がラベルYに対するガウス分布と仮定すると、分散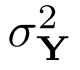 の閉形式
の閉形式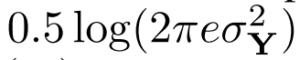 に簡単化できます。
に簡単化できます。