[双重后裔] 为什么 "大模型 "和 "大数据集 "很重要？

神经网络 25/07/2024

三个要点

✔️ 双倍下降是指由于过度学习而增加的误差随着进一步学习转为减少的现象。
✔️ 当模型的规模增大时，就会出现双倍下降现象，而且在历时数方面也观察到了同样的现象。
✔️ 为了讨论是否会出现双下降现象，我们创建了一种新的测量方法，称为有效模型复杂度。

Deep Double Descent: Where Bigger Models and More Data Hurt
written by Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever
(Submitted on 4 Dec 2019)
Comments: G.K. and Y.B. contributed equally
Subjects: Machine Learning (cs.LG); Computer Vision and Pattern Recognition (cs.CV); Neural and Evolutionary Computing (cs.NE); Machine Learning (stat.ML)

code：

本文所使用的图片要么来自论文、介绍性幻灯片，要么是参考这些图片制作的。

介绍

统计学习理论中有一个概念叫做 "偏差-方差权衡"（bias-variance trade-off）。它的意思是在偏差和方差之间进行选择，换一种说法就是模型不能太简单，也不能太复杂。

如果模型参数太少，就无法应对数据中的模式，就会出现误差。这就是所谓的 "大偏差"。相反，如果参数过多，模型就会与训练数据拟合得太好，而无法应对测试数据。这就是所谓的 "大方差"。换句话说，偏差-方差权衡表明，对于某些数据（任务），存在一个最佳模型大小。

这在经典的统计机器学习中已有论述，在神经网络中也同样成立。然而，本文指出，在最新的深度学习中，这种权衡并不总是成立的。

如果权衡是正确的，那么如果在一项任务中不断增加模型的大小，模型的性能就会因为方差增大（过度学习所致）而下降。而在很多情况下，事实的确如此。然而，作者进一步增大了模型的规模。他们发现，由于过度学习而增加的误差又开始下降。这种现象就是双下降。

据说，这表明 "模型越大越好"，催生了今天 "用力量而不是逻辑打拳 "的趋势，以及全球 GPU 大战。

双人后裔（双人后裔）

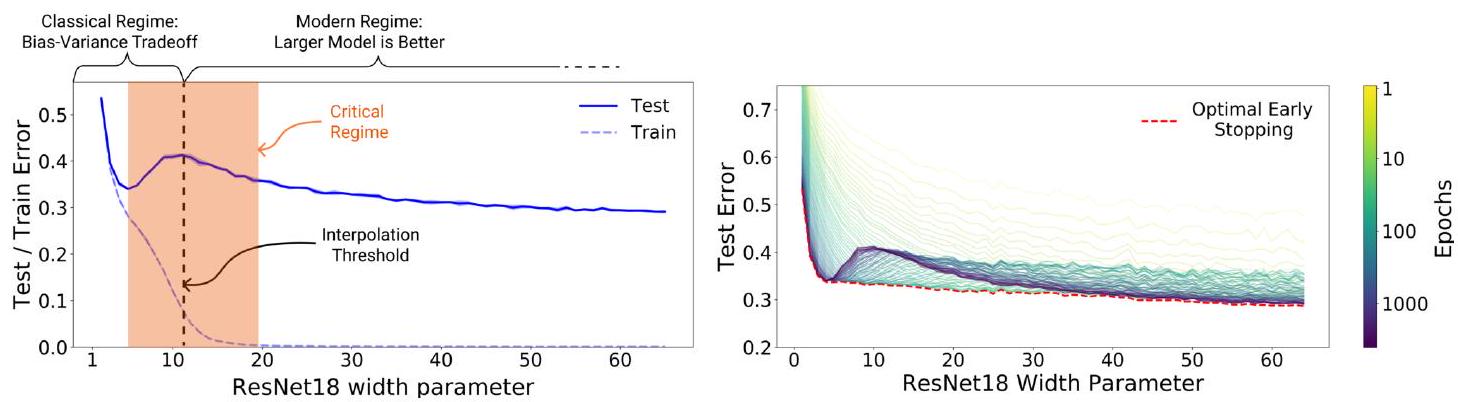
请看左图中的 "双下降"。

纵轴为误差，横轴为参数数。根据偏差-分散权衡原理，如果参数数过多，误差就会增大，对吗？左图中的蓝色实线表明，当参数数为 5 左右时，误差确实会增大。不过，我们也可以看到，当参数数进一步增加时，误差会在 10 左右减小。这就是双下降现象。顺便提一下，虚线是训练数据，因此误差是单调递减的（过度训练）。

既然我们知道会出现双重下降现象，那么我们可能会想知道误差会下降到什么程度。右图对此进行了说明。纵轴和横轴与左图相同，但按年代编号用颜色标示。从浅色区域（黄色到黄绿色）来看，似乎最初并没有出现 "双降 "现象。绿色附近（100 个纪元）出现了双下降，蓝色附近（1000 个纪元）下降幅度最大。这说明，对于相同大小的模型，越大的历元误差越小。

换句话说，可以得出一个简单的结论："最好对大型模型进行多次训练"。请注意红色虚线（早期停止）。从右图中，我们可以得出结论："最好多次训练大型模型"，但我们也可以看到，使用 "早期停止 "可以更快地获得误差最小的状态。这表明，如果在适当的时候停止训练，就能获得最佳结果。

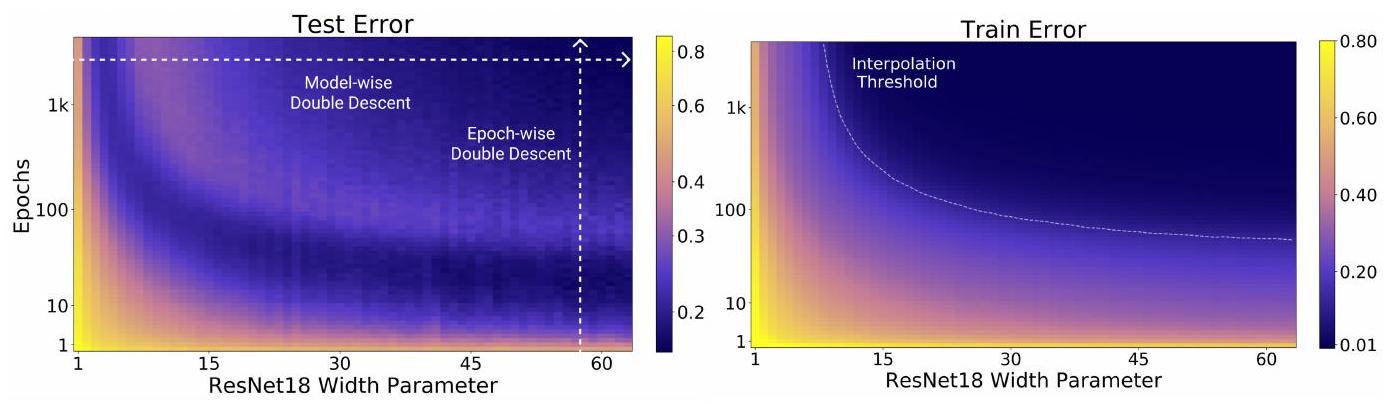
该图以不同的方式显示了之前的双倍下降。横轴与参数数相同，但纵轴现在是历时数。颜色表示误差。换句话说，左图中的条纹外观（出现相同的颜色）表明误差在上升和下降，这以不同的方式表示了双倍下降。

实验和结论

本文通过 "可变模型参数"、"可变历元数 "和 "可变训练样本 "这三个实验，研究了发生 "双下降 "的条件。

使用的模型是 ResNet18、标准 CNN 和 Transformer，数据集是 CIFAR-10、CIFAR-100、IWSLT'14 和 WMT'14。实验中使用的数据集和模型组合为

模型双降模型双降

正如 "双下降 "介绍中所述，"模型双下降 "是一种现象，即增加模型大小最初会减小测试误差，超过一定程度后测试误差会增大，而进一步增加模型大小又会减小模型误差。

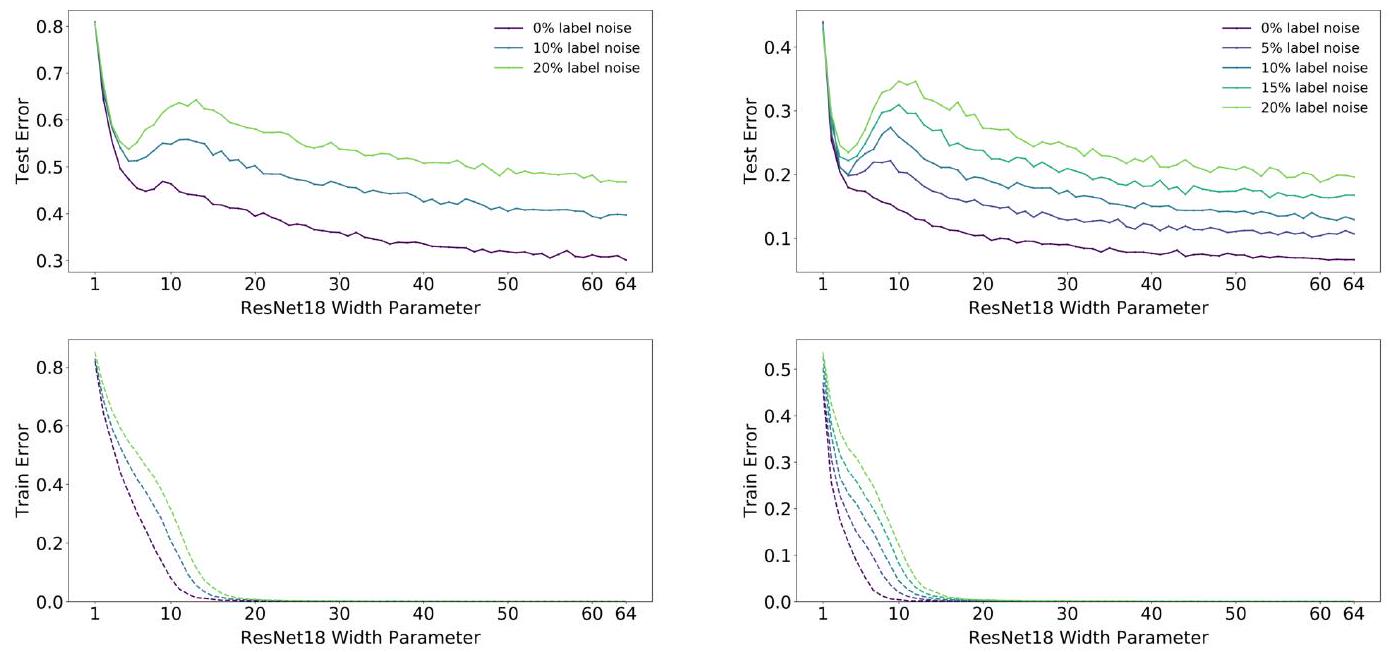
本图是使用 ResNet18 和 CIFAR 评估双下降的图表。无论标签噪声（给出错误的正确答案）的程度如何，在一定的模型大小下都会出现双下降现象；作者将出现双下降现象的模型大小称为插值点。

仔细观察这里，你是否发现随着标签噪声的增加，插值点也在向右移动？论文的补充信息显示，使用数据扩展和增加训练样本也会使插值点向右移动。这意味着标签噪声、数据扩展和训练样本的增加需要更大的模型规模。

时代性的双重后裔时代性的双重后裔

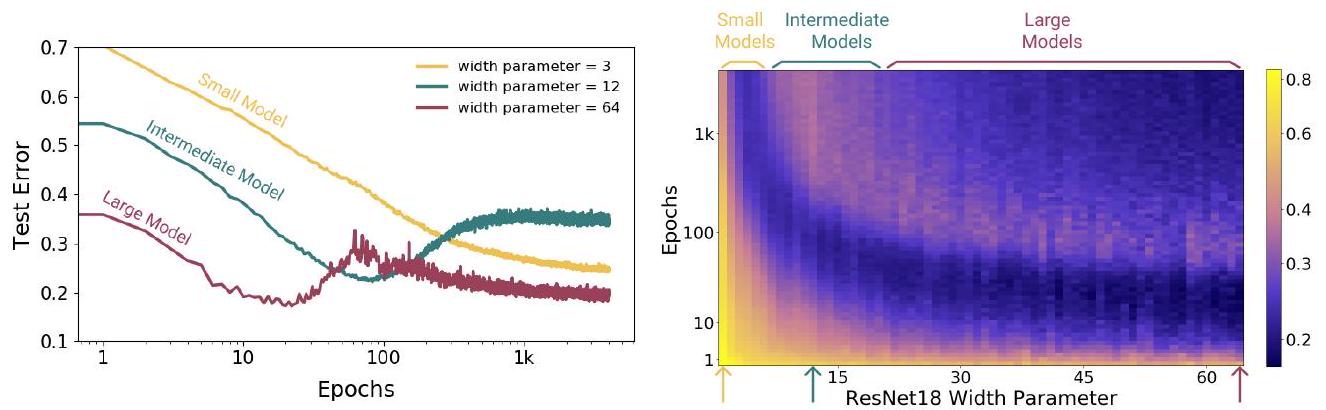导言中也解释了这一现象。

从图中可以看出，大型模型会产生 "双下降 "现象，而中小型模型则不会。更重要的是，随着测试误差的增加，中型模型的学习会停滞不前。

抽样非单调性抽样非单调性抽样非单调性抽样非单调性

样本非单调性样本非单调性是一种违背直觉的现象，即增加训练数据并不一定能提高测试数据的性能。

我们已经看到过双倍下降现象，但这种现象指的是 "增加参数 "和 "增加历元数"。样本非单调性讨论的是 "训练数据的数量 "是否会导致 "双下降"。

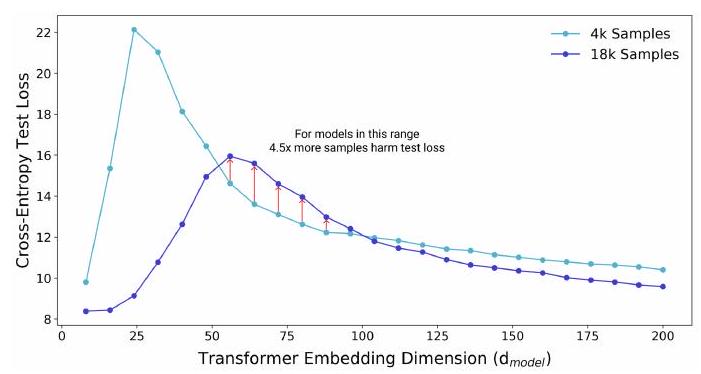
该图显示了 Transformer 模型的大小（嵌入维度 $d_{\text {model }}$）与语言翻译任务（IWSLT'14 德语到英语）中测试数据的交叉熵损失之间的关系。

有两种模型（4k、18k）可供选择。根据直觉，在 18k 训练数据上训练出来的模型应该总是比在 4k 训练数据上训练出来的模型表现更好。不过，在模型规模约为 50-100 时，4k 模型的损失较小。

这表明，训练数据集的大小决定了适当模型的大小。这说明了样本的非单调性。相反，在某些条件下，由于训练样本的增加，性能可能会降低。

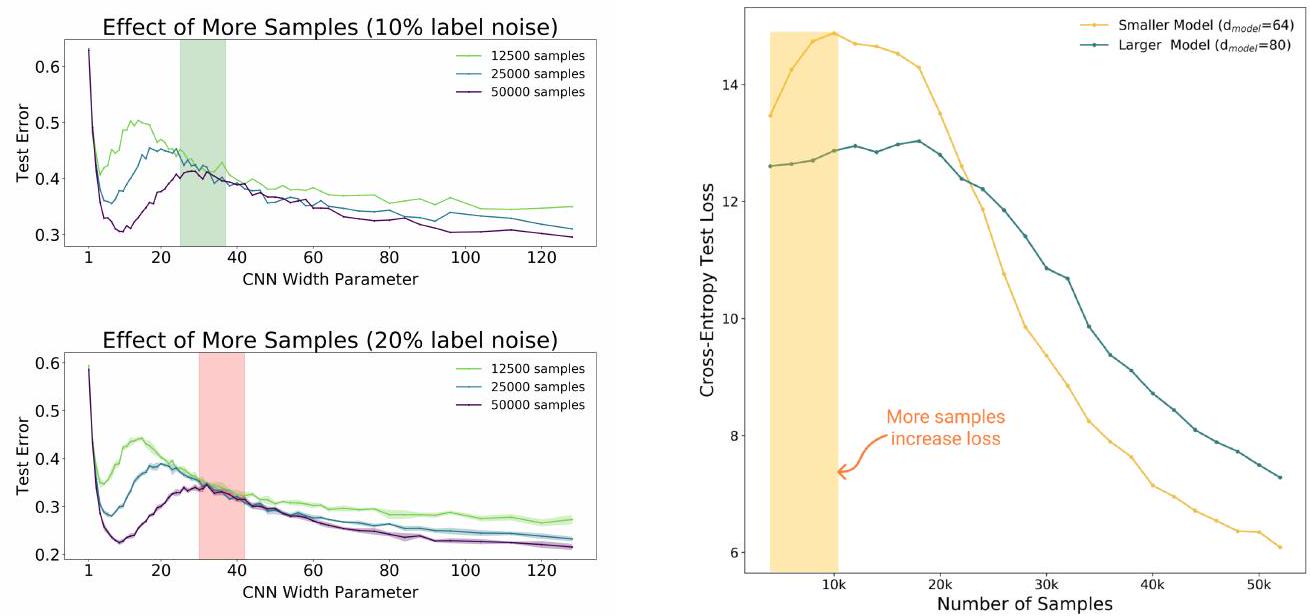
在此，我们使用五层 CNN 模型和 CIFAR-10 进行了实验。左图中值得注意的是，在绿色或红色条带所指示的区域内，每个模型（125k、250k、500k）的测试误差没有明显差异。这意味着，在模型大小和历时次数固定的情况下，将训练样本数量增加四倍也未必能提高模型的性能。严格来说，在某些模型规模下，增加训练样本的数量并没有太大意义（左图中的带状区域）。

右图是使用 Transformer 和 IWSLT'14 进行的实验。这里也出现了类似的结果。相反，在黄色区域，训练样本数量的增加导致模型性能下降。

这表明，简单地增加模型大小或训练数据量并不一定会提高模型性能，在某些条件下反而可能导致性能下降。这表明，模型大小和训练数据量之间的平衡非常重要。

有效模型复杂性有效模型复杂性

作者提出了一种名为 "有效模型复杂性"（EMC）的测量方法，并制定了发生 "双下降 "的条件。

训练过程 $\mathcal{T}$ 被定义为将一个已标记的训练样本集 $S=\left\{left(x_{1}, y_{1}\right),\ldots,\left(x_{n}, y_{n}\right)\right\}$ 作为输入，并将一个分类器 $\mathcal{T}(S)$ 定义为输出。mathcal{T}(S)$ 被定义为输出。程序 $\mathcal{T}$ 的 ECM（分布为 $\mathcal{D}$）被定义为训练误差近似为 $0$ 的最大样本数 $n$。

$$\operatorname{EMC}_{\mathcal{D}, \epsilon}(\mathcal{T}):=\max \left\{n \mid \mathbb{E}_{S \sim \mathcal{D}^{n}} 左[\operatorname{.Error}_{S}(\mathcal{T}(S))\right] \leq \epsilon\right}$$

操作名{错误}_{S}(M)$ 表示模型 $M$ 在 $S$ 训练样本下的平均误差。

假说（一般双重后裔假说）

考虑自然数据分布 $/mathcal{D}$、基于神经网络的学习程序 $/mathcal{T}$、在足够小的 $epsilon>0$ 条件下对分布 $/mathcal{D}$ 中的 $n$ 样本进行训练的情况。

欠参数制度欠参数制度

如果 $\mathrm{EMC}_{mathcal{D}, \epsilon}(\mathcal{T})$足够小于 $n$，那么增加 ECM 的变化将减少测试误差。

过参数化系统过参数化系统

如果 $\mathrm{EMC}_{mathcal{D}, \epsilon}(\mathcal{T})$足够大于 $n$，那么增加 ECM 的变化将减少测试误差。

参数适当的制度关键参数化的制度

如果 $\mathrm{EMC}_{mathcal{D}, \epsilon}(\mathcal{T})$接近 $n$，那么增加 ECM 的变化要么会减少测试误差，要么会增加测试误差。

这一假设表明，增加模型的复杂度通常不是一件好事，最佳性能取决于模型复杂度和训练数据量之间的平衡。

摘要

本文表明，对于给定的模型及其训练过程，当训练数据的数量接近 EMC 时，就会出现非典型行为。本文认为，广义双下降假说与数据集、模型结构和训练过程无关。特别是，模型双下降表明，当为较大模型提供较小的数据集（ECM 越小）时，性能可能会下降。相反，当模型大小、数据集数量和训练过程都合适时，试图增加数据集数量反而会导致性能下降。

本文的论点是 "应适当设定数据集的数量和模型的大小"，但矛盾的是，"更大的模型 "和 "更多的数据 "会提高准确性。我认为这篇论文是与《LLM 的缩放定律》并列的一篇重要文献。