
教師あり学習の精度を超えた!?相互情報量の最大化による教師なし学習手法IICの登場!
3つの要点
✔️相互情報量を最大化する枠組みでニューラルネットを学習する教師なし学習手法IICの提案
✔️予測値をそのまま出力するニューラルネットを学習可能であるため、クラスタリングが不要
✔️従来の教師なし学習手法の「クラスタが一つにまとまってしまう問題」および「ノイズに弱いという問題」を解決
Invariant Information Clustering for Unsupervised Image Classification and Segmentation
written by Xu Ji et.al
(Submitted on 22 Aug 2019)
subjects : Computer Vision and Pattern Recognition (cs.CV); Machine Learning (cs.LG)
はじめに
近年、様々な場面において、深層学習手法が使用され始めています。これは深層学習手法は、非常に優れた性能を発揮するからです。しかし、深層学習モデルを学習するには大量のラベル付きデータが必要であり、これが深層学習手法の実応用を制限しています。
そういった背景があり、ラベル情報を必要としない教師なし学習が注目を集めています。教師なし学習では、データから良い特徴量を得ることが目的です。例えば、クラス分類を行いたい時は同じクラスに属するデータはまとまっていて、異なるクラスに属するサンプルは離れていると良い特徴量だと言えます。
しかし、従来の教師なし学習には二つの大きな問題を抱えています。一つは特徴量を得て、それを元にクラスタリングを行う際に、たびたびクラスタが一つにまとまってしまう、または本来あるべきクラスタが消えてしまうという問題が指摘されています。また、二つ目の問題点は学習データにノイズを含んだデータがあった場合、良い特徴量を得ることができないという問題です。
上記に述べた問題点を解消する手法として、本論文では相互情報量を最大化することで、ネットワークを学習させる手法(IIC)を提案しています。後の章で相互情報量については簡単に紹介しますが、これを用いることで二つの問題を解決することが可能となります。以下の図は、IICによる画像分類とセグメンテーションの結果を可視化したものです。

図1. IICによる画像分類とセグメンテーション結果の可視化
本論文では、IICを用いて画像分類タスクとセグメンテーションタスクの実験を行い、どちらのタスクでもSOTAを出しています。また、半教師あり学習にIICを適応した場合、教師あり学習の精度を超えるという結果を出しています。
なお、IICは汎用的な手法であり、データの相互情報量が計算できれば、様々なタスクに使用することができることも大きなメリットです。
相互情報量の最大化による利点
ここでは、簡単に相互情報量について紹介し、相互情報量の最大化による学習の利点を説明します。
まず相互情報量はある確率分布のペア(z, z’)に対して、以下のように定義されます。本論文では、(z, z’)は入力(x, x’)に対するニューラルネット$Φ$の出力である確率分布を表しています。つまり$z = Φ(x)$です。
$I(z,z’) = H(z) – H(z|z’)$
ここで$H(z)$はzに対するエントロピー、$H(z|z’)$はz’が与えられた元での条件付きエントロピーを表しています。エントロピーとは、情報の曖昧さを表す指標であり、情報が曖昧であるほど大きい値をとります。(一様分布のとき最大となり、ある一点で1をとる確率分布のとき0となります)
IICでは、ニューラルネットΦを学習することによって、相互情報量の最大化を目指します。これは相互情報量の第一項目を大きく、かつ、第二項目を小さくするということに他なりません。
まず、第一項目である$H(z)$を大きくするということは、zが一様分布に近づくように学習が進むことを意味しており、これによって、一つのクラスタにまとまるということがなくなります。しかし、$H(z)$の最大化だけでは、zの分布は一様分布となってしまい、意味のない出力となってしまいます。ここで、第二項目である$H(z|z’)$を小さくすることにより、出力がある程度、意味あるものとなるように学習が進みます。

図2. MNISTデータにおけるIICの学習過程
図2は、MNISTデータセットにおけるIICの学習過程を表した図です。左から右に行くにしたがって、学習が進んで行きます。最初特徴量はまとまっていますが、学習が進むにつれ、他のクラスと分かれていく様子が見られます。
また、zとz’が似ていれば、第二項の条件付きエントロピーは小さくなります。これは、zに似たz’を与えてしまえば、曖昧さが減少するからです。つまり、xとx’の共通の部分に着目して予測値を出力するように、ネットワークの学習が進みます。これにより、同じクラスに属するサンプルは同じ出力をする様にネットワークが学習されます。
提案手法
では、相互情報量の最大化の利点が分かったところで、提案手法であるIICについて説明します。IICは大きく分けて、以下の二つのステップで構成されています。
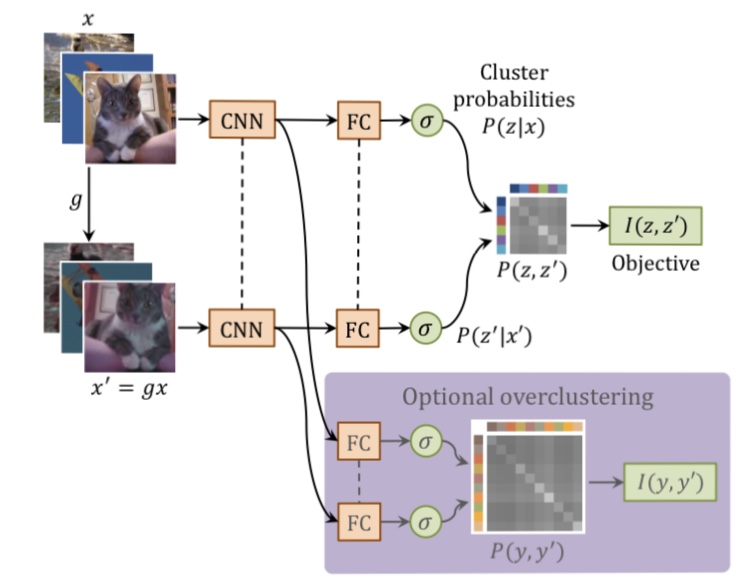
図3. IICの概要図
(1) データ$x$のペアとなる$x’$を$x$を元に生成する
(2) ニューラルネット$Φ$に$(x, x’)$を入力し出力$(z, z’)$を得て、$I(z, z’)$を最大化するようにネットワークを学習する
本論文では、IICを画像分類のタスクとセグメンテーションのタスクに適応しています。それぞれのタスクに対して、(1), (2)のステップを見ていきましょう。
画像分類タスク
画像分類タスクを行う場合、xのペアであるx’を生成するために、xを幾何学的に変形させたり、コントラストを変えたりしてx’を生成します。つまり、ある変換gを定義し、
$x’ = gx$
としたものがx’となります。このように自分自身を変化させたものとの相互情報量を最大化するように学習を行うことで、ノイズが加わったデータでも意味のある部分のみに着目できるようになります。
セグメンテーションタスク
セグメンテーションタスクでは、ピクセル毎に分類を行う必要があります。そして、あるピクセルとその近くにあるピクセル同士は空間的な相関を持ちます。
そこで、IICでは画像をパッチに分割し、あるパッチと空間的に相関のあるパッチに対して、相互情報量の最大化を行います。つまり、以下のように定式化できます。
max I(Φu(x), Φu+t(x))
ここで、uはピクセルuを中心としたパッチを示しており、そこからtだけ離れた場所のパッチとの相互情報量の最大化を行います。さらに、画像分類タスクと同じように、幾何学および色彩の変換をもとのパッチに対して行います。これを定式化したものが以下の式です。
max I(Φu(x), [g-1Φ(gx)]u+t)
なぜこの式になるのかは、変換gを左右反転の変換としてみると、想像しやすいと思います。あるxに対して$gx$と変換した後に、tだけずらすと、元の位置から反転した位置に対してtだけずらすことになります。そこで、g-1によってもとの位置に戻す処理が必要となります。
さらに、本論文ではoverclusteringという手法も使用しています。これは本来のクラス数よりも多くクラスタを用意するという(最終層のFC層の数を増やす)手法です。これを用いることによって、ノイズが含まれたデータを使用しても、良い特徴が得られるようになります。
実験
ここからはIICを用いた、画像分類タスクとセグメンテーションタスクに関する実験を紹介します。
使用データセット
・STL-10
ImageNetを教師なし学習用に適応したデータセットです。10クラス分類で各クラスに13Kの教師ありデータと、ラベルなしのデータが100K含まれています。
・CIFAR
低解像度の画像から構成されるデータセットで、今回の実験では、10・20・100クラスのCIFARデータセットを使用しています。
・MNIST
10クラスの手書き文字から構成されるデータセットです。
・COCO-Stuff
建物や水といった様々なクラスで構成されたセグメンテーション用のデータセットです。今回は、15クラスを選定して使用しています。なお、COCO-stuff-3は15クラスのうち、さらに3クラスを選定したデータセットです。
・Potsdam
道や車といった6クラスで構成された衛星画像のデータセットです。Potsdam-3は6クラスを3クラスに統合したデータセットです。
実験結果
・画像分類タスク
使用するモデルはResNet・Vgg11を使用しており、最終層のFC層の出力数は各データセットのクラス数と同じに設定しています。なお、実験では重みの初期化を5回行い、最も性能の良かったものと平均のスコアを表示しています。
実験は教師なし学習の枠組みと半教師あり学習の枠組みの二つで行っています。
教師なし学習の枠組みの実験では、画像を入力して、出力確率を得て(どの出力がどのクラスかはこの段階では分からない)、その後、出力クラスタがどのクラスにあたるのか、アサインメントしています。このアサインメントにはラベルを用いていますが、ネットワークのパラメータには影響しません。以下の図が実験の結果を表したものです。
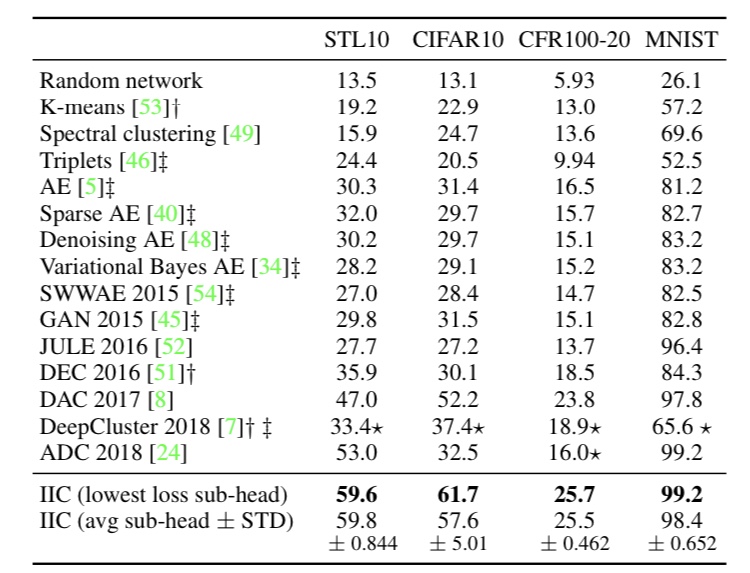
図3. 画像分類タスクにおける教師なし学習の結果
図3によると、IICは平均的に他の手法を圧倒する性能を出していることが分かります。これはIICが本質的に良い特徴を抽出できていることを表しています。これは以下の図を見るとより分かります。

図5. IICによる画像分類の例
図5の緑のバーは正解ラベルを、赤いバーは不正解である確率を示しています。IICは画像の背景などは無視をして、意味のある部分だけを抽出して出力を行うので、背景やノイズなどに惑わされて、他のクラスであるという予測を出力しないことが分かります。
半教師あり学習の枠組みの実験では、教師なしで学習したネットワークにランダムに初期化された分類層を付け加えて、教師データの一部を使用してチューニングを行います。この結果を示したのが、以下の図です。
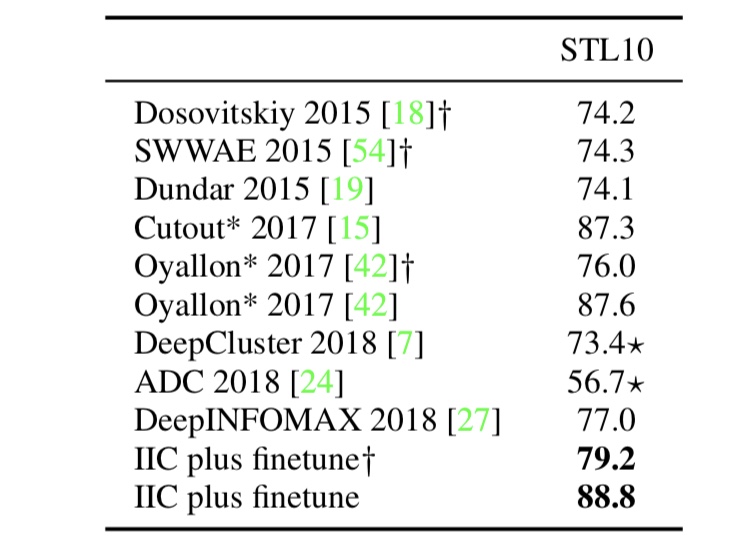
図4. 画像分類タスクにおける半教師あり学習の結果
図4中の✳︎は教師あり学習での結果を示しており、IICを用いた半教師あり学習は、教師あり学習の精度を上回っていることが分かります。これは先ほども述べたように、IICによる教師なし学習で、良い特徴が得られていることに起因するものです。
・セグメンテーションタスク
セグメンテーションタスクは、画像のパッチ毎にIICで学習したモデルを適応して、実験を行っています。以下の図が教師なし学習での実験結果です。
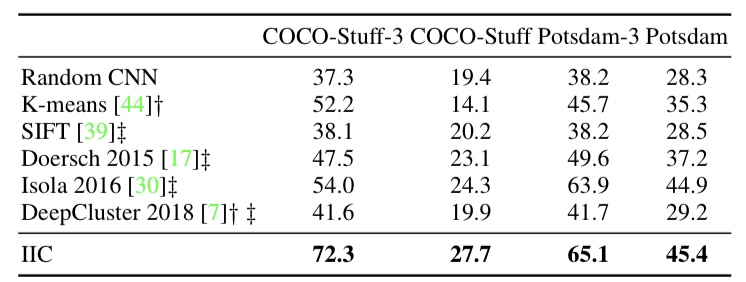
図6. セグメンテーションタスクにおけるIICの実験結果
セグメンテーションタスクでも、画像分類と同じようにアサインメントを行なっているため、定量的な評価ができています。なお、評価はピクセル毎の精度です。
図6から、IICによるセグメンテーションは他の手法より優れたものであることが分かります。以下の図はセグメンテーション結果の例です。

図7. セグメンテーションタスクにおけるIICの適応例
図7を見て分かるように、IICによるセグメンテーションは正解にほぼ一致していることが分かります。なお、✳︎は半教師あり学習での結果を表しています。
まとめ
本記事では、相互情報量を最大化する枠組みでニューラルネットワークを教師なしで学習する手法IICを紹介しました。IICは、従来の教師なし学習が抱えていた「クラスタが一つにまとまってしまう問題」および「ノイズに弱いという問題」を解決しています。
さらにIICはシンプルな手法でありながら、画像分類タスクおよびセグメンテーションタスクでSOTAを出しています。本論文では、画像認識タスクにIICを利用していますが、あるデータ$x$に対してペアを生成し、相互情報量が計算できれば、画像に限らず様々なデータに適応できる汎用性の高い手法です。
また、半教師あり学習にもすぐに適応できるという点において、実応用へ期待できる手法となっています。ラベル情報が大量に必要である深層学習手法が世の中を席巻する中、低いコストで精度が担保できる手法が今後、ますます注目されると個人的には考えています。読者の皆さまも、教師なし学習や半教師あり学習の研究動向に目を光らせてみてはいかがでしょうか。
この記事に関するカテゴリー








