Timeline Transformers Review

3 main points
✔️ Comprehensive review of Transformers for time-series data that have started to be published in recent years
✔️ Categorized in terms of both network structure and applications (prediction, anomaly detection, classification), Transformer's strengths and limitations are reviewed.
✔️ Future developments include explanations of pre-learning, GNNs, and NAS combinations.

Transformers in Time Series: A Survey
written by Qingsong Wen, Tian Zhou, Chaoli Zhang, Weiqi Chen, Ziqing Ma, Junchi Yan, Liang Sun
(Submitted on 15 Feb 2022 (v1), last revised 7 Mar 2022 (this version, v3))
Comments: Published on arxiv.
Subjects: Machine Learning (cs.LG); Artificial Intelligence (cs.AI); Signal Processing (eess.SP); Machine Learning (stat.ML)

code：  

The images used in this article are from the paper, the introductory slides, or were created based on them.

background

Since Transformer was published in 2017, it has been applied to many areas including NLP, CV, and conversation processing. Numerous paper reviews have also been published recently. ( ^{NLP1, 2}, ^{CV3, 4, 5}, Efficient Transformer, Attention ^Model6,7)

The transformer is also attractive for time series data modeling because it has demonstrated the ability to model long-term range dependence and interactions in series data. We have transformed Transformer to address the challenges specific to time series data. One of the main challenges is to capture long and short-term dependencies as well as seasonality and periodicity. Although Transformer has been mentioned in some of the time-series deep learning reviews so far, we have yet to see a comprehensive review on Transformer.

In this paper we summarize the main developments of the Time Series Transformer." After a short introduction to the "vanilla" Transformer, we present the classification from network modifications and applications. For the network, we will touch on both the low and high levels. For the applications, we will analyze the common time-series tasks: prediction, anomaly detection, and classification. For each, we analyze the strengths and limitations of Transformer. As a practical guide, we have conducted extensive experimental work investigating many aspects of time series modeling. These include robustness analysis, model size analysis, and seasonal trend decomposition analysis. Finally, we discuss potential future extensions.

Transformer Review

It has a "vanilla" Transformer encoder-decoder structure and is the most competitive neural sequence model. Each encoder and decoder has several identical blocks. Each encoder block consists of a multi-head self-attention module and a position-by-position forward propagation module. The decoder, on the other hand, consists of a multi-head self-attention and a position-by-position forward propagation module. The decoder, on the other hand, contains a cross-attention model that incorporates the inputs from the encoder between the multi-head self-attention and the position-by-position forward propagation modules.

Input encoding and positional encoding

Unlike LSTMs and RNNs, Transformer does not have recurrence or convolution. Instead, it uses positional encodings added to the input embedding to model sequence information. Some positional encodings are summarized below.

Absolute positional encoding

In the vanilla Transformer, for each position index t, the encoding vector is given by

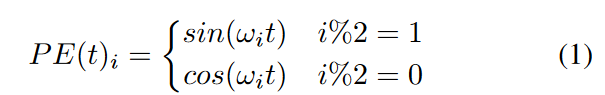
where ωi is your hand-made frequency for each dimension is the frequency of the first position embedding. Another way is to learn a more flexible set of positional embeddings for each position.

Relative Position Encoding

Following the intuition that positional relationships in pairs between input elements are more informative than element positions, relative position encoding methods have been proposed. For example, one such method is to add a learnable relative position embedding to the key of the attention mechanism. Besides absolute and relative position encoding, another method is to use hybrid position encoding, which combines them. Typically, the position encoding is added to the token embedding and sent to the Transformer.

Multihead Attention

In the Query-Key-Value (QKV) model, the scaled attentions of the inner product used by the Transformer are given by

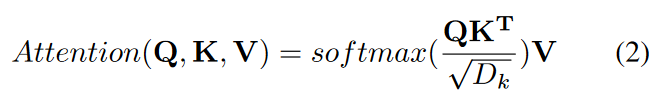
where query Q ∈ ^_RN×Dk, key K ∈ ^_RM×Dk, value V ∈ ^{_{RM×Dv and}} N, M denote the length of the query, and key (or value), and _Dk,Dv denotes the dimension of the key (or query) and value. Instead of a single attentional function, Transformer uses the learned projection. It is a simple and efficient way to learn a set of H different sets of multi-head attentions.

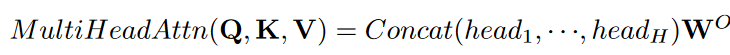
Forward propagation and residual networks

The feed-forward network for each location is

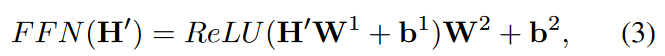
is a fully connected module, as in where H' is the output of the previous layer and^{W1∈_RDm×Df, W2∈_RDf×Dm,b1∈_RDf,b2∈_RDm} are learnable parameters. For deeper modules, a residual connection module and subsequent layer normalization modules are inserted around each module. In other words, 

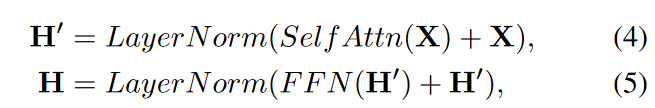
where Self Attn(.) denotes a self-attention module, and LayerNorm(.) indicates a layer normalization operation.

Classification of Time Series Transformers

To organize the existing time series transformers, we have prepared a classification in terms of network modification and applications, as shown in Fig. 1. According to this classification, we systematically review time-series Transformers. Based on the taxonomy, we systematically review the existing time-series Transformers. From a network change perspective, we summarize the changes made at both the module and architecture level of the Transformer to address the particular challenges of time series modeling. From an application perspective, classify the Time Series Transformer based on application tasks such as prediction, anomaly detection, classification, and clustering.

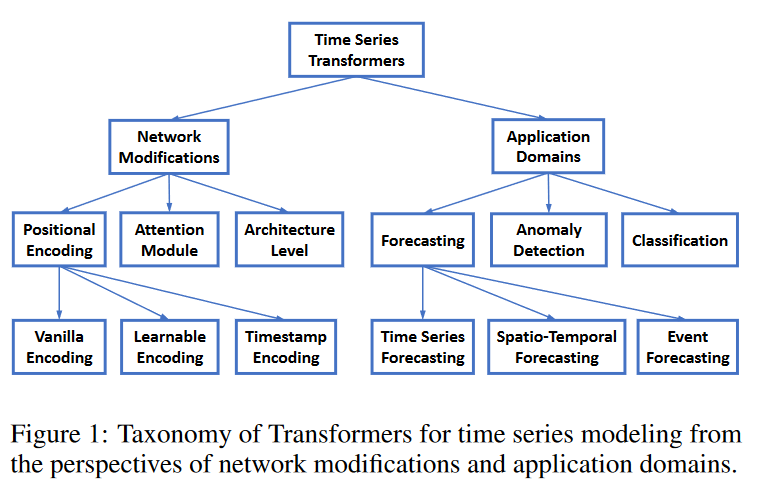
Network modification for time series

Since the position encoding Transformer is equivalent to permutation and the order of the time series is important, it is very important to encoding the positions of the input time series into the Transformer. A common design is to first encode the positions as vectors and then inject them into the model as additional input along with the input time series. How these vectors are obtained when using the Transformer to model the time series can be classified into three main categories.

Position encoder

Vanilla position encoding

Some work simply introduces vanilla position encoding, which is subsequently added to the input time series embedding and fed into the Transformer. While this simple application can extract some positional information from the time series, it fails to fully exploit the important features of time series data.

Learning position encoding

Since vanilla position encodings are handcrafted and are less expressive and adaptive, several studies have found that learning appropriate position embeddings from time-series data is much more effective. Compared to fixed vanilla position encodings, learned embeddings are more flexible and can be adapted to specific tasks. Zerveas et al. introduce an embedding layer in Transformer, which learns an embedding vector for each position index along with other model parameters. Lim et al. encoded the position embeddings using LSTM networks with the aim of better exploiting the sequential ordering information of the time series.

timestamp encoding

When modeling time series in a real-world scenario, you typically have access to timestamp information such as calendar timestamps (seconds, minutes, hours, weeks, months, years, etc.) or special timestamps (holidays, events, etc.). These timestamps are very useful in real applications, but are rarely utilized in vanilla Transformer. To alleviate this problem, Informer proposed to encode timestamps as an additional positional encoding using a learnable embedding layer. Similar timestamp encoding schemes were used in Autoformer and FEDformer.

Attention Module

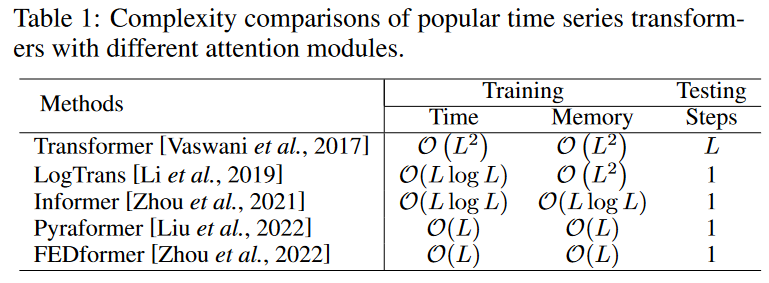
The heart of the Transformer is the self-attaching module. It can be viewed as a fully connected layer with weights that are dynamically generated based on similarity in pairs of input patterns. As a result, it shares the same maximum path length as a fully connected layer, but has far fewer parameters, making it suitable for modeling long-term dependencies. The time and memory complexity of the vanilla Transformer self-attachment module is O( ^L2), where L is the length of the input time series and is a computational bottleneck when processing long sequences To reduce the second-order complexity, many efficient transformers have been proposed, and can be classified into two main categories They can be classified into two main categories. (1) explicitly introducing sparsity bias in the attention mechanism, such as LogTrans and Pyraformer; (2) introducing sparsity bias in the attention mechanism, such as Informer and FEDformer; (3) introducing sparsity bias in the attention mechanism, such as Informer and FEDformer (2) introducing sparsity bias in the attentional mechanism, as in Informer and FEDformer. search for low-rank properties of the self-attention matrix to speed up the computation. Table 1 summarizes both the time and memory complexity of common Transformers applied to time series modeling.

Architecture-level innovation

In addition to addressing the individual modules of Transformers for modeling time series, some works are trying to revamp Transformers at the architectural level. Recent work has introduced a hierarchical architecture to the Transformer to take into account the multiple resolution aspect of time series. Informer inserts a maximum pooling layer of stride 2 between the attention blocks. This downsamples the series into half slices. Pyraformer designs a C-ary tree-based attention mechanism. In this mechanism, the nodes with the finest scale correspond to the original time series, while the nodes with coarser scales represent lower resolution series. Pyraformer has developed both intra- and inter-scale attachments to better capture temporal dependencies across different resolutions. In addition to the ability to integrate information across various multi-resolutions, the hierarchical architecture also has the advantage of efficient computation, especially for long time series.

Application of Time Series Transformer

prediction

Time Series Forecast

Prediction is the most common and important application of time series. LogTrans proposed convolutional self-attention by using causal convolution to generate queries and keys in the self-attention layer. This introduces a sparse bias (Logsparse mask) to the self-attention model, reducing the computational complexity from O( ^{L2) to} O(L log L). Instead of introducing sparsity bias explicitly, Informer selects O(log L) key queries based on query and key similarity and achieves similar improvements in computational complexity as LogTrans. We also design a generative style decoder that directly generates long-term forecasts and when using a single forward step forecast for the long-term forecast. avoid cumulative errors when using a single forward step forecast for the long-run forecast.

AST uses a generative adversarial encoder-decoder framework to train sparse Transformer models for time series prediction. It shows that adversarial training can improve time series prediction by directly shaping the output distribution of the network and avoiding the accumulation of errors due to one-step-ahead inference.

Autoformer devises a simple seasonal trend decomposition architecture with an autocorrelation mechanism that acts as an attention module. The autocorrelation block is not a conventional attention block. It measures the time-delay similarity between input signals and aggregates the top k similar subseries to produce an output with reduced complexity of O(L log L).

FEDformer uses Fourier and wavelet transforms to apply attentional operations in the frequency domain. It achieves linear complexity by randomly selecting a fixed-size subset of frequencies. It is worth noting that with the success of Autoformer and FEDformer, exploring self-attention mechanisms in the frequency domain of time series modeling has gained more attention in the community.

TFT designs multi-horizon prediction models with static covariate encoders, gating feature selection, and temporal self-attention decoders. It encodes and selects useful information from various covariates and performs prediction. It also maintains interpretability by incorporating global temporal dependencies and events.

SSDNet and ProTran combine the Transformer with a state-space model to provide probabilistic forecasts. SSDNet first uses Transformer to learn temporal patterns and estimate SSM parameters, then applies SSM to perform seasonal trend decomposition and maintain interpretable capabilities. ProTran designs a generative modeling and inference procedure based on variational inference.

Pyraformer designs hierarchical pyramidal attention modules with path-following binary trees to capture a range of time dependencies in linear time and memory complexity.

Aliformer performs sequential prediction on time-series data by using knowledge-based attention together with branching to modify and denoise the attention map.

Spatio-temporal prediction

In Spatio-temporal prediction, both temporal and spatio-temporal dependencies need to be considered for accurate prediction. Traffic Transformer designs an encoder-decoder structure using a self-attention module to capture temporal-temporal dependencies and a graph neural network module to capture spatial dependencies. The Spatio-Temporal Transformer for traffic flow prediction goes one step further. Not only do we introduce a temporal Transformer block to capture temporal dependencies, we also design a spatial Transformer block along with a graph convolutional network to better capture spatial-spatial dependencies. The spatio-temporal Graph Transformer designs an attention-based graph convolution mechanism that can learn complex spatio-temporal attention patterns to improve pedestrian trajectory prediction.

Event Forecasting

Event sequence data with irregular and asynchronous timestamps are naturally observed in many real-world applications. This is in contrast to normal time series data with equal sampling intervals. Event prediction or forecasting aims at predicting the time and mark of future events considering the history of past events and is often modeled by a Temporal Pojnt Process ( TPP ). Recently, some neural TPP models have begun to incorporate Transformer to improve their event prediction performance. The Self-attentive Hawkes process ( SAHP ) and the Transformer Hawkes process ( THP) employ the Transformer encoder architecture to summarize the impact of historical events and compute an intensity function for event prediction. They modify the position encoding by converting the time interval to a sine function so that intervals between events are available. Subsequently, a more flexible named Attentive Neural Datalog ( A-NDTT) is proposed, which extends the SAHP/THP scheme by carefully embedding all possible events and times. Experiments show that it better captures advanced event dependencies than existing methods.

detecting abnormal conditions

Deep learning also triggers new developments for anomaly detection. Since deep learning is a kind of representation learning, reconstruction models play an important role in the anomaly detection task. Reconstruction models aim at learning a neural network that maps a vector from a simple predefined source distribution Q to an actual input distribution ^P+. Q is usually Gaussian or uniformly distributed. The anomaly score is defined by the reconstruction error. Intuitively, the higher the reconstruction error, the less likely it is to be due to the input distribution, resulting in a higher anomaly score. A threshold is set to distinguish between anomaly and normality. Recently, Meng et al. revealed the advantages of using Transformer for anomaly detection over other traditional models (such as LSTM) that are time dependent. In addition to higher detection quality (measured at F1), transformer-based anomaly detection is significantly more efficient than LSTM-based methods, mainly due to the parallel computation in the Transformer architecture. In several studies, including TranAD, MT-RVAE, and TransAnomaly, researchers have used Transformer proposed to combine Transformer with neural generative models such as VAE and GAN for better reconstruction models in anomaly detection. for better reconstruction models in anomaly detection.

TranAD proposes an adversarial training procedure to amplify reconstruction errors because simple Transformer-based networks tend to miss small deviations in anomalies. The GAN-style adversarial training procedure is designed with two Transformer encoders and two Transformer decoders to obtain stability. Isolation studies show that replacing the Transformer-based encoder-decoder reduces the performance of the F1 score by nearly 11% and the importance of the Transformer architecture for anomaly detection.

MT-RVAE and TransAnomaly both combine VAE and Transformer, but for different purposes. TransAnomaly combines VAE and Transformer to enable more parallelization and reduce the learning cost by about 80%. In MT-RVAE, the multi-scale Transformer is designed to extract and integrate time series information at different scales. This overcomes the shortcomings of traditional Transformers where only local information is extracted for sequential analysis. Several time series Transformers are designed for multivariate time series where the Transformer is combined with a graph-based learning architecture such as GTA. Note that MT-RVAE is also for multivariate time series, but with fewer dimensions or insufficient close relationships between sequences where graph neural network models do not perform well. To address these issues, MT-RVAE modifies the position encoding module and introduces a functional learning module. GTA includes a graph convolution structure to model the influence propagation process. Like MT-RVAE, GTA considers "global" information, but replaces vanilla multi-head attention with a multi-branch attention mechanism, a combination of global learning attention, vanilla multi-head attention, and neighborhood convolution.

AnomalyTrans combines Transformer and Gaussian Prior-Association to better identify rare anomalies. Although motivated by the same motivation as TranAD, AnomalyTrans achieves this goal in a very different way. It can be insightful that anomalies are difficult to establish a strong association with the series as a whole, but easier at adjacent time points compared to normal. In AnomalyTrans, pre-association and series association are modeled simultaneously. In addition to the loss of reconstruction, the anomaly model is optimized by a minimax strategy, which constrains prior and series associations for more discernible association discrepancies.

Classification.

Transformer has proven to be effective in a variety of time series classification tasks due to its excellent ability to capture long-term dependencies. Classification Transformers typically employ a simple encoder structure where the self-attention layer performs representation learning and the feedforward layer generates probabilities for each class.

GTN uses a two-tower Transformer, with each tower performing time-step-by-time-step attention and channel-by-channel attention, respectively. A learnable weighted concat (also called "gating") is used to integrate the functions of the two towers. The proposed extension of Transformer achieves SOTA results on 13 multivariate time series classifications. Rußwurm et al. studied a self-attention based Transformer for raw optical satellite time series classification and obtained the best results compared to RNN and CNN.

A pre-trained Transformer is also investigated in the classification task. Yuan et al. study Transformer for time series classification of raw optical satellite images. Due to limited labeled data, the authors use a self-supervised pre-training schema. Zerveas et al. introduce an unsupervised pre-training framework where models are pre-trained on proportionally masked data. The pre-trained models are fine-tuned in downstream tasks such as classification. Yang et al. propose the use of large-scale pre-trained speech processing models for downstream time series classification problems, generating 19 competing results on 30 well-known time series classification datasets.

experiment

Robustness Analysis

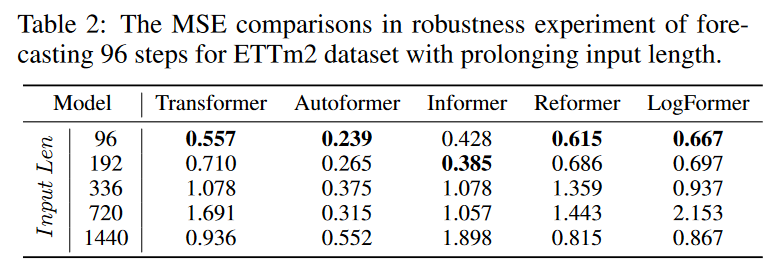
Many of the work described above carefully designs the attention module so as to reduce quadratic computation and memory complexity, but in practice uses short fixed-size inputs to achieve the best results in the reported experiments. The actual use of such an efficient design is questionable. We run robust experiments with extended input sequence lengths to test the predictive power and robustness of the design when processing long input sequences. As shown in Table 2, the various Transformer-based models degrade rapidly when the prediction results are compared to extending the input length. This phenomenon makes many carefully designed Transformers impractical for long-term prediction tasks because they cannot effectively exploit long input information. More work needs to be done to fully exploit long sequence input other than simply executing it.

model size analysis

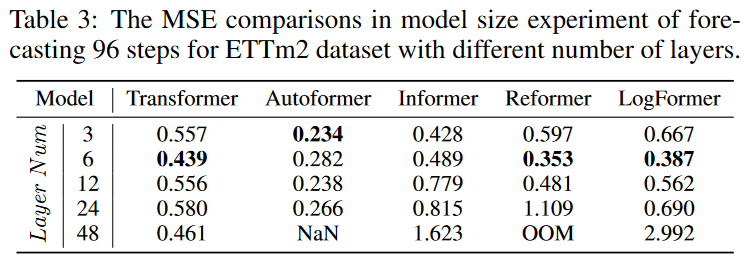
Prior to its introduction into the field of time series prediction, Transformer demonstrated outstanding performance in the NLP and CV communities. One of the key advantages that Transformer has in these areas is the ability to increase the predictive power by increasing the model size. Typically, model capacity is controlled by the Transformer layer number. The layer number is usually set between 12 and 128 in CV and NLP. However, as shown in the experiments in Table 3, when comparing the prediction results for different Transformer models with different layer numbers, the shallowest Transformer with 3 to 6 layers wins. The question arises as to how to design an appropriate Transformer architecture with deeper layers to increase the model capacity and achieve better prediction performance.

Seasonal trend decomposition analysis

In the latest work, researchers have started to realize that seasonal trend decomposition is an important part of Transformer's performance in time series forecasting. As a simple experiment shown in Table 4, we test different attention modules using the moving average trend decomposition architecture proposed by Wu et al. The seasonal trend decomposition model can significantly improve the performance of the model by 50% to 80%. This is a unique block, and such performance gains due to decomposition seem to be a consistent phenomenon in time series forecasting in the Transformer application and are worth further investigation.

Opportunities for further research

induced bias

Vanilla Transformer assumes nothing about the patterns and properties of the data. It is a general and universal network for modeling long-range dependencies, but it comes at a cost. This means that training Transformer to avoid overfitting the data requires large amounts of data. One important feature of time series data is its seasonal/periodic and trend patterns. Several recent studies have shown that incorporating serial periodicity or frequency processing into the Time Series Transformer can significantly improve its performance. Thus, one future direction is to investigate more effective ways to induce induced bias in the Transformer based on an understanding of time series data and specific task characteristics.

Transformer and GNN

Multivariate and spatio-temporal time series are becoming increasingly common in applications, requiring additional methods to handle high dimensions, especially the ability to capture fundamental relationships between dimensions. The introduction of graph neural networks (GNNs) is a natural way to model spatial dependencies or relationships between dimensions. Recently, several studies have shown that the combination of GNNs and Transformer/Attention can be used for traffic forecasting and multimodal forecasting but can also provide a better understanding of spatio-temporal dynamics and potential causal relationships. The combination of Transformer and GNN is an important future direction for effective spatio-temporal modeling in time series.

Pre-Learning Transformer

Large pre-trained Transformer models allow NLP and CV performance on a variety of NLP and CV tasks has been significantly improved. However, work on pre-trained Transformers for time series is limited, and existing work has mainly focused on time series classification. Therefore, it is left to future research on how to develop suitable pre-trained Transformer models for different time series tasks.

Transformer with NAS

Hyperparameters such as embedding dimension, number of heads, number of layers, etc. can have a significant impact on Transformer performance. Manually setting these hyperparameters is time consuming and often results in suboptimal performance. Neural Architecture Search (NAS) is a popular technique for discovering effective deep neural architectures, and the use of NAS in NLP and CV to automate Transformer design can be found in recent work. For industry-scale time series data, which can be both high-dimensional and long-length, automatically discovering Transformer architectures that are both memory and computationally efficient is of practical importance and an important future direction for time series Transformers.

summary

This paper provides a comprehensive survey on Time Series Transformers in different tasks. The reviewed methods are summarized in a new taxonomy consisting of network modifications and application domains. Representative methods in each category are summarized, their strengths and weaknesses are discussed through experimental evaluation, and directions for future research are highlighted.

• 
• 
• 

Categories related to this article

• Transformer
• Time Series
• Survey, Review
• Time-series