Unsupervised Learning Method IIC By Maximizing The Amount Of Mutual Information Is Now Available! Has It Surpassed The Accuracy Of Supervised Learning?

Article 01/02/2020

3 main points

✔️An unsupervised learning method, IIC, was proposed to learn neural networks in a framework that maximizes the amount of mutual information.
✔️No clustering is required as it is possible to train a neural network that outputs predictions as they are.
✔️It solves the problem of clusters being grouped together and susceptibility to noise in traditional unsupervised learning methods.

Invariant Information Clustering for Unsupervised Image Classification and Segmentation
Written by Xu Ji, João F. Henriques, Andrea Vedaldi
(Submitted on 22 Aug 2019)
subjects : Computer Vision and Pattern Recognition (cs.CV); Machine Learning (cs.LG)
Paper Official Code COMM Code

Introduction

In recent years, deep learning methods have begun to be used in a variety of situations. This is because deep learning methods perform very well. However, training deep learning models requires a large amount of labeled data, which limits the real-world applications of deep learning methods.
With this background, unsupervised learning, which does not require label information, is gaining attention. In unsupervised learning, the goal is to get good features from the data. For example, if we want to classify the data, we can say that data belonging to the same class are grouped together and samples belonging to different classes are separated, which is a good feature.
However, traditional unsupervised learning has two major problems. The first problem is that the clusters are often grouped together or disappear when clustering is performed based on the features. The second problem is that we cannot get good features if the training data contains noisy data.
To solve the problems mentioned above, we propose a method of learning the network by maximizing the mutual information (IIC). We will briefly introduce the mutual information content in a later section, but it enables us to solve the two problems. The following figure shows a visualization of the results of the image classification and segmentation by IIC.

Figure 1. Image classification and visualization of segmentation results using IIC

In this paper, we use IIC to experiment with an image classification task and a segmentation task, and we produce SOTA for both tasks. We also show that when IIC is adapted to semi-supervised learning, it exceeds the accuracy of supervised learning.
Another advantage of IIC is that it is a general-purpose method and can be used for a variety of tasks if the mutual information content of the data can be calculated.

Benefits of Maximizing Mutual Information

In this section, we briefly introduce mutual information content and explain the learning benefits of maximizing mutual information content.
First, the mutual information content is defined for a pair of probability distributions (z, z') as follows. In this paper, (z, z') represents a probability distribution where (z, z') is the output of the neural net $Φ$ with respect to the input (x, x'). That is, $z = Φ(x)$.

$I(z,z') = H(z) - H(z | z')$

where $H(z)$ is the entropy with respect to z and $H(z | z')$ is the conditional entropy at the source given by z'. Entropy is a measure of information ambiguity; the more ambiguous the information, the greater the value. (It is maximum in a uniform distribution and 0 in a probability distribution that takes 1 at a certain point.)
In the IIC, we aim to maximize the mutual information content by learning neural nets Φ. This means to make the first item of mutual information larger and the second item smaller.
First, increasing the first item, $H(z)$, means that the learning proceeds in such a way that z approaches a uniform distribution, which eliminates the need for it to clump together into a single cluster. However, maximizing $H(z)$ alone will result in a uniform distribution of z, which is a meaningless output. Here, by decreasing the second item, $H(z|z')$, the learning proceeds to make the output somewhat more meaningful.

Figure 2. The learning process of IIC in MNIST data.

Figure 2 shows the learning process of the IIC in the MNIST dataset. The learning progresses from left to right. Initially, the features are grouped together, but as the training progresses, it can be seen that they are separated from the other classes.
Also, if z and z' are similar, the conditional entropy of the second term will be smaller. This is because if we give z' similar to z, the ambiguity is reduced. In other words, the network will be trained to output predictions by focusing on the common parts of x and x'. In this way, the network is trained so that samples belonging to the same class have the same output.

Proposal methodology

Now that we have seen the benefits of mutual information maximization, let's discuss the proposed method, IIC, which consists of the following two major steps.

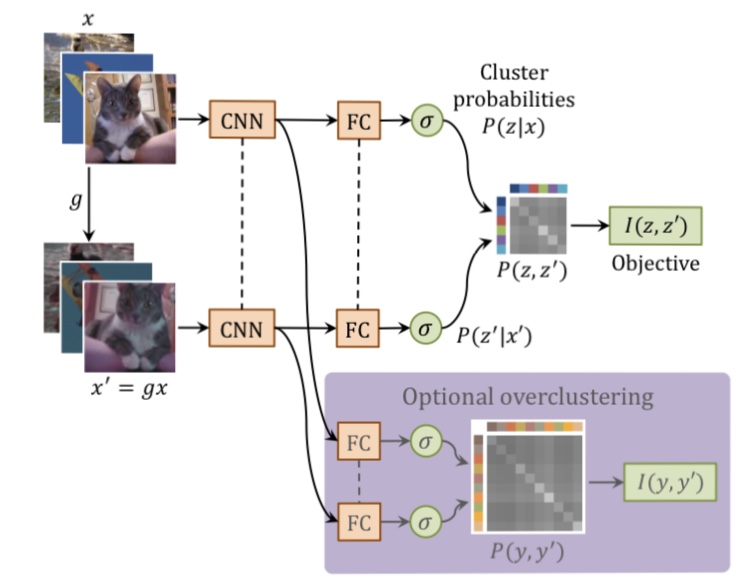
Figure 3: Overview of the IIC

(1) Generate a pair of $x$ data $x'$ based on $x$.
(2) Train the network to maximize $I(z, z')$ by inputting $(x, x')$ into the neural net $Φ$ and getting the output $(z, z')$.
In this paper, we adapt IIC to the task of image classification and the task of segmentation. For each task, let's look at steps (1) and (2).

Image classification tasks

When performing the image classification task, we generate x', a pair of x's, by geometrically deforming or changing the contrast of the x's in order to generate x'. In other words, a transformation g is defined and x' is represented by the following formula. $x' = gx$
By learning to maximize the amount of mutual information with those that have altered themselves in this way, we can focus on only the parts of the data that are meaningful, even with the added noise.

Segmentation task

The segmentation task requires a pixel-by-pixel classification. Then, a pixel and its neighbors are spatially correlated with each other.
Therefore, the IIC divides the image into patches and maximizes the mutual information content for patches that are spatially correlated with a certain patch. In other words, we can formulate it as follows.

max I( Φu (x), Φu+t (x))

Here, u indicates a patch centered on pixel u, from which we maximize the amount of mutual information with patches located only t away from it. In addition, as in the image classification task, geometric and color transformations are performed on the original patches. This is formulated in the following formula.

max I( Φu (x), [ g-1Φ (gx) ]u+t )

It's easy to imagine why this equation is the case if we consider the transformation g to be a left-right inversion. If you convert $gx$ to a certain x and then shift it by t, you will shift it by t in relation to the inverted position from the original position. Therefore, it is necessary to return to the original position by g-1.
Furthermore, we also use a technique called overclustering, which is a technique to prepare more clusters than the original number of classes (i.e., increase the number of FCs in the final layer). This is a technique to prepare more clusters than the original number of classes (i.e., to increase the number of FC layers in the final layer). By using this method, we can use noisy data and still get good features.

Experiment

In this section, we will introduce experiments on image classification and segmentation tasks using the IIC.

dataset used

STL-10
This dataset is an adaptation of ImageNet for unsupervised learning, containing 13K supervised data and 100K unlabeled data per class in 10 classes.

CIFAR
A dataset consisting of low-resolution images, and in this experiment, we used the 10, 20, and 100 class CIFAR datasets.

MNIST
This dataset consists of 10 classes of handwritten characters.

COCO-Stuff
This is a data set for segmentation consisting of various classes such as buildings and water. In this case, 15 classes are selected for use in this dataset. For COCO-stuff-3, 3 more classes are selected from the 15 classes.

Potsdam.
Potsdam-3 is a satellite image dataset consisting of 6 classes of roads and cars.

Experimental results

Image classification tasks
The model used is ResNet-Vgg11, and the number of outputs in the final FC layer is set equal to the number of classes in each dataset. Note that the weights were initialized five times in the experiment and the best performing and average scores are shown.
The experiment is conducted in two frameworks: an unsupervised learning framework and a semi-supervised learning framework.
In the unsupervised learning framework experiments, we input an image, get the output probability (we don't know which output is which class at this stage), and then assign which class the output cluster is in. We use labels for this assignment, but they do not affect the parameters of the network. The following figure shows the results of the experiment.

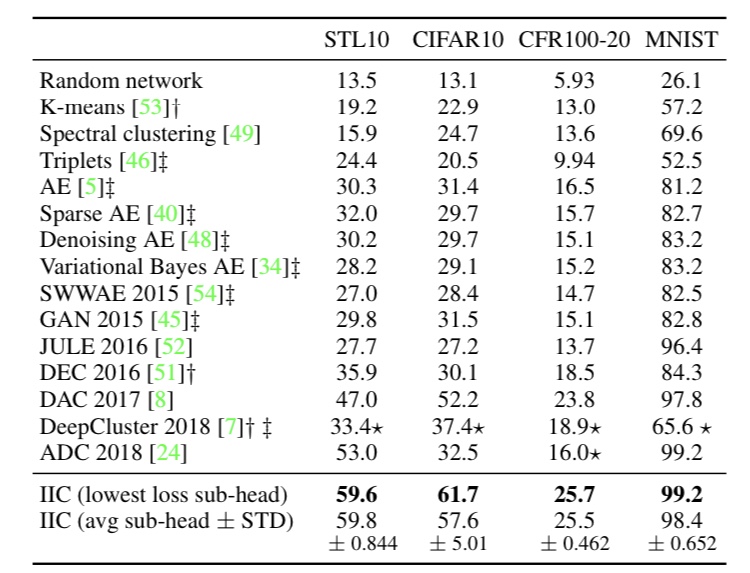
Figure 3. Results of unsupervised learning in an image classification task.

Figure 3 shows that IIC performs overwhelmingly better than other methods on average. This indicates that IIC is able to extract intrinsically good features. This can be seen more clearly in the following figure.

Figure 5: Example of image classification by IIC

The green bars in Figure 5 show the correct label and the red bars show the probability of being incorrect; you can see that the IIC ignores the background and other aspects of the image and extracts only the meaningful parts of the output, so it doesn't output predictions that it is another class because it is confused by the background and noise.
In the semi-supervised learning framework experiment, we add a randomly initialized taxonomic layer to the unsupervised network and tune it using some of the teacher data. The following figure shows the results of this process.

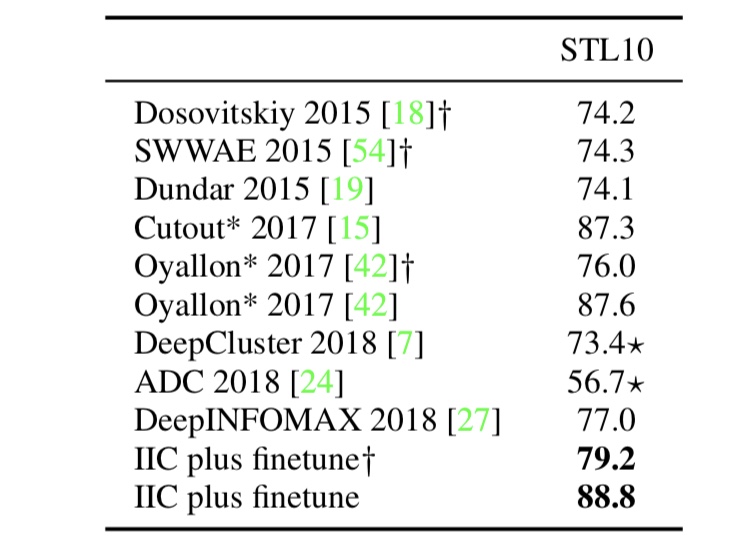
Figure 4. Results of semi-supervised learning in an image classification task.

The ✳︎ in Figure 4 shows the results for supervised learning, and we can see that semi-supervised learning with IIC exceeds the accuracy of supervised learning. This is due to the fact that unsupervised learning with IIC has good features, as we mentioned earlier.

Segmentation tasks

The segmentation task has been experimented with by adapting the model trained by IIC for each patch of images. The following figure shows the results of the experiment for unsupervised training.

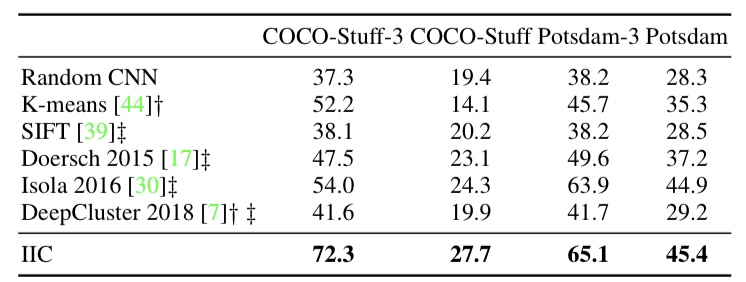
Figure 6. Experimental results of IIC in the segmentation task.

The segmentation task has the same assignment as the image classification, so it can be evaluated quantitatively. Note that the evaluation is on a per-pixel basis of accuracy.
Figure 6 shows that the segmentation by IIC is superior to other methods. The following figure shows an example of the segmentation results.

Figure 7. Examples of IIC adaptations in segmentation tasks.

As can be seen in Figure 7, we can see that the segmentation by IIC is roughly consistent with the correct answer. Note that ✳︎ represents the results for the semi-supervised learning.

Summary

In this article, we introduced IIC, a method for unsupervised learning of neural networks in a mutual information-maximizing framework, which solves the problem of clusters being grouped together and susceptibility to noise, which has been a problem of conventional unsupervised learning.
Furthermore, IIC is a simple method, yet it produces SOTA in the image classification task and segmentation task. In this paper, we use IIC for the image recognition task, and it is a highly versatile method that can be applied to a variety of data, not only images, as long as we can generate a pair of data $x$ and calculate the mutual information content.
In addition, it is a promising method for real-world applications in that it can be adapted to semi-supervised learning right away. As deep learning methods that require a large amount of label information dominate the world, I personally believe that low-cost, accurate methods that can guarantee accuracy will attract more and more attention in the future. I encourage readers to keep a close eye on research trends in unsupervised and semi-supervised learning.