
I-ViT: Compute ViT In Integer Type! ?Shiftmax And ShiftGELU, Which Evolved From I-BERT Technology, Are Also Available!
3 main points
✔️ Proposed I-ViT with all Vision Transformer calculations in integer type
✔️ Softmax and GELU with bit shift for further speedup
✔️ 3.72~4.11x speedup compared to no quantization
I-ViT: Integer-only Quantization for Efficient Vision Transformer Inference
written by Zhikai Li, Qingyi Gu
(Submitted on 4 Jul 2022 (v1), last revised 7 Aug 2023 (this version, v4))
Comments: ICCV 2023
Subjects: Computer Vision and Pattern Recognition (cs.CV)
code:
The images used in this article are from the paper, the introductory slides, or were created based on them.
Introduction
The Vision Transformer (ViT) is the model that has achieved the highest accuracy in various computer vision tasks.
However, the challenge is that the considerable storage and computational overhead makes it difficult to develop and efficiently reason at edge devices.
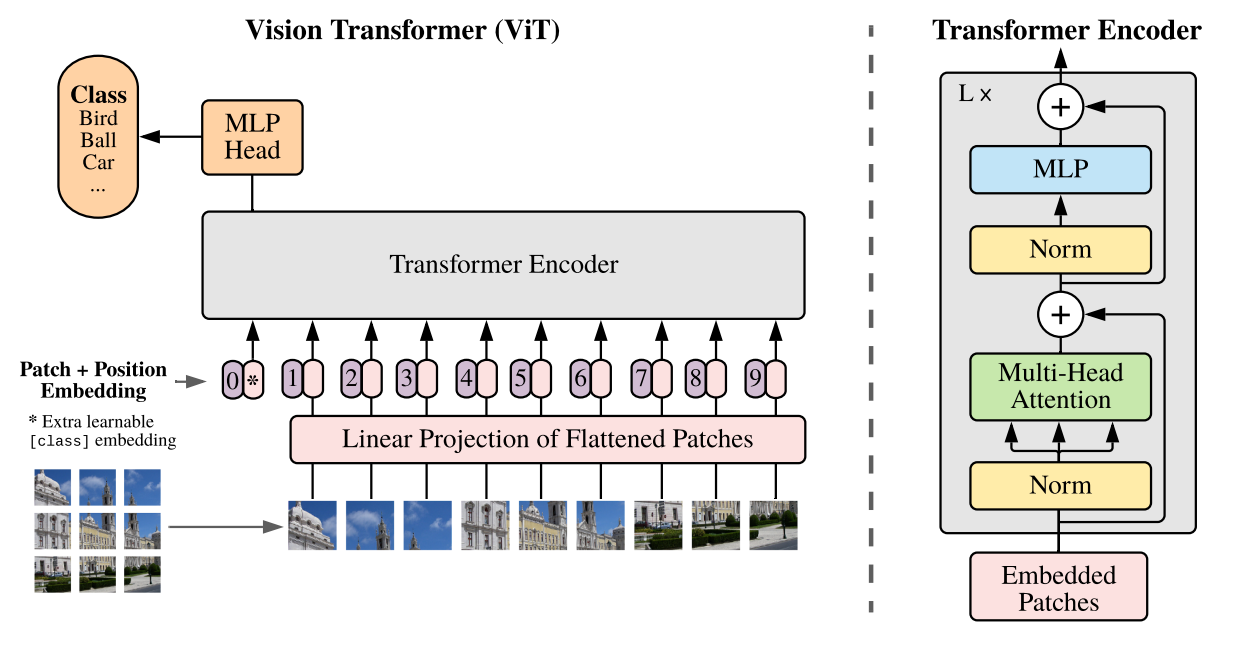
Vision Transformer [1].
Therefore, research on model quantization, which improves efficiency by reducing the representation accuracy of weights and activation parameters, is also underway in ViT.
FasterTransformer has succeeded in quantizing non-linear operations to integer types and has achieved an increase in inference speed. However, the nonlinear arithmetic part still leaves room for efficiency improvement, and there is a cost incurred in the exchange between integer and floating-point operations.
Therefore, this paper proposes I-ViT, whichallows all computations in ViT to be handled in integer form.
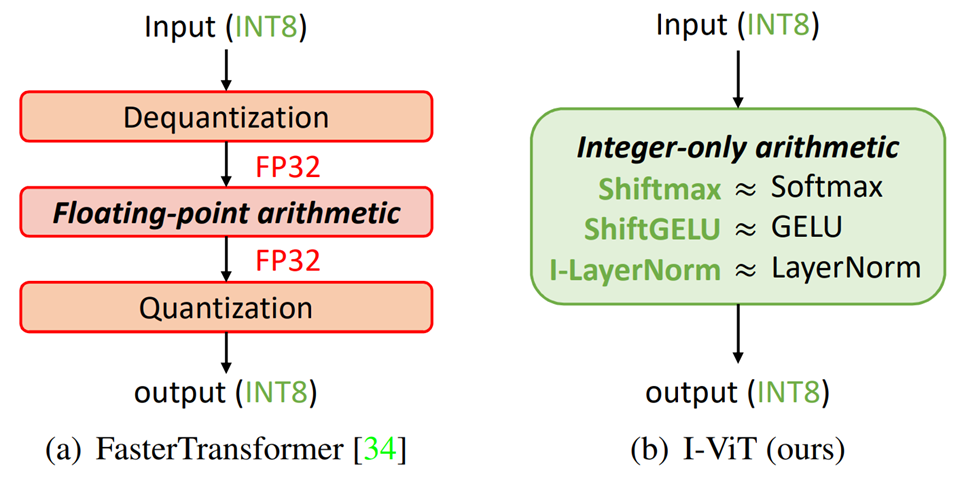
Proposed method: I-ViT
Big picture
The proposed method I-ViT is a ViT that can completely process only integer types.
The method of quantization from floating-point type to integer type is based on symmetric uniform quantization represented by the following equation.
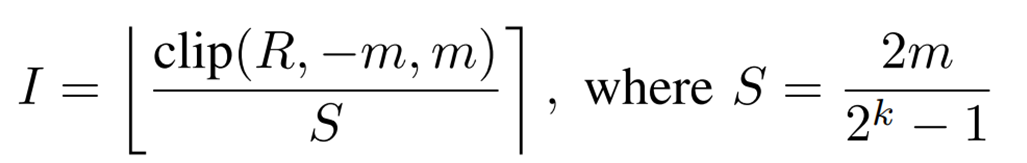
R is the floating point value, I is the quantized integer value, S is the scaling factor in quantization, m is the clipping value, k is the quantization bit precision, and [] is the round function.
The following figure shows the overall picture of the proposed method I-ViT. 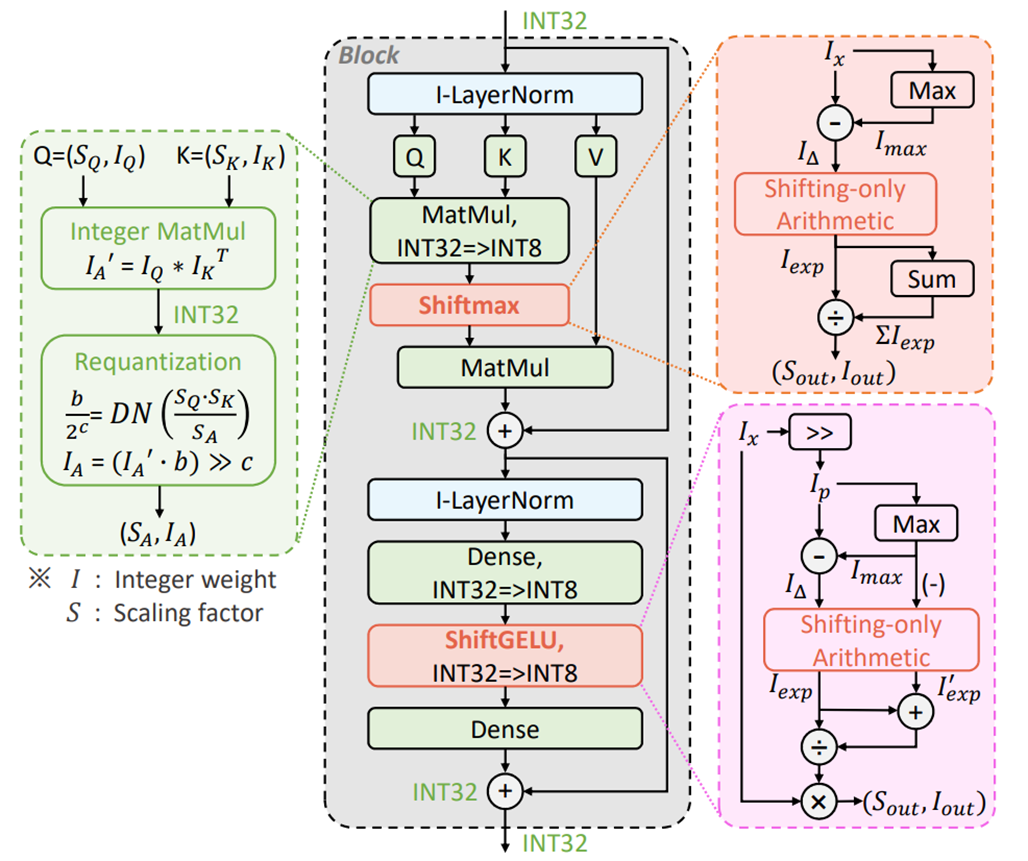
Linear operations such as inner product (MatMul) and all-combining layer (Dense) are performed by applying Dyadic Arithmetic to the integer type.
On the other hand, it cannot be applied directly to nonlinear operations such as Softmax, GELU, and LayerNorm.
Therefore, the proposed Shiftmax, ShiftGELU, and I-LayerNorm, respectively, enable operations on integer types.
I-LayerNorm is the same method employed in I-BERT introduced previously, while Shiftmax and ShiftGELU are more advanced versions of the methods used in I-BERT.
I-BERT has been introduced in AI-SCHOLAR before, so please check it out along with this article: I-BERT: BERT that can be inferred with integer types only
Dyadic Arithmetic for Linear
Dyadic arithmetic is a method to realize floating-point operations in scaling factor using integer bit shifts, which makes it possible to realize linear operations using only integer types.
Originally designed for CNN, but can also be used for linear operations in ViT. (convolution layer in embedding layer, inner product in transformer layer, all-combining layer)
In this section, we will take the inner product as an example to see how to calculate it.
![]() If
If ![]() , then the inner product
, then the inner product ![]() can be expressed as follows.
can be expressed as follows. ![]()
In this case, ![]() is of type int32, so it is converted to type int8.
is of type int32, so it is converted to type int8.
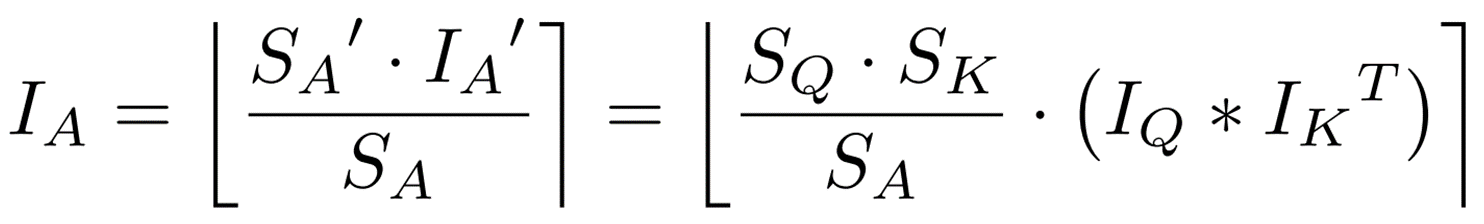
where ![]() is the pre-calculated scaling factor for output activity.
is the pre-calculated scaling factor for output activity.
Also, since ![]() is a float type, it is converted to a dyadic number (DN) using the following formula.
is a float type, it is converted to a dyadic number (DN) using the following formula. 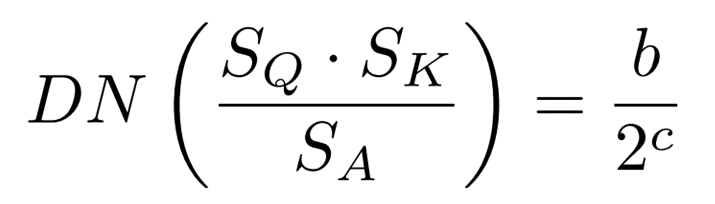 To summarize the operations up to this point, the inner product of type int only can be computed using bit shifting as follows
To summarize the operations up to this point, the inner product of type int only can be computed using bit shifting as follows 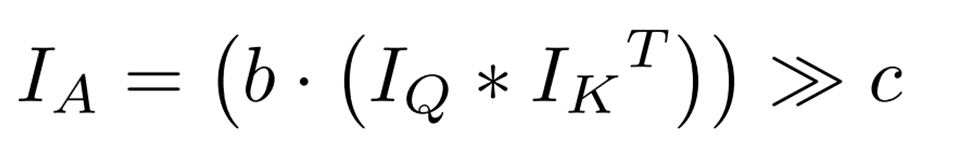
Integer-only Softmax: Shiftmax
In ViT, softmax is used to convert attention scores into probabilities.
Because Softmax is nonlinear, the dyadic arithmetic described above is not directly applicable. Therefore, Shiftmax is proposed in this paper.
First, Softmax is expressed in terms of scaling factor and quantized integer values as follows. 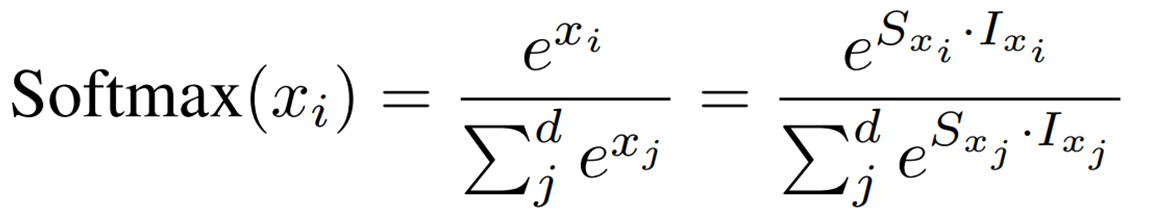
To smooth the data distribution and prevent overflow, restrict the range as follows 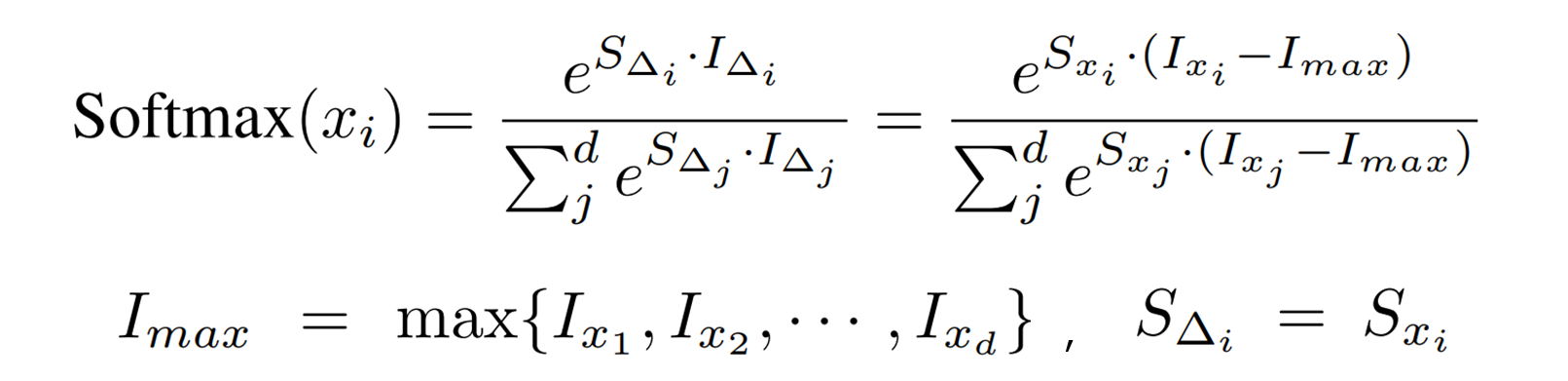
Next, to perform the calculation with bit shifts, we convert the base of the exponential function from e to 2 as follows 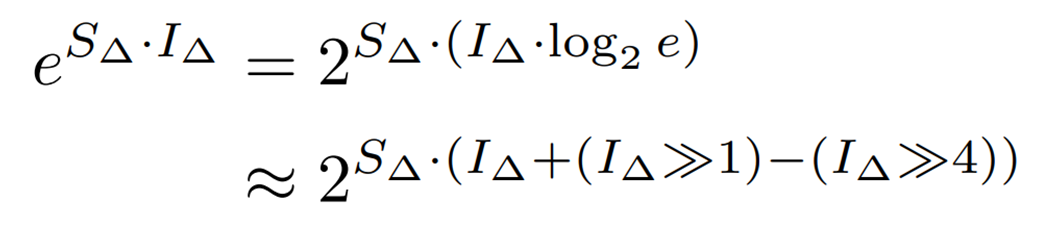 Here we use the following approximation
Here we use the following approximation
![]()
Furthermore, since ![]() is not an integer type, it is separated into
is not an integer type, it is separated into
integer part ( ![]() ) and decimal part (
) and decimal part ( ![]() ) as follows.
) as follows.
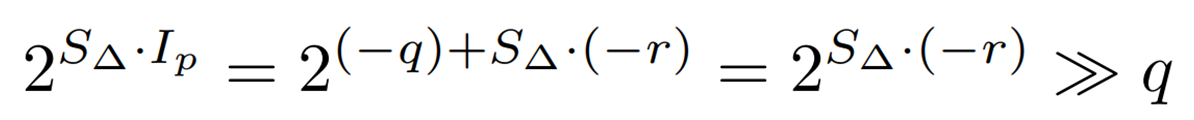
To reduce the computational complexity here, we approximate ![]() in the range of (-1, 0] by a linear function as follows
in the range of (-1, 0] by a linear function as follows
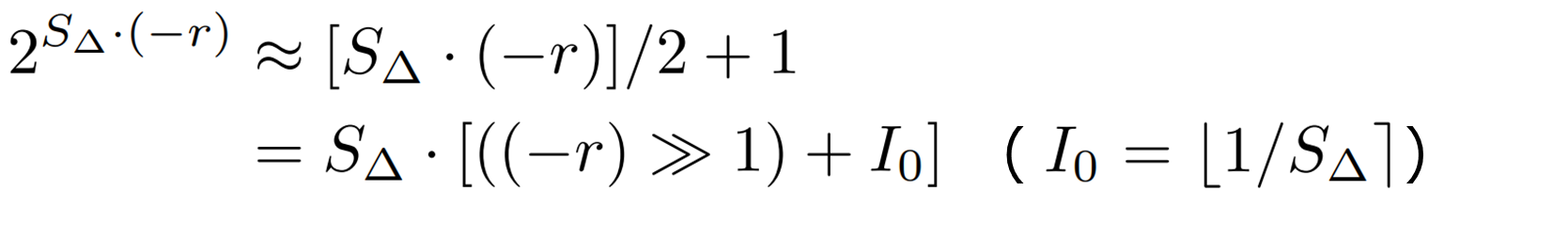
So far, the computation of the exponential function in Softmax can be expressed in the form of scaling factor and quantized integer type ( ![]() ) ( ShiftExp ).
) ( ShiftExp ).
Using ShiftExp, we obtain the final expression for Shiftmax, the integer-only operation of Softmax, as follows 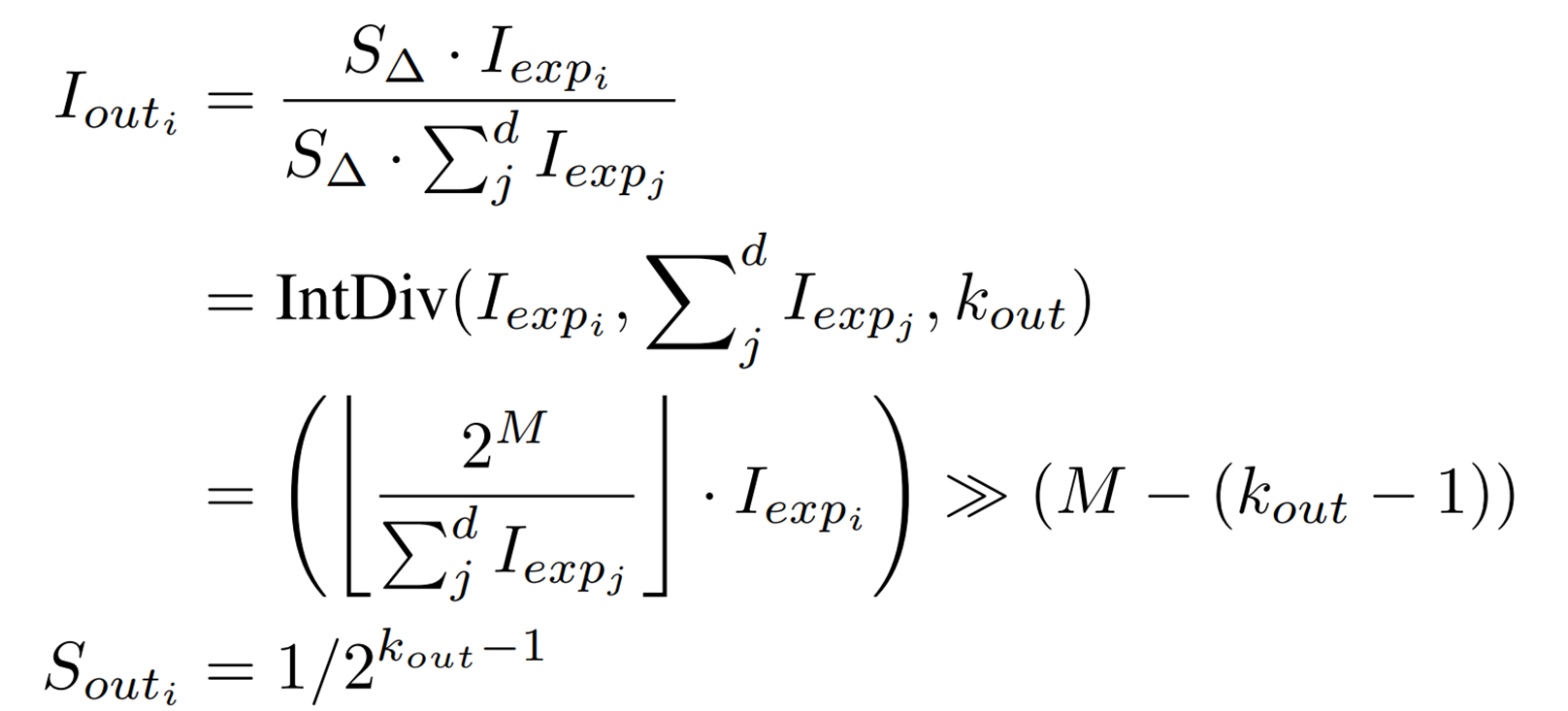
![]() is a function that performs division of type int, where
is a function that performs division of type int, where ![]() is the integer to be divided,
is the integer to be divided, ![]() is the integer to be divided, and
is the integer to be divided, and ![]() is the output bit width.
is the output bit width.
Finally, a summary of Shiftmax's algorithm is shown below.

Integer-only GELU: ShiftGELU
It is known that GELU is a nonlinear activation function in ViT and can be approximated using the sigmoid function ( ![]() ) as follows
) as follows 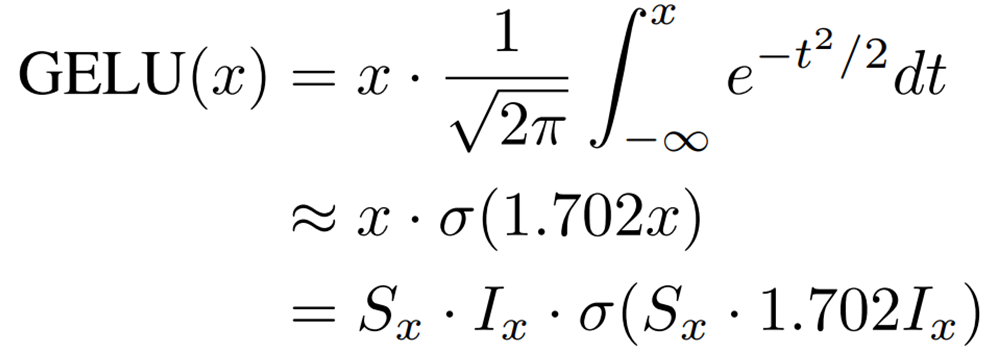
![]() So
So ![]() can be calculated using bit shifting as follows
can be calculated using bit shifting as follows
![]()
The sigmoid function can also be expressed as follows 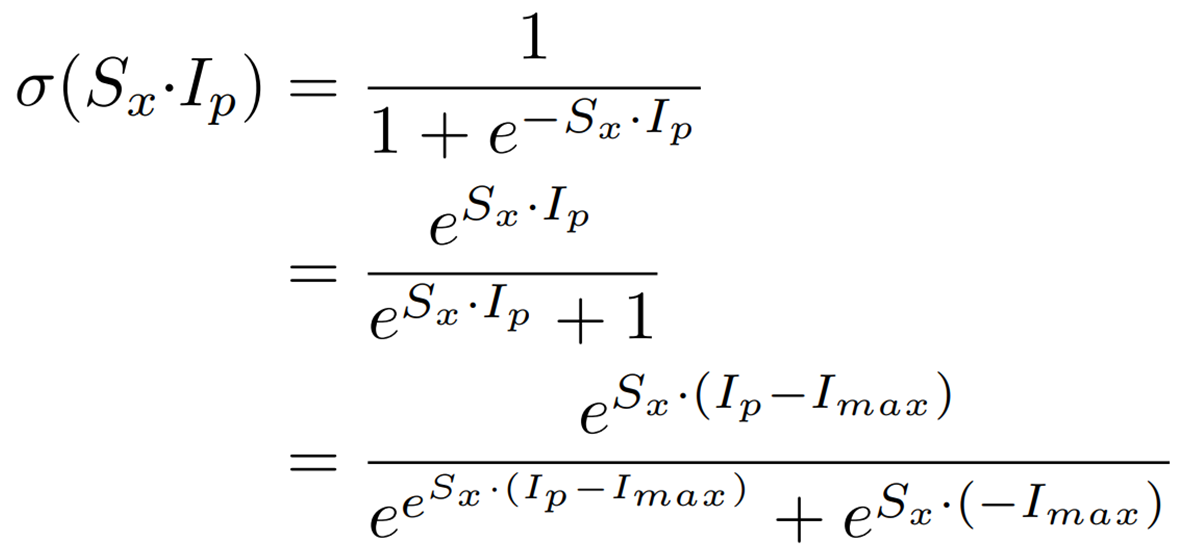
From this expression, it can be seen that the sigmoid function can be computed using only integer types by using ShiftExp and IntDiv as described in Shiftmax.
Finally, a summary of ShiftGELU's algorithm is shown below. 
I-LayerNorm
LayerNorm standardizes the hidden layer features as follows
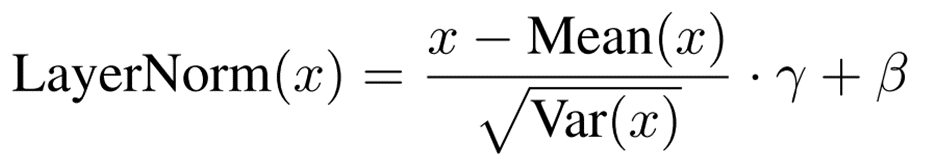
While BatchNorm uses the fixed values obtained by training in inference, LayerNorm requires the mean and standard deviation to be calculated in inference as well.
In integer arithmetic, the mean and variance of the data can be easily calculated, but the square root operation for the standard deviation cannot be performed.
For this reason, we propose an improved version of the light-weight integer iterative approach that uses bit shifting.
Repeat the following incremental formula up to 10 iterations until ![]() .
.
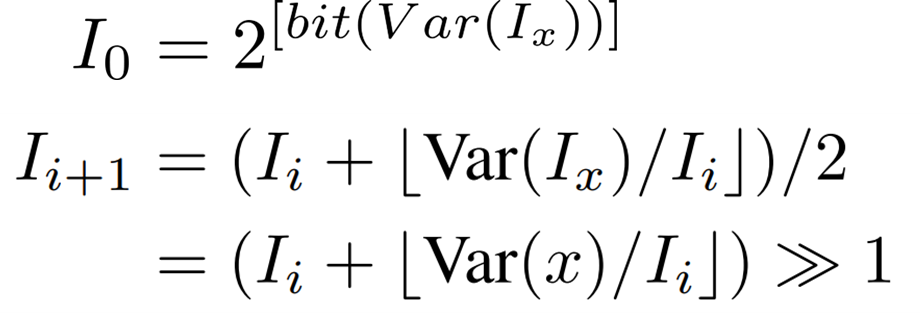
Experiment
Experimental procedure
To verify the superiority of I-ViT, we compare accuracy and latency on ImageNet (ILSVRC-2012), a large-scale classification task.
In addition to the FP baseline (without quantization), Faster Transformer and I-BERT are used for comparison. Also, ViT, DeiT, and Swim are used as models. Detailed settings are shown in Supplement [2].
Experimental results
The following table summarizes the results of the experiment. 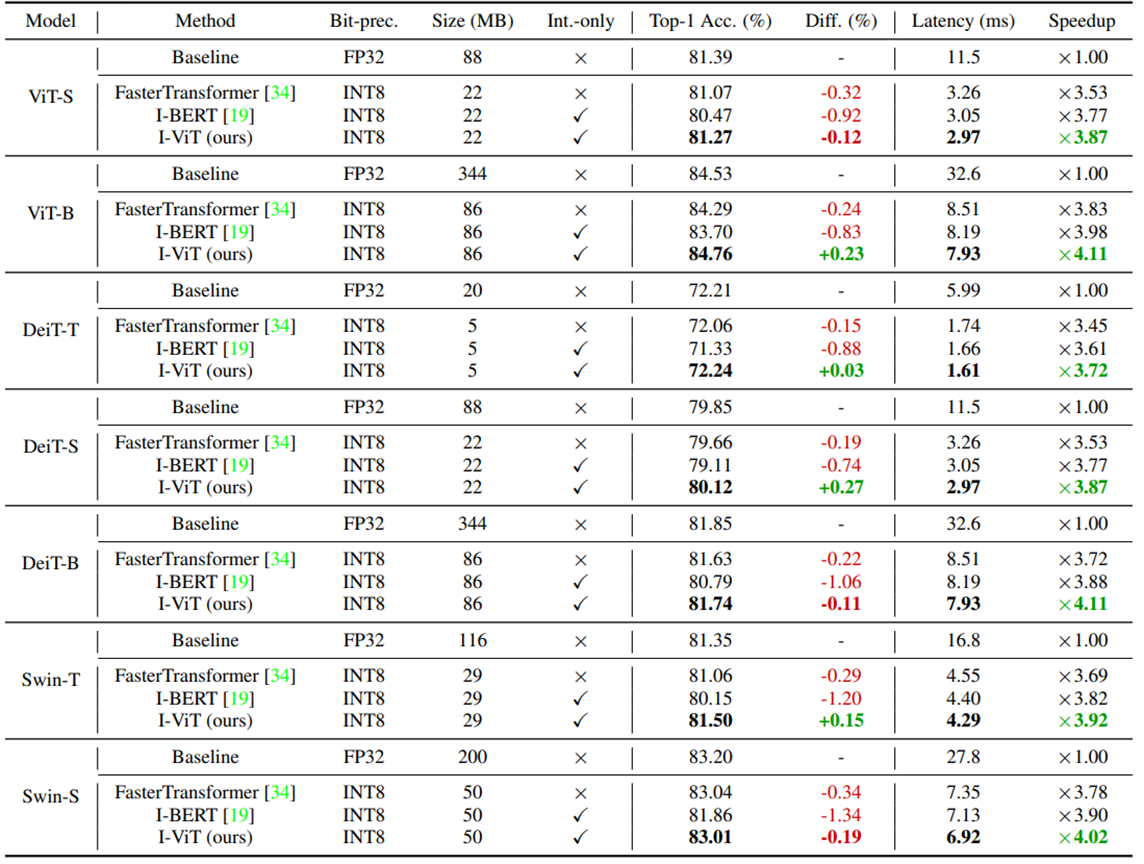
First, let's look at accuracy (Top-1 Acc.).
I-ViT showed similar or slightly better accuracy than FP baseline, with DeiT-S showing a 0.27% increase in accuracy.
It also outperformed FasterTransformer and I-BERT.
In particular, I-BERT lost 1.34% of its accuracy compared to FP baseline in Swim-S. This is due to the fact that I-BERT was developed for a language model, and the way it approximated it did not fit the image recognition task. This may be due to the fact that I-BERT was developed for a language model and its approximations did not fit the image recognition task.
Next, let's look at latency.
I-ViT achieved speedups of 3.72~4.11x, both higher than FasterTransformer and I-BERT.
The FasterTransformer processed the nonlinear operations as floating-point type, which may have resulted in inferior results compared to I-ViT.
In I-BERT, nonlinear operations are also performed with integer types, but I-ViT makes maximum use of hardware logic with bit shifting, which is thought to enable faster inference than in I-BERT.
Ablation Study
Experimental procedure
As an Ablation Study, we compare the accuracy and latency of replacing Shiftmax, ShiftGELU, and I-LayerNorm proposed in I-ViT with existing methods, respectively.
Shiftmax is compared to the squared polynomial approximation (Poly.) employed in I-BERT and LIS employed in FQ-ViT.
ShiftGELU is compared to the squared polynomial approximation (Poly.) used in I-BERT, and I-LayerNorm is compared to L1 LayerNorm used in Fully-8bit.
Experimental results
The following table summarizes the experimental results of the Ablation Study. 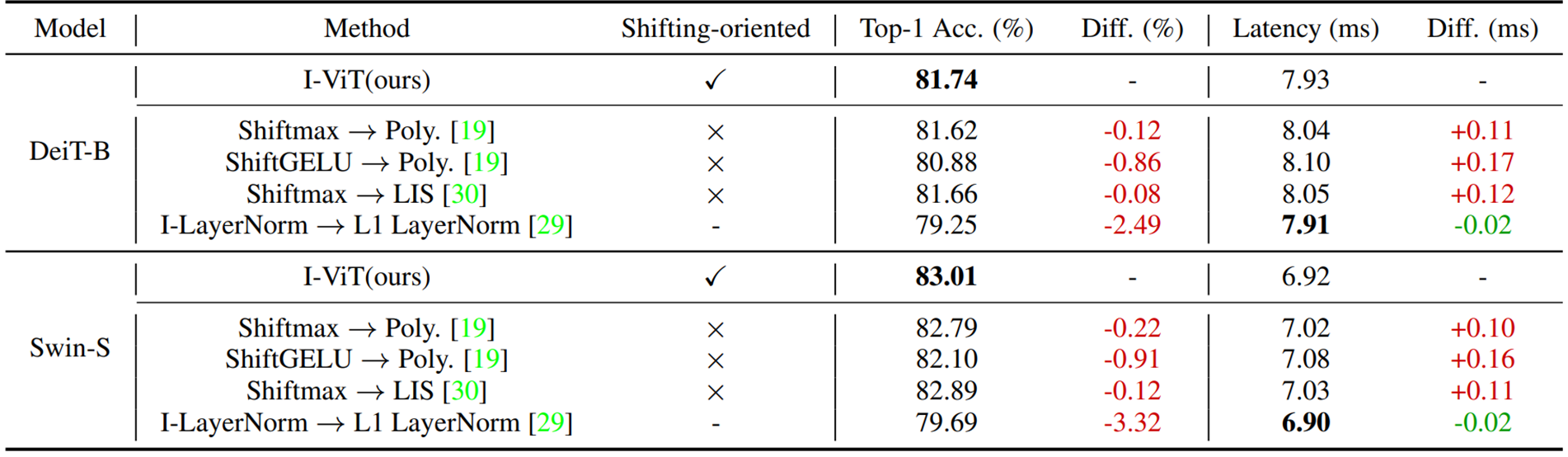
In both DeiT-B and Swin-S, replacing Shiftmax and ShiftGELU with the existing methods, respectively, results in lower accuracy and worse latency. In particular, the accuracy degradation is 0.86% and 0.96% for ShiftGELU→Poly. This result suggests that polynominal GELU, which approximates only a specific interval, is not well applied to ViT.
The reduction in speed can also be attributed to the fact that Shift-* makes more efficient use of hardware logic compared to the squared polynomial (Poly.) and LIS.
I-LayerNorm→L1 LayerNorm showed a significant deterioration in accuracy (2.49% and 3.32%) while latency was reduced by 0.02 ms.
Since L1 LayerNorm simplifies the calculation compared to I-LayerNorm, this result confirms that although it is faster, it does not maintain accuracy.
Summary
In this issue, we introduced i-ViT, a Vision Transformer that realizes all calculations in integer type.
As with I-BERT, the main attraction is that we were able to achieve a 3.72~4.11x increase in speed with almost no loss of accuracy.
Also, I-BERT used a squared polynomial approximation to compute Softmax and GELU in integer form, and I was wondering what would happen if Shiftmax and ShiftGELU, which are employed in I-ViT, were applied to the natural language processing model BERT.
In the future, highly accurate models will be able to be moved more easily.
Supplement
[1] Original paper on Vision Transformer: An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale
[2] Optimizer: AdamW
Learning rate: ( 2e-7, 5e-7, 1e-6, 2e-6) for tuning
batchsize: 8
GPU: RTX 2080 Ti
*Initially quantized learned weights FineTuning.
Categories related to this article




![[MusicLM] Text-to-Mu](https://aisholar.s3.ap-northeast-1.amazonaws.com/media/October2023/musiclm-520x300.png)



